Un tube de Coolidge est schématisé ci-dessous :


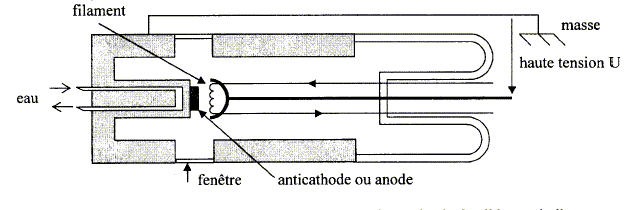
1. Rappeler le fonctionnement d'un tube de Coolidge en indiquant le rôle du filament, de la haute tension et de l'anticathode.
- Expliquer qualitativement en quoi le rendement énergétique proche de 1% de cet émetteur de rayonnement impose un refroidissement par eau.
Un vide poussé (environ 10 exposant -4 Pa) règne dans ce tube..
Les sont émis par un filament de tungstène chauffé par un courant électrique (effet ). Le filament joue le rôle de cathode. On établit entre la cathode et l'anode une tension élevée ; celle-ci les électrons émis par le filament. Les électrons accélérés frappent l'anode.
La plus grande partie de la puissance électrique (99 %) est dissipée sous forme de chaleur dans l'anode. Les tubes sont refroidits par une circulation d'eau.

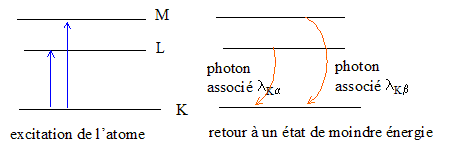
2. Spectre du rayonnement à la sortie du tube : le spectre d'émission est formé d'un fond continu sur lequel se superposent des raies d'émission intenses.
- Etude du fond continu : on admet que certains électrons sont arrêtés brutalement dans l'anticathode. Exprimer leur énergie cinétique E à l'arrivée sur l'anticathode en fonction de la haute tension U.
La vitesse initiale des électrons est négligeable ; le des électrons est négligeable devant la force électrique.
La seule force qui travaille est la force électrique : son travail est et vaut W= eU ( e : charge élémentaire)
Le théorème de l'énergie cinétique s'écrit : Ec finale - Ec départ= ½mv² -0= eU.

- En admettant que cette énergie est intégralement convertie en énergie de rayonnement X, montrer que la longueur d'onde X alors émise est donnée par : 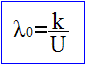. On exprimera k en fonction de h, c et e et on calculera sa valeur.
e= 1,60 10^-19 C ; h= 6,63 10^-34 J s ; c= 3,00 10^8 m/s
énergie du rayonnement X :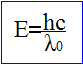
énergie cinétique des électrons : E= eU


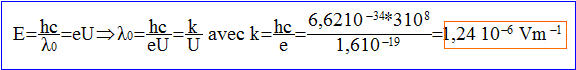
- Indiquer à quoi correspond 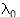sur le spectre d'émission. Préciser si cette caractéristique dépend du matériau de l'anticathode ; justifier.
En bombardant un solide à l'aide un faisceau d'électrons, on observe un freinage et une déviation des électrons dûs au champ électrique des noyaux de la cible.
Or une charge électrique dont la vitesse varie d'après les équations de Maxwel. Le freinage des électrons n'est pas quantifiée : les énergies des photons ne sont pas quantifiées ; le spectre en énergie est .
L'énergie maximale des photons X est égale à l'énergie cinétique initiale eU des électrons. Le spectre intensité = f( longueur d'onde) commence à partir de la valeu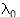r . Or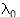 = hc/(eU) ; 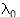ne dépend que de la tension accélératrice et en aucun cas de la nature de la cible.


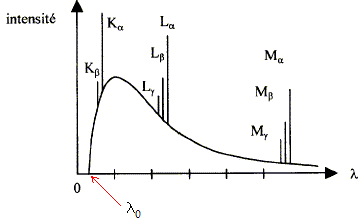
3. Etude du spectre de raies : à l'aide d'un diagramme énergétique représentant les niveaux d'énergie K, L, M d'un atome de l'anticathode, expliquer le processus physique en deux étapes qui génère les raies d'émission.
- Ces raies sont-elles caractéristiques du matériau de l'anticathode ? Justifier.
l'énergie de l'atome est : le spectre de raies est caractéristique des atomes constituant de l'anticathode.


- On fournit les valeurs des longueurs d'onde de raies X émises par un atome de cobalt :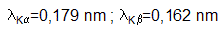 ainsi que l'énergie de liaison (eV) d'un électron situé sur la couche indiquée de l'atome de cobalt : couche K : 7,71 103 ; L : 765 ; M : 36,4. Justifier les valeurs des longueurs d'onde données ci-dessus à partir des énergies de liaisons de l'atome de cobalt.
l'énergie du phoiton X émis est égale à la d'énergie entre deux niveaux de l'atome :
transition L--> K : énergie du photon = 7710-765=6945 eV soit 6945*1,6 10^-19 = 1,111 10^-15 J.

transition M--> K : énergie du photon = 7710-36,4=7673,6 eV soit 7673,6*1,6 10^-19 = 1,228 10^-15 J.


4. Analyse cristallographique : on envoie un faisceau parallèle du rayonnement précédent de longueur d'onde 0,179 nm sur un cristal dont le réseau est cubique simple. On relève sur la figure de diffraction une raie d'ordre n=1 pour un angle de 15,5°. Cette raie correspond à la famille des plans réticulaires parallèles aux faces des mailles cubiques.

- Montrer que la loi de Bragg s'écrit dans ce cas :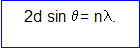
- Calculer le paramètre de la maille a.

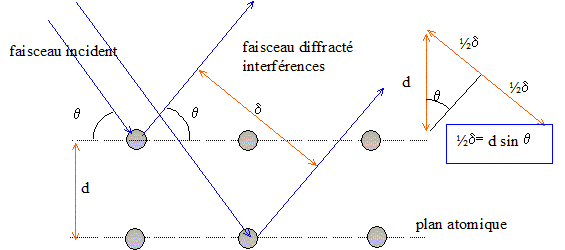
Chaque fois que la différence de marche 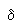est égale à un de la longueur d'onde, on observe une interférence .

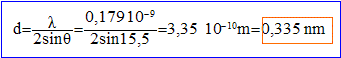
le paramètre de la maille cubique simple est égale à d.