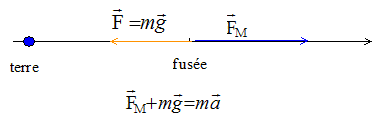Aurélie 28/04/06

Destination la Lune : d'après concours kiné Rennes ( physique) 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .


.
.


Destination la Lune (6 pts) 

Données : g0 = 9,8 m/s² ; RT= 6,4 103 km ; RL= 1,7 103 km

Une fusée de masse m se dirige vers la Lune. Ses occupants ont pour mission d'y déposer à sa surface des réflecteurs à rayon laser afin de pouvoir mesurer précisément la distance Terre- Lune.

I- En route vers la Lune : depuis la Terre des scientifiques suivent le déplacement de la fusée.

Position A : elle est située à hA= 8,0 103 km de la surface de la Terre et avance à la vitesse vA= 11 km/s

Position B : elle est située à hB= 1,0 104 km de la surface de la Terre et avance à la vitesse vB= 13 km/s

  1. Exprimer en fonction des données, la valeur g du champ de gravitation crée par la Terre, à une altitude h, dans la position A puis dans la position B. Faire les application numérique.
    Dans la suite de l'exercice, on supposera que ce champ de gravitation varie peu entre les positions A et B ; il sera pris égal à la moyenne des deux valeurs trouvées. On négligera l'attraction gravitationnelle de la Lune.
  2. La fusée est suposée se dirigée sur une droite reliant le centre de la Terre et le centre de la Lune. La force motrice du moteur de la fusée est modélisée par une force constante de valeur FM.
    - Représenter sur un schéma les forces s'exerçant sur la fusée entre les positions A et B
    - Déterminer l'expression littérale de la valeur FM de la force motrice.
    - Déterminer l'expression littérale de la valeur a de l'accélération de la fusée entre les deux positions A et B. Faire l'application numérique.
    - Comparer l'accélération d'un membre de l'équipage à celle de la fusée. L'équipage flotte-t-il dans la cabine ? Justifier.

II- Sur la Lune : ils déposent plusieurs réflecteurs sur la Lune. Depuis la Terre les scientifiques visent l'un des réflecteurs à l'aide d'un faisceau laser et mesure la durée Dt= 2,51 s séparant l'émission de la réception. Déterminer la distance séparant les centres des deux astres.

corrigé
valeur g du champ de gravitation crée par la Terre, à une altitude h :

à la surface de la Terre g0 = GMT/RT² soit GMT = g0RT²

à l'altitude h : g = GMT/(RT+h)² = g0RT² /(RT+h)² = g0/ ( 1+h/RT)²

gA= 9,8 / ( 1+ 8/6,4)² = 1,94 m/s².

gB= 9,8 / ( 1+ 10/6,4)² = 1,49 m/s².

valeur moyenne : g=(gA+gB)/2 = 1,71 m/s².

forces s'exerçant sur la fusée entre les positions A et B :

expression littérale de la valeur FM de la force motrice : FM= m(a+g)

d'autre part : v²B-v²A= 2AB a soit a= (v²B-v²A)/(2AB) ;

vA= 11 103 m/s ; vB= 13 103 m/s ; AB= hB-hA = 2 106 m ; a = (13²-11²)106 / (2* 2 106) = 12 m/s².

d'où FM =m ((v²B-v²A)/(2AB) +g)

l'accélération d'un membre de l'équipage à identique à celle de la fusée : en mouvement rectiligne accéléré, les membres de l'équipage sont plaqués contre leurs sièges.

distance séparant les centres des deux astres :

distance séparant les surface des deux astres : aller + retour = c Dt avec c = 3 108 m/s, vitesse de la lumière dans le vide.

aller = retour =½ c Dt = 0,5*3 108*2,51 = 3,76 108 m = 3,76 105 km

ajouter les rayons des deux astres : 3,76 105 + 6,4 103 + 1,7 103 = 3,84 105 km.

retour -menu