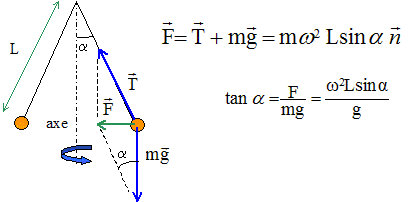|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
||
| .
. |
||
|
||
|
|
Données : g= 10 m/s² ; constante de Plank : h = 6,63 10-34 J s ; c= 3 108 m/s ; e = 1,6 10-19 C ; NA= 6 1023 mol-1. La force de frottement qui s'exerce sur un objet de section S se déplaçant dans l'air à une vitesse v est donnée par la relation : f= ½CxrSv² où r =1,3 kg m-3 est la asse volumique de l'air et Cx un coefficient qui dépend de la forme d'e l'objet. Si une boule sphérique, de masse m=90 g et de rayon r= 4 cm, tombe verticalement dans l'air, sa vitesse, est au bout de quelques secondes, constante et vaut 25 m/s.
corrigé Le mouvement étant rectiligne uniforme, le poids compense la force de frottement : mg = ½CxrSv² Cx = 2mg / (rSv²) avec S= pr² = 3,14 *0,04² = 5,024 10-3 m² ; v = 25 m/s ; r =1,3 kg m-3 ; m = 0,09 kg ; g= 10 m/s² Cx = 2*0,09*10 / ( 1,3 * 5,024 10-3
* 25²) = 0,44.
analyse dimendionnelle : mg a la dimension d'une force ou dune masse fois une accélération : M L T-2. [r ] = M L-3 ; [S]= L2 ; [v²]= L2 T-2 d'où [rSv²] =M L T-2 par suite : [Cx ] est sans dimension et sa valeur est inchangée dans le système cgs.
|
|
|
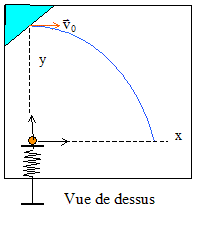
Un jeu de billes rudimentaire est composé d'une planche rectangulaire inclinée à p/6 rad par rapport à l'horizontale dont les 4 côtés sont pourvu d'un montant et d'un lanceur dans l'angle inférieur gauche. Le lanceur consiste en un axe parallèle à la planche avec une rondelle à chaque extrémité. La rondelle inférieure se trouve à l'extérieur du montant que l'axe traverse. On peut tirer sur la rondelle extérieure afin de comprimer un ressort dont l'axe occupe la parite centrale et dont les extrémités sont fixées à la rondelle supérieure et l'autre à la partie intérieure du montant. La bille est placée au contact de la rondelle supérieure. Le joueur tire lentement sur la rondelle inférieure ( la bille restant au contact de la rondelle supérieure) jusqu'à racourcir le ressort de 5 cm, puis lâche brusquement la rondelle inférieure. La bille roule alors vers le haut de la planche selon un ligne de plus grande pente. La masse de la bille est de 50 g ; celles du ressort, des rondelles et de l'axe sont négligeables devant la masse de la bille. La raideur du ressort es de 100 N/m et on néglige les frottements. On prend pour origine le point où se trouvait la bille au moment où elle quitte le ressort du lanceur, l'horizontale passant par ce point est appelé " ligne de lâcher ".
corrigé distance parcourue par la bille sur la planche poursuivant son parcours rectiligne vers le haut selon la plus grande pente avant de retomber : Initialement l'énergie du système {bille ressort }est sous forme potentielle élastique : ½kx² = 0,5*100*0,05² =0,125 J Au moment du lâcher cette énergie est convertie en énergie cinétique emportée par la bille : ½mv² = 0,125 J Lors de la montée l'énergie cinétique initiale est convertie en énergie potentielle de pesanteur : mgh mghmax = 0,125 ; hmax = 0,125 / (mg) =0,125 / (0,05*10) =0,25 m Distance parcourue sur la planche : hmax
/ sin (p/6) = 0,50 m = 50 cm.
calcul de la valeur de la vitesse v0 : après un parcours de 0,4 m sur la planche, l'énergie initiale de la bille se trouve sous forme cinétique et sous forme potentielle de pesanteur : 0,125 = mgh + ½mv²0 ; v²0 =0,25/ m- 2gh avec h = 0,4 sin(p/6) = 0,2 m et m = 0,05 kg v²0 = 0,25/0,05-2*10*0,2 =1 ; v0 = 1 m/s. trajectoire de la bille dans le repère ci-dessus : vecteur accélération : (0 ; - gsin (p/6) = -5 ) vecteur vitesse initiale : ( 1 ; 0 ) ; position initiale ( 0 ; 0,4) vecteur vitesse à la date t, primitive du vecteur accélération : ( 1 ; -5 t ) vecteur position , primitive du vecteur vitesse : x= t ; y = -2,5 t² + 0,4 trajectoire ( éliminer le temps entre ces deux relations) : y = -2,5 x² + 0,4 abscisse du passage à la "ligne de lâcher" : y= 0 soit -2,5 x² + 0,4 = 0 x² = 0,4 / 2,5 = 0,16 ; x = 0,4 m.
|
||
|
Un régulateur à boules est schématisé ci-dessous. Deux boules de même masse m=50 g, placées de part et d'autre d'un axe vertical tournant lui sont reliés par deux barres mobiles dans un plan vertical. L'angle entre les deux barres et l'axe est donc variable, sensiblement nul lorsque l'axe ne tourne pas. La longueur d'une barre entre son attache au niveau de l'axe et le centre d'inertie d'une boule est de 20 cm. 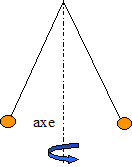
corrigé vitesse angulaire de l'ensemble lorsque les boules font un angle de p/3 rad avec la verticale :
w² = g tan(p/3) / (L sin (p/3 )) =g / (Lcos (p/3 ))= 10 / (0,2 cos 60) =100 ; w = 10
rad/s.
Energie cinétique initiale du dispositif : ½(2m) v² = m w²L² sin² (p/3 ) énergie dissipée par le couple de freinage : f r q avec q angle dont tourne le système en radian et r : rayon de l'axe = 1,5 10-3 m. m w²L² sin² (p/3 ) = f r q m w²L²sin² (p/3 )= f rq ; q = m w²L²sin² (p/3 )/( f r)= 0,05*100*(0,2 sin 60)² / (1,5*1,5 10-3) =66,7 rad or un tour correspond à 6,28 rad, d'où le nombre de tours : 66,7 / 6,28 = 10,6 tours.
|
||
|
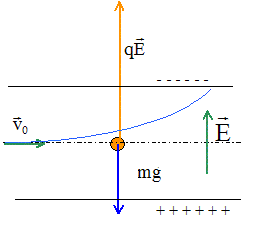
Des particules de masse m et de charge positive +q sont projetés dans le vide. Elles entre avec une vitesse horizontale entre les armatures horizontales d'un condensateur de capacité C. L'une des armatures est à la hauteur zéro et l'autre, au dessus, à la hauteur d.
corrigé 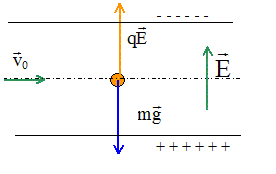
trajectoire horizontale de vitesse constante : mouvement rectiligne uniforme le poids des
particules compense la force électrique auquelle sont soumises les
particules : qE=mg soit E=
mg/q.
|
||
|
On étudie les oscillations électriques forcées d'un circuit branché aux bornes d'un générateur de tension de fréquence f variable. La tension efficace est de 100 V. Ce circuit comporte une bobine de résistance r= 50 W en série avec un condensateur de capacité C= 1 mF. L'intensité efficace du courant dans le circuit prend une valeur maximale pour une fréquence f= 200 Hz.
corrigé A la résonance d'intensité LCw² = 1 avec w = 2pf = 2*3,14*200 = 1256 rad/s et C = 10-6 F. d'où L= 1/(Cw² ) = 1/(10-6*1256²)
= 0,63 H.
de plus l'intensité efficace s'exprime par : I= U/Z = 100 / 50 = 2 A. L'intensité est maximale à la résonance donc [c) et d) vrais ; a) et b) faux] La bande passante à 3 dB correspond dans ces conditions à l'intervalle des fréquences pour lesquelles l'intensité efficace est supérieure à l'intensité maximale divisée par racine carrée de 2 soit 1,4 A vrai.
|
||
|
|