|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Partie 1 : chute libre dans l'air ( frottement et poussée d'Archimède négligés) A la date t=0 la balle est abandonnée sans vitesse initiale et le centre d'inertie est en O. Le mouvement a lieu suivant l'axe vertical Oz, orienté vers le bas.
Partie 2 : chute avec frottement dans un bain d'huile. La balle est placée dans une grande éprouvette pleine d'huile et on recommence l'expérience précédente. Les frottements sont assimilés à une force de valeur f=kv, colinéaire et de sens contraire à la vitesse où k est une constante. On obtient la courbe suivante représentant les variations de la vitesse au cours du temps : 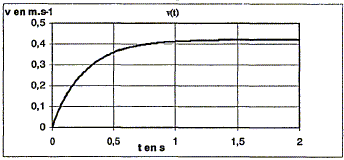
Partie 3 : détermination du coefficient de viscosité. Pour des vitesses faibles la valeur de la force de frottement est f = 6phR v où h est le coefficient de viscosité de l'huile.
corrigé Partie 1 : chute libre dans l'air ( frottement et poussée d'Archimède négligés) A la date t=0 la balle est abandonnée sans vitesse initiale et le centre d'inertie est en O. Le mouvement a lieu suivant l'axe vertical Oz, orienté vers le bas. Bilan des forces appliquées à la balle : La chute étant libre, la balle n'est soumise qu'à son poids, vertical, vers le bas, valeur mg. Equation différentielle du mouvement du centre d'inertie de la balle : La seconde loi de Newton s'écrit, sur l'axe z : mg = md²z/dt² ; d²z/dt² = g. Equation horaire du mouvement z=f(t) : la vitesse est une primitive de l'accélération : v(t) = gt + v0 avec v0 = 0 dans ce cas. l'abscisse est une primitive de la vitesse : z(t) = ½gt²+ h0 avec h0 = 0 dans ce cas. Temps nécessaire pour atteindre l'abscisse z1 = 80 cm = 0,8 m t²= 2z1 / g = 1,6 / 9,81 = 0,163 ; t = 0,40 s. Valeur de la
vitesse v1 de la balle : v1
= 9,81*0,40 = 3,96 ( 4,0
m/s)
La balle est placée dans une grande éprouvette pleine d'huile et on recommence l'expérience précédente. Les frottements sont assimilés à une force de valeur f=kv, colinéaire et de sens contraire à la vitesse où k est une constante. On obtient la courbe suivante représentant les variations de la vitesse au cours du temps :
La vitesse limite notée vL vaut 0,42 m/s d'après le graphe. Elle est atteinte à t = 1 s. Equation différentielle vérifiée par la vitesse :
Ecrire la seconde loi de Newton sur l'axe Oz, vertical, orienté vers le bas : P-F-Pa = md²z/dt² = mdv/dt P= mg ; F= kv ; Pa = rhuilegV avec V : volume de la balle V = 4/3*3,14 * 23 = 33,5 mL mg - kv - rhuilegV = dv/dt ; dv/dt + k/ m v = g(1- rhuileV/m) dv/dt + av = b avec a et b constantes a = k/m = 0,136 / 36 10-3 = 3,8 s-1. b= g(1- rhuileV/m)= 9,81(1-0,9*33,5 / 36) = 1,6 m s-2. Vérifions que v(t) = vL(1-exp(-at)) est solution de cette équation différentielle : dv/dt = vLaexp(-at) puis repport dans l'équation différentielle. vLaexp(-at) + avL(1-exp(-at)) = avL Or lorsque la vitesse limite est atteinte , dv/dt = 0 soit avL = b d'où vLaexp(-at) + avL(1-exp(-at)) = b Calcul de
vL : vL = b / a
=1,6 / 3,8 = 0,42 m/s, en accord avec la valeur lue sur le graphique.
Pour des vitesses faibles la valeur de la force de frottement est f = 6phR v où h est le coefficient de viscosité de l'huile. Influence de h sur vL : si la viscosité augmente, la force de frottement augmente et la vitesse limite est plus rapidement atteinte. De plus vL = b / a =g(m- rhuileV) /k = g(m- rhuileV) / (6phR) si la viscosité augmente, la vitesse limite diminue. Expression de h en fonction de vL, g, R et rhuile : vL =g(m- rhuileV) / (6phR) ; h = g(m- rhuileV) / (6pvLR) Calcul de h = (36-0,9*33,5)10-3*9,81 /(0,42*6*3,14 *0,02) = 0,36 kg m-1 s-1. Retrouver le résultat précédent en calculant h à partir de k : k = 6phR = 0,136 d'où : h =0,136 / (6pR) = 0,136 / (6*3,14*0,02 )= 0,36 kg m-1 s-1.
|
|
|
Partie 1 : résistance négligeable 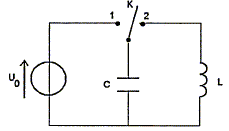 Le condensateur de capacité C= 0,1 mF est chargé sous une tension U0 = 12 V. La charge étant terminée, à la date t=0 on décharge le condensateur dans une bobine d'inductance L= 1,0 H, de résistance négligeable. La résistances des fils de jonction est aussi négligeable.
Partie 2 : étude du circuit réel. L'étude du circuit laisse apparaître un amortissement.
corrigé Partie 1 : résistance négligeable
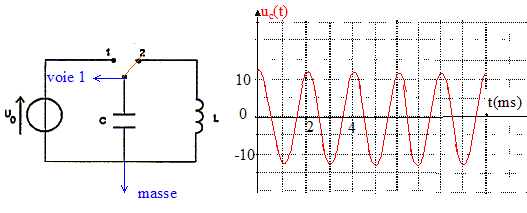
Le condensateur de capacité C= 0,1 mF est chargé sous une tension U0 = 12 V. La charge étant terminée, à la date t=0 on décharge le condensateur dans une bobine d'inductance L= 1,0 H, de résistance négligeable. La résistances des fils de jonction est aussi négligeable. On ferme l'interupteur en position 1 pour charger le condensateur. En fin de charge la tension aux bornes du condensateur est U0 ; l'énergie stockée est EC= ½CU0². A la date t=0, pour décharger le condensateur dans la bobine, on bascule l'interrupteur en position 2. Equation différentielle vérifiée par uc(t) : tension aux bornes de la bobine Ldi/dt avec i = dq/dt ; di/dt = d²q/dt² de plus q= Cuc(t) d'où d²q/dt² = Cd²uc/dt² additivité des tensions uc(t) + Ldi/dt = 0 ; uc(t) + LCd²uc/dt² = 0. Vérifions que uc(t) = U0 cos (2pt/T) est solution de cette équation : dériver : duc(t) /dt = U02p/T (-sin (2pt/T)) dériver une seconde fois : d²uc/dt² = - U0(2p/T)² cos (2pt/T) repport dans l'équation différentielle : U0 cos (2pt/T) - LCU0(2p/T)² cos (2pt/T) =0 expression vérifiée quel que soit t si LC(2p/T)² = 1. Expression de T, période : T² = 4p²LC
soit T =2p (LC)½. EL= ½LI² soit L = 2EL/I² ; L a la dimension d'une énergie divisée par une intensité au carré EC= ½CU² soit C = 2EC/ U² ; C a la dimension d'une énergie divisée par une tension au carré. (LC)½ a la dimension d'une énergie divisée par le produit ( intensité fois tension) or une intensité fois une tension est une puissance, ou encore une énergie divisée par un temps. en conséquence (LC)½ a la dimension d'un temps. Calcul de T : 2*3,14 ( 1*10-7)½ = 1,98 10-3 s ( 2,0 10-3 s) On visualise la tension uc(t) à
l'aide d'un oscilloscope à mémoire. ( sensibilités : 1 ms/div ; 5V/div) Expressions des énergies EC et EL emmagasinées respectivement dans le condensateur et dans la bobine à chaque instant : EC = ½Cu² = ½CU20 cos2 (2pt/T) EL = ½Li² avec i (t) = dq/dt = C duc/dt = CU02p/T (-sin (2pt/T) EL = ½LC2U20 (2p/T)2sin2 (2pt/T) or (2p/T)2
=1/(LC) d'où : EL = ½CU20sin2
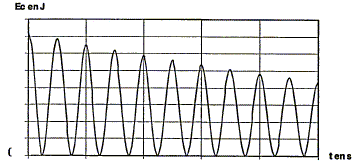
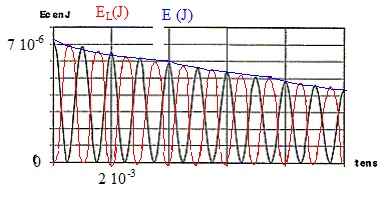
(2pt/T) E = 0,5* 10-7*12² = 7,2 mJ Partie 2 : étude du circuit réel. L'étude du circuit laisse apparaître un amortissement. Cet amortissement se répercute sur le graphe représentant uc(t) : l'amplitude de la tension diminue au cours du temps Une partie de l'énergie est dissipée sous forme de chaleur ( effet joule) lors des échanges d'énergie entre condensateur et bobine.
Les énergies sont proportionnelles soit au carré du cosinus ou du sinus : donc leur période est ½T.
|
||
|
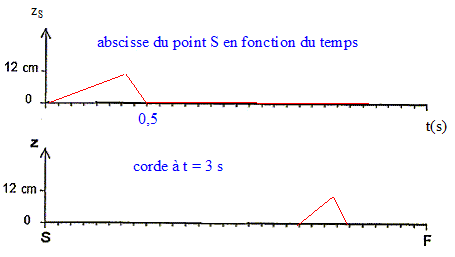
Partie 1 : propagation d'une perturbation Une longue corde élastique de longueur L=SF= 6,0 m est initialement reposée sur le sol horizontal. La corde est légèrement tendue : le point F est fixe, le point S à l'autre extrémité est tenu à la main par un opérateur qui cré à la date t=0s, une perturbation en déplaçant rapidement le point S horizontalement dans la direction perpendiculaire à la corde, puis en la ramenant aussitôt à sa position initiale. La durée de cette perturbation est Dt = 0,50 s. On représente les aspects de la corde à deux dates différentes : 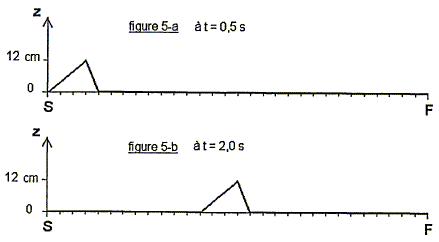
Partie 2 : influence de quelques paramètres.
corrigé Partie 1 : L''onde qui prend naissance après cette perturbation est une onde progressive transversale : sa direction de propagation est perpendiculaire à la direction de la déformation. Célérité de l'onde : d'après les graphes, en 0,5 s la perturbation parcours
0,8 m d'où v= 0,8/0,5 = 1,6
m/s. Soit A un point de la corde tel que SA= 2,0 m. Le
mouvement du point A reproduit le mouvement de la source avec le retard
q = AS/v = 2/1,6 =
1,25 s.
L'oprérateur recommence l'expérience, dans les mêmes conditions, mais avec un geste plus lent : Dt'= 0,70 s. La célérité de l'onde n' est pas modifiée : elle dépend des caractéristiques du milieu de propagation. On rappelle que la célérité d'une onde se déplaçant le
long d'une corde est donnée par v= (T/m)½
où T représente la tension de la corde en newton et m la masse linéique en kg m-1. La célérité de l'onde est modifiée : la célérité est proportionnelle à la racine carrée de la tension T ; si la tension double, la célérité est multipliée par 2½. Calcul de la masse linéique de la corde : m = masse (kg) / longueur (m) =0,3 / 6 = 5,0 10-2 kg m-1. La célérité est modifiée si on utilise, dans les mêmes conditions que dans l'expérience de la partie1, une corde de même longueur mais de masse deux fois plus élevée : la célérité est inversement proportionnelle à la racine carrée de la masse linéique ; si la masse linéique double, la célérité est divisée par 2½.
|
||
|
|