|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
On étudie le mouvement d'unsatellite de la Terre dans le référentiel géocentrique. On admet que le satellite est à symétrie sphérique de masse m et que le mouvement de son centre d'inertie est circulaire uniforme, le rayon de cette trajectoire est noté R.
La troisième loi de Kepler : On appelle satellite à basse altitude un satellite dont on peut négliger l'altitude h devant le rayon de la Terre.
Satellisation : On se propose d'étudier les conditions optimales de lancement d'un satellite à basse altitude.
masse de la terre MT= 5,98 1024 kg ; rayon de la Terre RT= 6380 km ; G= 6,67 10-11 N kg-2 m2 ; jour sidéral TS= 23 h 56 min. corrigé Définition du référentiel géocentrique : le référentiel est la Terre. L'origine du repère est le centre de la Terre et les trois axes pointent vers des étoiles lointaines qui paraissent fixes. L'étude des satellites est simple dans le référentiel géocentrique, fixe par rapport à la Terre : un référentiel terrestre est en mouvement par rapport à la Terre et ne peut convenir pour cette étude. Valeur de la force de gravitation à laquelle est soumise le satellite sur son orbite circulaire : Le satellite n'est soumis qu'à la force de gravitation centripète ; cette force est à chaque instant perpendiculaire à la vitesse et en conséquence sa puissance est nulle. L'énergie cinétique du satellite ne varie pas : donc la valeur de la vitesse est constante ( mouvement uniforme). Expression de la vitesse v et la période T de ce satellite en fonction de G, M, R, h : le satellite est soumis à la seule force de gravitation centripète exercée par la planète
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/ (R+h) d'où la valeur de la vitesse (m/s): v² =GM / (R+h). indépendante de la masse du satellite Enoncé de la deuxième loi de Newton : Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie. La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (RT+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (RT+h) ² = v² T² = GMT/ (RT+h) T² ou T² =4p² /(GMT)(RT+h)3. soit T² /(RT+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg. Calcul de k : k= 4*3,142/(6,67 10-11 *5,98 1024) =9,89 10-14 s2 m-3. La troisième loi de Kepler : On appelle satellite à basse altitude un satellite dont on peut négliger l'altitude h devant le rayon de la Terre.
Spot : T2 = (101*60)2=3,67 107 s² ; R3 = (7,2 106)3 = 4,39 1020 m3 ; T2/R3 = 9,83 10-14. Météostat : T2 = (1430*60)2=7,36 109 s² ; R3 = (4,21 107)3 = 7,46 1022 m3 ; T2/R3 = 9,86 10-14. Spot et Météostat vérifient la troisième loi de Kepler. Déduction de la valeur de k : 9,84 10-14 Comparaison à celle de la question précédente : l'écart relatif est de 100*(9,89-9,84)/9,89 = 0,5%. Période d'un satellite de basse altitude : T² = kR3 = 9,89 10-14 * (6,38 106)3 = 2,57 107 s² ; T= 5,07 103 s = 84,5 min rayon de l'orbite (km) d'un satellite géostationnaire : R3 = T²/k = (1436*60)² / 9,89 10-14 = 7,5 1022 ; R= 4,22 107 m. Définition d'un satellite géostationnaire : ils tournent dans le plan équatorial, dans le même sens que la Terre, et avec la même vitesse angulaire que la Terre. Ils paraissent fixes pour un observateur terrestre. Satellisation : On se propose d'étudier les conditions optimales de lancement d'un satellite à basse altitude. Le sens de rotation de la Terre : la Terre est en rotation d'Ouest vers l'Est. Vitesse v0 d'un point de la surface de la Terre situé à l'équateur : vitesse angulaire W= 6,28 / (24*3600) = 7,3 10-5 rad/s. La vitesse linéaire transmise par la Terre à un corps lancé depuis sa surface est : à l'équateur : v = W RT = 7,3 10-5 * 6,37 106 = 463 m/s. Ce vecteur vitesse est tangent à la Terre et dirigé vers l'Est. La vitesse du satellite avant le décollage du lanceur chargé de le placer en orbite vaut 463 m/s. La vitesse du satellite placé en orbite est : v² =GM / RT. v²= 6,67 10-11 * 5,98 1024 / (6,38 106) = 6,25 107 ; v= 7,9 103 m/s.
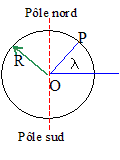
Le satellite S a été lancé à partir d'une base terrestre située à la latitude l d'un point P à la surface de la Terre. La vitesse linéaire transmise par la Terre à un corps lancé depuis sa surface est : à l'équateur : v = W R = 7,3 10-5 * 6,37 106 = 463 m/s. à la latitude l = 28°N : vl= W R cos l = 7,3 10-5 * 6,37 106 cos 28 = 409 m/s. Une base de lancement proche de l'équateur conduit à une vitesse initiale de lancement plus grande que celle d'un site situé à une latitude supérieure. Cela est un énorme avantage : cette vitesse additionnée vectoriellement avec la vitesse de la fusée porteuse, détermine la vitesse finale du satellite.
|
||||||||||||||||||||||||||||||||||||||||||
|
Un rayon laser de longueur d'onde dans le vide l= 633 nm, traverse une fente verticale de largeur a. Un écran vertical est placé à une distance D= 1,50 m de la fente perpendiculairement à la direction du laser.
corrigé Un rayon laser de longueur d'onde dans le vide l= 633 nm, traverse une fente verticale de largeur a. Un écran vertical est placé à une distance D= 1,50 m de la fente perpendiculairement à la direction du laser. Limites de longueurs d'onde dans le vide du spectre de la lumière blanche : 400 nm ; 800 nm. Couleur est la lumière émise par le laser : 633 nm donc jaune orangé. Schéma du dispositif : le laser éclaire la fente.
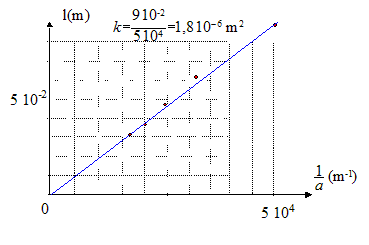
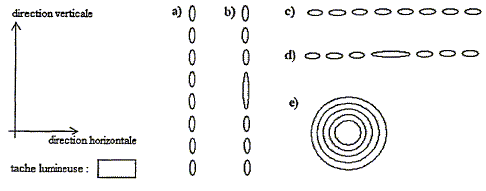
l'expression de l en fonction de a : l = 1,8 10-6(1/a).
Expression traduisant correctement le résultat précédent
: On remplace la fente précédente par un cheveux vertical. On obtient une tache centrale de largeur l =2,6 cm. Le diamètre du cheveux : l = 1,8 10-6(1/a) soit a = 1,8 10-6 / l = 1,8 10-6 / 0,026 = 6,9 10-5 m = 69 mm.
|
|||||||||||||||||||||||||||||||||||||||||||
|
On réalise un circuit série comprenant un générateur de tension de fem E=6,0 V, un conducteur ohmique de résistance R= 1,0 kW, un condensateur de capacité C= 10 mF et un interrupteur K. A l'instant t=0 le condensateur est déchargé et on ferme K.
corrigé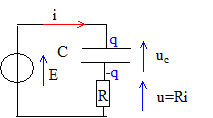 
relation entre la tension uc aux bornes du condensateur et la charge q : q= Cuc. Equation différentielle vérifiée par la tension uc : additivité des tensions : uc+Ri = E ; de plus i = dq/dt = Cduc/dt. d'où : uc + td uc/dt = E où t =RC est la constante de temps du circuit. Montrons que la constante de temps est homogène à un temps : R est une résistance soit une tension divisée par une intensité ; C est une capacité soit une charge divisée par une tension ; de plus une charge est une intensité fois un temps d'où t a
la dimension d'un temps.
duc = uc(t +dt ) - uc(t ) soit : uc(t +dt ) = uc(t ) + duc (1) l'équation différentielle donne : td uc/dt = E -uc d uc =( E -uc )dt / t (2) d uc =( E -uc )dt / t (2) avec dt / t = 10-4 / (1000 * 10-5) =0,01. (2) donne : d uc =( 6 -0)*0,01 = 0,06 V ; (1) donne : uc(1)=uc(0)+d uc = 0,06 V (2) donne : d uc =( 6 -0,06)*0,01 = 5,94 10-2 V ; (1) donne : uc(2)=uc(1)+d uc = 0,06 +5,94 10-2 =11,9 10-2 V (2) donne : d uc =( 6 -11,9 10-2)*0,01 = 5,88 10-2 V ; (1) donne : uc(3)=uc(2)+d uc = 11,9 10-2 +5,88 10-2 =17,8 10-2 V (2) donne : d uc =( 6 -17,8 10-2)*0,01 = 5,82 10-2 V ; (1) donne : uc(4)=uc(3)+d uc = 17,8 10-2 +5,82 10-2 =23,6 10-2 V (2) donne : d uc =( 6 -23,6 10-2)*0,01 = 5,76 10-2 V ; (1) donne : uc(5)=uc(4)+d uc = 23,6 10-2 +5,76 10-2 =29,4 10-2 V
la courbe uc(t) = f(t)
La constante de temps déterminée par calcul est identique à la valeur calculée.
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
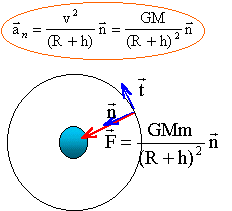
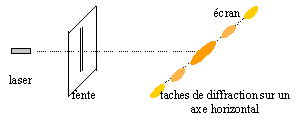
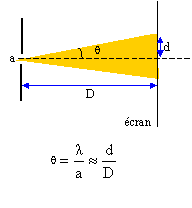soit d = lD/a ou l =2d = 2lD/a 