|
onde sonore, satellite géostationnaire, radium, oscillateur mécanique vertical, mouvement uniformément varié, circuit rLC En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Un diapason émet quand on le trappe la note La 3 que l'on considérera comme un signal sinusoïdal de fréquence 440 Hz.
corrigé L'onde sonore est une onde longitudinale : la perturbation ( variation de pression) se propage dans la direction de propagation de l'onde. période T (s) = 1/fréquence (Hz) = 1/440 = 2,27 10-3 s = 2,27 ms. La fréquence caractérise l'onde. La célérité (m/s) dépend du milieu : température et pression ont une influence sur la célérité du son dans l'air. longueur d'onde l(m) = célérité (m/s) / fréquence (Hz) = 343,9 / 440 = 7,82 10-1 m.
|
|
|
Au cours d'une future mission, on envisage de placer un satellite géostationnaire autour de Mars. On donne pour cette planète : masse: M = 6,42 l023 kg ; rayon équatorial: R =3 398 km ; période de rotation sidérale (temps de révolution sur elle même) : 24,62 h ; constante de gravitation universelle: G = 6,67 10-11SI. Calculer l'altitude du satellite. corrigé Un satellite géostationnaire tourne dans le plan équatorial de Mars, dans le même sens et avec la même vitesse angulaire . La période du satellite est égale à la période de Mars soit T= 24,62*3600 = 8,863 104 s. La 3éme loi de Kepler s'écrit : T2 / r3 = 4p²/(GM) où r : distance (m) du centre de mars au satellite r3 = T2GM/(4p²) = (8,863 104 )2 *6,67 10-11*6,42 l023 / (4*3,14²) = 8,53 1021 m3. prendre la racine cubique r = 2,043 107 m = 2,043 104 km Pour obtenir l'altitude, retrancher le rayon de Mars : 2,043 104 -3 398=1,70 104 km.
|
||
|
Le radium donne du radon par désintégration a.
On donne : l'unité de masse atomique u : 1,6605 10 27kg ; la masse du noyau du radium Ra : 225,9771 u ; la masse du noyau de radon Rn : 221,9704 u ; la masse d'une particule a : 4,0015 u ; l'équivalent masse énergie pour une unité atomique Eu = 931,4942 MeV sachant que 1eV= 1,6022 10-19J. corrigé 22688Ra --> 22286Rn + 42He énergie de masse du noyau de radium : 225,9771*931,4942 =2,104963 105 MeV énergie de masse du noyau de radon : 221,9704 *931,4942 =2,067641 105 MeV énergie de masse du noyau d'hélium : 4,0015 *931,4942 =3,72737 103 MeV énergie libérée au cours de la réaction : 2,105 105 -(2,0676 105+3,7274 103)= 4,843 MeV soit 4,843 106 eV ou 4,843 106 *1,6022 10-19 = 7,760 10-13 J. Cette énergie est emportée par la particule a sous forme d'énergie cinétique. Si les noyaux fils sont dans un état exité, ils libèrent de l'énergie sous forme d'un photon g.
|
||
|
L'extrémité supérieure d'un ressort vertical idéal, à spires non jointives de longueur à vide l0, de coefficient de raideur k, est fixée à un support. Un solide de masse m est accroché à l'autre extrémité.
corrigé référentiel terrestre supposé galiléen. Le solide suspendu à l'extrémité du ressort est soumis à : son poids, vertical, vers le bas, valeur P=mg la tension du ressort, verticale, vers le haut : T= k(le-l0) A l'équilibre la somme vectorielle de ces deux forces est nulle : k(le-l0) +mg =0(1) (1)
donne : k(le-l0)
= mg soit le = l0 + mg/k
Ecrire la deuxième loi de Newton sur cet axe : mg-k (le+z -l0) = m z" en tenant compte de (1)
: z" + k/m z = 0 on pose w20
= k/m ( w0 : pulsation en
rad/s)
|
||
|
Une grue portuaire soulève verticalement une charge de masse M = 10 tonnes, par l'intermédiaire d'un câble de masse négligeable, en un lieu où l'accélération de la pesanteur g = 9,81 m.s-2. Cette dernière est initialement au repos à une hauteur h =0 m. Le chronogramme qui suit représente 1'évolution de l'accélération. À l'instant t3, la charge est de nouveau immobile. 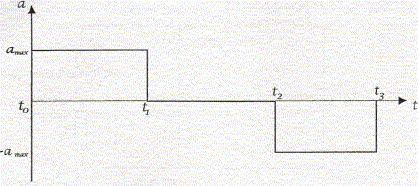 Au temps tl = 3,5 s, la charge a atteint une hauteur h =6 m.
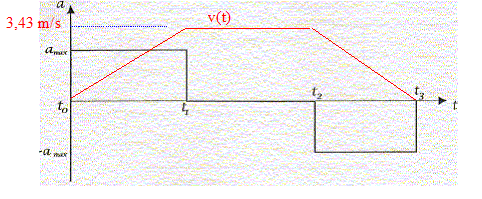
corrigé accélération amax prise par la charge : h=½amaxt12 soit amax = 2h / t12 = 12 / 3,5² = 0,98 m/s² valeur de la tension Tl du câble pendant cette phase de l'ascension : La charge est soumise à son poids ( vertical, vers le bas, valeur mg ) et à la tension T1 du câble, verticale vers le haut. Ecrire la seconde loi de Newton sur un axe vertical ascendant -mg + T1 = mamax soit T1 = m( g+amax ) = 104 *(9,81+0,98) = 1,08 105 N. Dans la seconde phase du mouvement, l'accélération est nulle. T2=mg = 9,81 104 N. vitesses V1 et V2 atteintes au temps t1 et t2 : V1= amax t1 = 0,98*3,5 = 3,43 m/s. entre t1 et t2 le mouvement est rectiligne uniforme : V1 = V2 Calcul du temps t3 : entre t2 et t3 l'accélération est négative (-0,98 m/s²) : la vitesse diminue puis s'annule à la date t3. v3(t) = -amax (t-t2) + v2 = -0,98 (t-6) + 3,43 ; à la date t3 , la vitesse s'annule : d'où : -0,98 (t3-6) + 3,43=0 soit t3-6 = 3,43/0,98 = 3,5 ; t3= 9,5 s.
durée minimale t' de l'ascension pour éviter la rupture du câble : Tmax= 4 l05 N ; P= M'g = 1,5 104*9,81 =1,47 l05 N la seconde loi de Newton s'écrit sur un axe vertical ascendant : Tmax-P= M'a d'où a = (Tmax-P)/M' =2,53 105 / 1,5 104 = 16,867 m/s² h' = ½a t'² soit t'² = 2h'/a = 20 / 16,867 = 1,186 soit t' = 1,09 s.
|
||
|
Les parties qui suivent peuvent être traitées indépendamment. Le générateur de tension a pour fé.m E = 10 V. La résistance a une valeur R =33 W, la bobine une inductance L = 32,0 mH et une résistance r = 6 W et le condensateur une capacité de 620 nF. Initialement, les deux interrupteurs SI et S2 sont ouverts et le condensateur est déchargé. À t =0 s, on ferme l'interrupteur SI.  Partie A : charge du condensateur.
Partie B : circuit rLC. Le condensateur est chargé. La tension aux bornes du condensateur est égale à E. On ouvre alors l'interrupteur SI. À un instant t que l'on choisira comme nouvelle origine du temps, on ferme S2.
corrigé équation différentielle à laquelle obéit la tension aux bornes du condensateur : additivité des tensions : E = uc+Ri de plus i = dq/dt et q=Cuc d'où i = Cd uc /dt E = uc+RCduc /dt ; d uc /dt + uc/(RC) = E/(RC) ; on pose t= RC ; d uc /dt + uc/t= E/t (1) résolution : solution générale de l'équation sans second membre : uc(t) = A exp(-t/t) solution particulière de (1) ( condensateur complétement chargé ) uc=E solution générale de (1) : uc(t) =A exp(-t/t) +E On détermine A par les conditions initiales ( condensateur non chargé, uc(0)=0): 0=A+E soit A=-E : uc(t) = E(1- exp(-t/t)). valeur de la constante de temps : t= RC = 33*620 10-9 = 2,05 10-5 s. cette constante de temps permet d'estimer la durée de la charge du condensateur : le condensateur est pratiquement chargé à t =5t. expression de l'intensité i(t) = C d uc /dt = CE/(RC) exp(-t/t) = E/Rexp(-t/t). le condensateur est pratiquement chargé à t =5t. en effet e(-5) = 6,7 10-3 et 1-e(-5) =0,993 ; à t = 5t, la charge du condensateur atteint 99,3 % de sa valeur maximale. charge emmagasinée q et l'énergie Ec du condensateur chargé : q= CE = 620 10-9*10 = 6,2 10-6C Ec = ½CE² = 310 10-9*100= 3,1 10-5 J. L'énergie Ec du condensateur chargée est en partie transférée dans la bobine inductive : une petite partie est dissipée sous forme de chaleur dans la résistance r. Il y a échange d'énergie entre bobine et condensateur. [L/R]= T ; L/R s'exprime en seconde ; [R²/L²] = T-2 ; R²/L² s'exprime en s-2. On ne peut soustraire que des grandeurs de même dimension : donc 1/(LC) s'exprime en s-2. en conséquence le dénominateur s'exprime en s-1. de plus T , période, s'exprime en seconde : donc k est sans dimension. (r/L)² =( 6/0,032)² =3,5 104 s-2. 1/(LC) = 1/(0,032 * 6,2 10-7)=5 107 s-2, valeur très supérieure à (r/L)² le terme (r/L)² est négligeable devant 1/(LC) d'où T = k (LC)½. la tension aux bornes du condensateur peut changer de signe au cours de la décharge : durant le premier quart de période, le condensateur se décharge à travers la bobine ; celle-ci stocke de l'énergie durant le second quart de période, la bobine restitue de l'énergie au condensateur ; ce dernier se charge en sens contraire de la charge initiale et la tension à ces bornes est de signe contraire à la tension initiale.
|
||
|
|
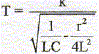 Sachant que L/R et RC sont des durées, donner la
dimension de k.
Sachant que L/R et RC sont des durées, donner la
dimension de k.