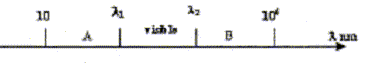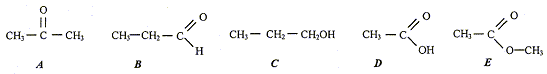Aurélie 05/06

d'après concours manipulateur électroradiologie médicale Lyon 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


Etude du champ magnétique au centre d'un solénoïde

Pour différentes intensités I du courant dans trois solénoïdes de même longueur L, les mesures du champ magnétique B ( mT) au centre de ces derniers ont permis de tracer les graphes suivants :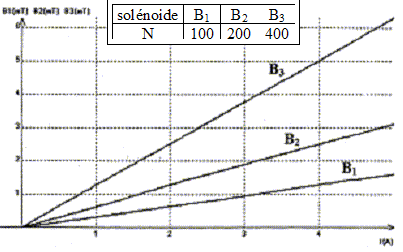

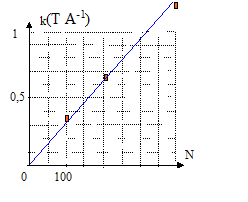
  1. Pour chaque solénoïde montrer que B= k I et déterminer la valeur de k.
  2. Tracer la coube représentative de k en fonction de N, nombre de spires du solénoïde. Conclure.
  3. On effectue la même série de mesures en doublant la longueur L de chaque solénoïde. On constate que la valeur de B est divisée par deux. Comment varie B en fonction de la longueur L ?
  4. Parmi les relations suivantes quelle est celle qui conviendrait au calcul de B ? Justifier.
    B= k'NI ; B= k'IL/N ; B= k'NI/L ; B= k'LN/I, k' est une constante.
corrigé
Les trois graphes sont des droites passant par l'origine : le champ et l'intensité du courant sont proportionnelles soit B= k I avec k, constante de proportionnalité.

k1 = 10-3 / 3 = 3,33 10-4 T A-1 ; k2 = 2,5 10-3 / 4 = 6,25 10-4 T A-1 ; k3 = 5 10-3 / 4 = 12,5 10-4 T A-1 ;

coube représentative de k en fonction de N, nombre de spires du solénoïde ( k a été multiplié par 103 sur le graphe)

k et N sont proportionnels ; de plus B= kI d'où B= k'NI ( k' = constante)

le champ B et la longueur du solénoïde L sont inversement proportionnels : quand l'un double, l'autre est divisé par 2.

B= k'NI / L convient car :
- B et I sont proportionnels ; B et N sont proportionnels ; B et L sont inversement proportionels.


Ondes électromagnétiques
  1. Le spectre des ondes électromagnétiques est partagé en plusieurs parties.
    - Pour chacun des domaines A et B donner son nom.
    - Donner les valeurs des longueurs d'ondes l1 et l 2.
  2. On considère une onde de fréquence n= 640 1012 Hz. A quelle vitesse se déplace-t-elle dans le vide ?
    - A quel domaine appartient cette onde ? Justifier.
  3. On envisage le passage de cette onde dans un milieu d'indice n= 1,5. Déterminer sa vitesse dans ce milieu.
    - La fréquence de l'onde est-elle différente dans le milieu d'indice n ? Si oui préciser si elle est plus petite ou plus grande ? Même question pour la longueur d'onde.
  4. Proposer une source de lumière monochromatique.
corrigé
domaine A : infrarouge (IR) ; domaine B : ultraviolet (UV)

longueurs d'ondes l1 : 800 nm et l 2 = 400 nm

une onde de fréquence n= 640 1012 Hz se déplace dans le vide à la célérité de la lumière c = 3 108 m/s.

domaine auquel appartient cette onde : l = c/n =3 108 /640 1012 =4,7 10-7 m = 470 nm, valeur comprise entrel1 et l 2, donc domaine "visible".

vitesse de l'onde dans le milieu d'indice n=1,5 : c/n=3 108/1,5 =2 108 m/s.

La fréquence de l'onde caractérise l'onde : elle reste constante quel que soit le milieu traversé par l'onde.

l = c/n : n étant constant, la célérité c dépend du milieu , donc la longueur d'onde dépend du milieu traversé ; dans ce milieu d'indice n la longueur d'onde diminue et vaut l 0/n, l 0 longueur d'onde dans le vide.

La lumière "laser" est une source de lumière monochromatique.


radioactivité

Données : césium 55Cs ; xénon 54Xe ; baryum 56 Ba ; iode 53I.

En 1986, lors de la catastrphe de Tchernobyl, l'explosion d'un réacteur nucléaire a provoqué la libération, dans l'atmosphère, de césium 134 et 137.

  1. Quel est le point commun entre le césium 134 et le césium 137. Comment les qualifie-t-on ?
  2. Donner la composition d'un noyau de césium 137.
  3. Le césium 137 est un noyau radioactif b-. Ecrire l'équation de la désintégration de ce noyau en précisant la nature des produits formés.
  4. Cette désintégration peut donner un rayonnement g. Quel est la nature de ce rayonnement ?
  5. Les temps de demi-vie du césium 137 et du césium 134 sont respectivement 30 ans et 2 ans.
    - Donner la définition du temps de demi-vie.
    - En considérant une activité initiale A0 = 3,0 104 Bq pour chaque césium, démontrer que l'activité au bout d'une demi-vie est ½A0.
corrigé
point commun entre le césium 134 et le césium 137 : isotopes, ils ont le même nombre de protons, mais des nombres de neutrons différents.

composition d'un noyau de césium 137 : 55 protons ; 137-55 = 82 neutrons.

équation de la désintégration de ce noyau : 13755Cs = AZX+0-1e ( électron)

conservation de la charge : 55=Z-1 soit Z= 56 ( élément baryum 56Ba)

conservation du nombre de nucléons : 137 =A+0

Le rayonnement g appartient aux ondes électromagnétiques.

définition du temps de demi-vie t½ : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.

Or A= l N avec l constante radioactive et N nombre de noyaux présents à la date t.

à t=0 : A0 =l N0 ; à t½ : Nt½=½N0 d'où At½ = l½N0 = ½A0.

dilutions homéopathiques

Lors de la fabrication de spécialités homéopathiques on effectue des dilutions successives à partir d'une solution de base ( la teinture mère TM). La première dilution ou première centésimale Hahnemanienne ( 1 CH) consiste à ajouter 99 gouttes de sovlant à une goutte de teinture mère et à agiter vigoureusement. La seconde dilution consiste à ajouter 99 gouttes de sovlant à une goutte de solution 1CH et à agiter vigoureusement, on obtient la solution 2CH et ainsi de suite.

  1. Quel est le facteur de dilution quand on passe de la teinture mère à la solution 1 CH. Justifier.
  2. Même question quand on passe de la teinture mère à 2 CH ? à 3CH ?
  3. Si la concentration en principe actif de la teinture mère vaut c= 1,0 mol/L, que valent les concentrations c1, c2, c3 en principe actif des solutions 1CH, 2CH et 3CH ?
  4. Quelle est la concentration c12 en principe actif de la solution 12 CH ?
    - Combien de molécules de principe actif contient 1 L de solution 12 CH ? NA= 6 1023 mol-1.
corrigé
facteur de dilution quand on passe de la teinture mère à la solution 1 CH.

F1= volume solution fille 1CH / volume solution mère = nombre total de gouttes / nombre de goutte issue de la solution mère = 102.

F2 =F1*F1 = 104 ; F3 = 106

c1 = c/F1 = 1/102 = 1,0 10-2 mol/L ; c2 = 1,0 10-4 mol/L ; c3 = 1,0 10-6 mol/L ; c12 = 1,0 10-24 mol/L

nombre de molécules de principe actif dans 1 L de solution 12 CH : c12 NA= 1,0 10-24 * 6 1023 = 0,6.

composés organiques oxygénés
  1. Entourer et nommer les fonctions chimiques présentes dans les molécules A, B, C, D, E.
  2. Certaines de ces molécules sont isomères. Lesquelles ?
  3. Les composées C et D sont des liquides, leur mélange subit une transformation modélisée par la réaction d'équation :

    Quel est le nom de cette réaction ?
  4. On verse 150 mL de composé C dans 120 mL de composé D, lorsque la transformation est terminée le mélange contient entre autre 4/3 moles de composé F.
    - Déterminer en moles la composition initiale du mélange.
    - La transformation est-elle totale ? Justifier.
    - Déterminer en mole la composition du mélange final.
    C : M(C)= 60 g/mol ; masse volumique 0,80 g/mL ; D : M(D) = 60 g/mol ; masse volumique 1,0 g/mL.
corrigé

isomères : même formule brute, mais des formules développées différentes. A et B ( C3H6O)

Les composées C et D sont des liquides, leur mélange subit une transformation : estérification.

composition initiale du mélange : mC=150*0,8 = 120 g ; n(C) = mC/M(C) = 120/60 = 2 mol

mD=120*1 = 120 g ; n(D) = mD/M(D) = 120/60 = 2 mol

Si la transformation était totale, on devrait obtenit 2 mol de F. Or on obtient seulement 4/3 mol de F, donc la transformation est limitée.

composition du mélange final : C et D : 2-4/3 = 2/ 3 mol ; F : 4/3 mol ; eau : 4/3 mol

Oxydo-réduction

Lorsqu'on verse de l'acide chlorhydrique dans une solution de thiosulfate de sodium on observe la lente apparition d'un précipité blanc jaunatre de soufre. Cette transformation est modélisée par la réaction d'équation : S2O32- aq + 2H+ = S (s) + SO2(g) + H2O (l)

  1. Montrer que l'on peut interprèter cette réaction comme une oxydo-réduction faisant intervenir les couples : S2O32- aq/ S(s) et SO2(g)/S2O32- aq
  2. Quel est l'oxydant ? Quel est le réducteur ?
  3. Justifier l'appellation " dismutation" des ions thiosulfate en milieu acide, donnée à cette équation.
corrigé
S2O32- aq +6H++ 4e- = 2 S(s) + 3H2O réduction ; S2O32- joue le rôle d'oxydant du couple S2O32- aq/ S(s)

S2O32- aq + H2O = 2SO2(g) + 4e- +2H+ oxydation ; S2O32- joue le rôle de réducteur du couple SO2(g)/S2O32- aq

ajouter ces deux demi-équations : 2S2O32- aq +4H+ = 2 S(s) + 2H2O+ 2SO2(g)

les ions thiosulfates jouent un double rôle, oxydant et réducteur d'où le nom "dismutation" donné à cette équation.

retour -menu