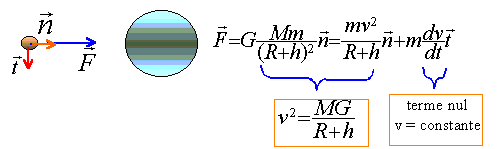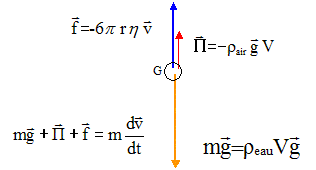|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Un satellite de masse m est en orbite dans le vide sidéral autour de la Terre ( masse MT et rayon RT)
corrigé les autres forces négligées : forces attractives de gravitation exercées par la Lune, le Soleil et les autres planètes. intensité de la force de gravitation terrestre agisant sur ce satellite : F= G MT m / (RT+h)² On étudie le mouvement du satellite dans le référentiel géocentrique, considéré comme galiléen. le satelitte est soumis à la seule force de gravitation, dirigée vers le centre de la Terre. le théorème du centre d’inertie, dans la base de Frenet s'écrit : h est l'altitude et RT le rayon terrestre
La valeur de la vitesse étant constante, le mouvement est uniforme. En négligeant l'action des autres planètes, de la Lune et du Soleil, le satellite n'est soumis qu'à la focre centipète de gravitation de la Terre ; de plus la force de gravitation est perpendiculaire au vecteur vitesse : la trajectoire est plane et circulaire. v²= MTG/(RT+h )= 6 1024 * 6,7 10-11 / ((6400+300) 103)= 6 1013 * 6,7 / (6,7 106) = 6 107 = 60 106 ; v = 7,75 103 m/s = 7,75 km/s.
|
|
|
|
||
|
Les microgouttelettes d'eau ( suposées sphériques de rayon r) d'un nuage tombe dans l'atmosphère avec une vitesse v. ( les vecteurs sont écrits en gras et en bleu).
Données : r = 1mm ; reau= 1000 kg/m3 ; rair= 1,3 kg/m3 ; h = 20 10-6 SI ; g = 10 m/s² ; 1/9 = 0,11 corrigé la goutte est soumise à son poids, (vertical, vers le bas, valeur mg), à la poussée d'Archimède, ( verticale, vers le haut, valeur égale au poids du volume d'air déplacé) et aux forces de frottement dues à l'air.
La masse volumique de l'air étant environ 700 fois plus petite que la masse volumique de l'eau, la poussée d'Archimède est négligeable devant le poids. équation différentielle de la gouttelette : écrire la seconde loi de Newton sur un axe vertical, orienté vers le bas. mg - 6p r h v = mdv/dt avec m = reau 4/3 p r3. diviser par m : dv/dt + 4,5 r-2 h/ reau v = g expression de la vitesse limite de chute : la vitesse limite vlim étant atteinte le mouvement est uniforme ( dvlim/dt=0 ) d'où 4,5 r-2 h/ reau v lim = g soit vlim= g reaur² /(4,5h) vlim= 10 *103* 10-12/(4,5*20 10-6)=10-8/(9 10-5) = 10-3 / 9 = 0,11 10-3 = 1,1 10-4 m/s. Comparaison de cette vitesse limite à celle d'une goutte de pluie dont le rayon r'=200 r. r'² = 4 104 r² et la vitesse limite est proportionnelle à r² : v'lim = 4 104 vlim = 4,4 m/s.
|
||
|
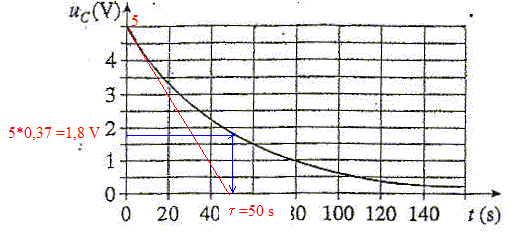
Un condensateur de capacité C, initialement chargé sous une tension U= 5 V est déchargé à travers un conducteur ohmique de résistance R= 10 kW. On visualise la tenion uc aux bornes du condensateur au cours de la décharge. 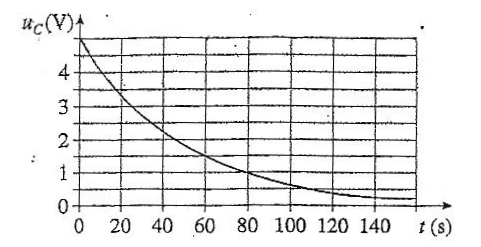
corrigé équation différentielle du circuit de décharge 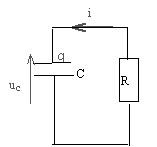
uc + Ri = 0 avec q = Cuc et i = dq/dt = C duc /dt d'où : uc + RCduc /dt =0 (1) uc (t) = U exp( -t/(RC)) ; duc /dt = U/(-RC) exp( -t/(RC)) repport dans (1) : U exp( -t/(RC)) +RC U/(-RC) exp( -t/(RC)) =0 vérifié quel que soit t. donc uc(t)= U exp( -t/(RC)) est solution de cette équation. constante de temps du circuit : C= t/R = 50 / 104 = 5 10-3 F.
|
||
|
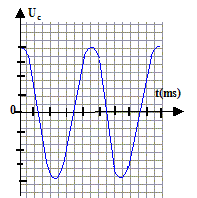
Un condensateur de capacité C= 10 mF, initialement chargé sous une tension U=6 V est placé dans le circuit suivant : 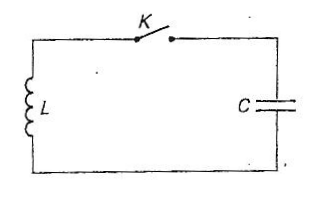
corrigé 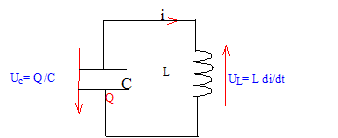
uc+uL=0 avec Cuc= Q ; uL= Ldi/dt et i = dQ/dt = Cduc/dt soit di/dt = Cd²uc/dt² équation différentielle à laquelle obéit la tension uc : uc+LCd²uc/dt² =0 ou d²uc/dt² +w² uc=0 avec w²= 1/(LC) w²= 1/(0,1*10-5) = 106 ; w = 103rad/s. valeurs de a et b : uc(0) =U= 6 = a cos(b) d'où a= U= 6V et cos b=1 soit b=0 période T des oscillations : T = 2p/w= 6,28 10-3 s. allure de la courbe uc(t)
sur deux périodes
|
||
Données : exp[(-ln2)*6/15] = 0,75 ; exp[(-ln2)*15/6] = 0,18 ; corrigé réaction de formation du sodium 24 : 2311Na + 01n = 2411Na conservation de la charge : 11+0 = 11 conservation du nombre de nucléons : 23+1 = 24 équation de désintégration du sodium 24 : 2411Na = 2412Mg + -10e loi de décroissance radioactive : A= A0 exp(-lt) A : activité à la date t ( Bq) ; A0 : activité à la date t=0 ( Bq) ; l constante radioactive ( s-1) ; t : temps en seconde. demi-vie t½ d'un élément radioactif : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés ( l'activité a diminué de moitié) ½A0= A0 exp(-lt½) : 0,5 = exp(-lt½) ; ln 2 = lt½ nombre de mole de sodium 24 introduit dans le sang : n= cv = 10-3 * 10-2 = 10-5 mol. au bout de 6 h il en reste : n= 10-5 exp(-6l) avec l en heure-1. ln 2 = lt½ donne l = ln2 /15 n= 10-5 exp(-6 ln2 /15) = 10-5*0,75 = 7,5 10-6 mol volume sanguin : 1,5 10-8 mol dans 10 mL ou 0,01 L 7,5 10-6 mol dans V litres de sang ; V= 7,5 10-6*0,01 / 1,5 10-8 = 5 L.
|
||
|
Soit un cube de glace d'arête h placé à la surface de l'eau contenue dans une cuve. L'altitude de la surface de l'eau est supposée constante, le volume de la cuve étant très grand devant celui du glaçon. Soit z(t) l'ordonnée de la surface inférieure du glaçon. 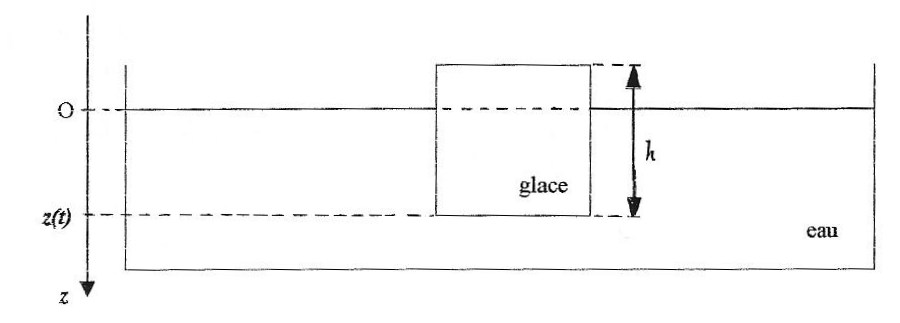
corrigé relation entre l'ordonnée à l'équilibre zéq et l'arrête h lorsque le glaçon est immobile : le glaçon est soumis à deux forces opposées, son poids et la poussée d'Archimède : reau zéqh2 g = rglace h3 g soit reau zéq = rglace h zéq = 0,9 h équation différentielle du mouvement du glaçon : le glaçon est soumis à son poids, vertical, vers le bas, valeur rglace h3 g et à la poussée d'Archimède reau z h2 g. écrire la seconde loi de Newton sur l'axe Oz : rglace h3 g- reau z h2 g = rglace h3 d²z/dt² diviser par rglace h3 : g- reau /rglace g z h2 /h3 = d²z/dt² ; d²z/dt² + reau /(rglace h) g z = g ; w02 =r eaug/(rglace h). Expressions de A, B et C en fonction de zéq et z0 : à t=0 z= z0 ; z0 = A + C vitesse z'= -Aw0sin (w0t) + Bw0cos (w0t) la vitesse est nulle à t=0 d'où : 0= B w0 ; w0 n'étant pas nul alors B=0. z" = -Aw20cos (w0t)- Bw20sin (w0t) = -Aw20cos (w0t) repporter z" et z dans l'équation différentielle : -Aw20cos (w0t) +w20(Acos ( w0t) +C)=g ; d'où C= g/w20 = rglace h/r eau=0,9 h = zéq or z0 = A + C d'où : A= z0 -zéq
|
||
|
|