|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Soit un cube de glace d'arête h placé à la surface de l'eau contenue dans une cuve. L'altitude de la surface de l'eau est supposée constante, le volume de la cuve étant très grand devant celui du glaçon. Soit z(t) l'ordonnée de la surface inférieure du glaçon. 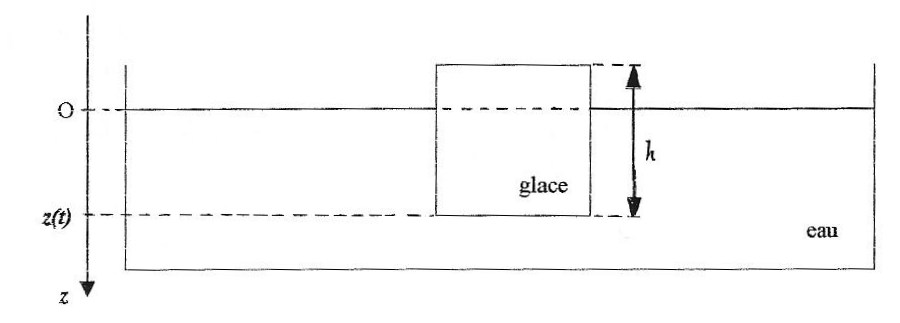
le glaçon est soumis à deux forces opposées, son poids et la poussée d'Archimède : reau zéqh2 g = rglace h3 g soit reau zéq = rglace h zéq = 0,9 h équation différentielle du mouvement du glaçon : le glaçon est soumis à son poids, vertical, vers le bas, valeur rglace h3 g et à la poussée d'Archimède reau z h2 g. écrire la seconde loi de Newton sur l'axe Oz : rglace h3 g- reau z h2 g = rglace h3 d²z/dt² diviser par rglace h3 : g- reau /rglace g z h2 /h3 = d²z/dt² ; d²z/dt² + reau /(rglace h) g z = g ; w02 =r eaug/(rglace h). Expressions de A, B et C en fonction de zéq et z0 : à t=0 z= z0 ; z0 = A + C vitesse z'= -Aw0sin (w0t) + Bw0cos (w0t) la vitesse est nulle à t=0 d'où : 0= B w0 ; w0 n'étant pas nul alors B=0. z" = -Aw20cos (w0t)- Bw20sin (w0t) = -Aw20cos (w0t) repporter z" et z dans l'équation différentielle : -Aw20cos (w0t) +w20(Acos ( w0t) +C)=g ; d'où C= g/w20 = rglace h/r eau=0,9 h = zéq or z0 = A + C d'où : A= z0 -zéq
|
|
|
|