Aurélie 05/06

Dosage du peroxyde d'hydrogène dans une solution commerciale d'eau oxygénée : d'après concours technicien chimiste Lille 2003

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


problème 6

A- Dosage du peroxyde d'hydrogène dans une solution commerciale d'eau oxygénée :

10 mL d'une solution commerciale S1 sont dilués par de l'eau dans une fiole jaugée de 200 mL pour fournir une solution S2.

10 mL de cette solution S2 sont mis dans un erlenmeyer contenant une solution d'iodure de potassium en excès et 5 mL d'acide sulfurique.

  1. Ecrire les deux demi-équations ainsi que l'équation bilan de l'oxydation des ions iodures par l'eau oxygénée, en milieu acide.
    Le contenu de l'erlenmeyer est dosé par une solution de thiosulfate de sodium de molarité 0,12 mol/L.
  2. Ecrire les deux demi-équations ainsi que l'équation bilan du dosage du diiode par le thiosulfate de sodium.
    La décoloration du diiode intervient pour un volume moyen de 13,85 mL de thiosulfate de sodium versé.
  3. Calculer la molarité en eau oxygénée des solutions S2 puis S1.
  4. Sachant que le titre " en volume" d'une eau oxygénée est le nombre de litres de dioxygène qui serait libérée par une solution d'eau oxygénée selon la réaction (1) : H2O2--> H2O+½O2. Déterminer le titre "en volume" de la solution commerciale.

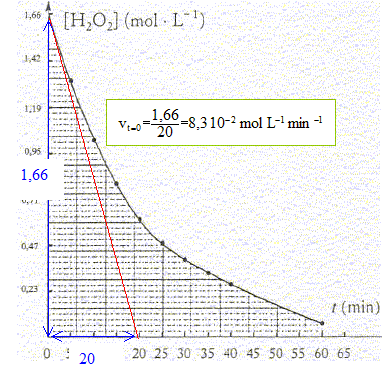
B- On se propose de suivre la disparition du peroxyde d'hydrogène au cours de sa décomposition selon la réaction (1) précédente. Cette expérience est réalisée à température ambiante. Le graphe représente l'évolution de la concentration en peroxyde d'hydrogène en fonction du temps.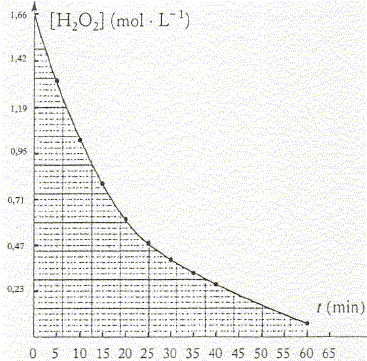

  1. Définir la vitesse moyene de disparition du composé. La calculer dans l'intervalle de temps [15 ; 30 min]
  2. Définir la vitesse instantanée de disparition de H2O2. La calculer à t=0.
    - Comment évolue cette vitesse au cours du temps ? Expliquer.

Données : Vm=22,4 L/mol ; I2/I- (E°=0,54 V) ; S4O62- /2S2O32- (E°=0,07 V) ; H2O2/H2O (E°=1,77 V).

corrigé
équation bilan de l'oxydation des ions iodures par l'eau oxygénée, en milieu acide :

H2O2+2H++2e- =2H2O réduction ; 2I- = I2+2e- oxydation

H2O2+2H++2I- = I2+2H2O (1)

équation bilan du dosage du diiode par le thiosulfate :

2S2O32- = S4O62-+2e- oxydation ; I2+2e- =2I- réduction
2S2O32- + I2 = S4O62- + 2I- d'où n(I2) =½n(S2O32-)

n(S2O32-) = 13,85 10-3*0,12 = 1,66 10-3 mol ; n(I2) = 8,3 10-4 mol

d'après (1) : n(I2) = n(H2O2)= 8,3 10-4 mol dans 10 mL de S2.

molarité en eau oxygénée des solutions S2 puis S1: [H2O2]S2 = 8,3 10-4/10-2 = 8,3 10-2 mol/L

facteur de dilution F= 200/10 = 20 d'où [H2O2]S1 =20 [H2O2]S2 = 20* 8,3 10-2= 1,66 mol/L

titre "en volume" de la solution commerciale :

d'après H2O2--> H2O+½O2, n(O2) = ½n(H2O2) = 1,66/2 = 0,83 mol dans 1L

0,83*volume molaire des gaz = 0,83*22,4 = 18,6 volumes.

vitesse moyene de disparition du composé dans l'intervalle de temps [15 ; 30 min] :

vmoy = | [H2O2]30-[H2O2]15| / (30-15) = |0,40-0,80|/15= 0,4/15 = 2,7 10-2 mol L-1 min-1.

vitesse instantanée de disparition de H2O2 : v=- 1/V dx/dt avec V: volume de la solution (L) et x avancement de la réaction ; v= -d[H2O2]/dt

cette vitesse diminue au cours du temps car la concentration ( facteur cinétique) d'eau oxygénée diminue au cours du temps.

retour -menu