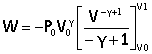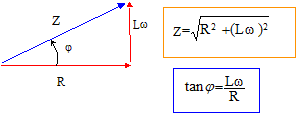|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||
| .
. |
|||||
|
|||||
|
|
A. Dans une carabine à air comprimé, une masse d'air (assimilée à un gaz parfait) telle que g=1,4, ocupe un volume V= 5 cm3 sous la pression P0 =106 Pa, à la température de 15°C. Cette masse d'air se détend adiabatiquement dans le canon de longueur L=1 m et de section s= 0,25 cm², en propulsant le projectile de masse m= 1g, dans l'atmosphère.
B. En réalité v0 = 90 m/s. Un enfant envisage de chasser un moineau avec cette carabine. On se propose d'étudier la trajectoire du projectile. Un moineau M est posé sur la cime d'un arbre à une hauteur h= 6,30 m. Lorsque l'enfant épaule l'extrémité C du canon se situe à H= 1,30 m du sol. L'arbre est distant de L= 15 m de l'extrémité du canon. On néglige la résistance de l'air.
corrigé pression P1 de la masse d'air à la fin de la détente : P0Vg= P1V1g soit P1 = P0(V/V1)g avec V1= Ls = 100*0,25 = 25 cm3 ; P1 =106 (5/25)1,4 = 1,05 105 Pa. température de la masse d'air à la fin de la détente : P1V1= nRT1 avec n= P0V/(RT0) T1 = P1/P0 V1/V T0 = 0,105 * 5*(273+15) = 151,2 K. travail W fourni par la masse d'air au cours de la détente : dW= - PdV et P = P0V0g /V g. dW=-P0V0g dV/V g. On intègre : W = 106 (5 10-6)1,4 / 0,4 [(25 10-6])-0,4-(5 10-6)-0,4] = -5,93 J. Vitesse à la sortie du canon : la balle emporte ce travail sous forme d'énergie cinétique ½mv² d'où v² = 2W/m = 2*5,93 / 10-3 = 11863 ; v = 109 m/s. 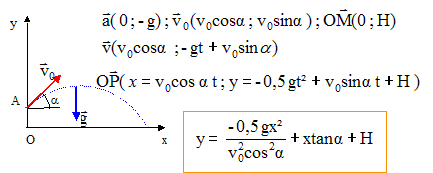
Calcul de y pour x=L=15 m ; v0 = 90 m/s ; tan a = (h-H) / L = 5/15 = 0,333 soit a = 18,43° ; cos a =0,9486 ; H= 1,30 m y = -0,5*9,81*152 / (90*0,9486)2 +15*0,3333 +1,30 = 6,148 m soit MI= 0,152 m. angle b : dans l'expression précédente , l'inconnue est cos b avec y= 6,30 m y-H = 5 m ; -0,5gL²/v0² = -0,5*9,81*15²/90² =-0,136 ; 1+ tan² b = 1/cos²b d'où : 5 = -0,1362 (1+ tan² b)+ 15 tan b ; on pose X= tan b -5 -0,136 (1+ X²)+ 15X=0 soit -0,136X² + 15X-5,136 =0 X=0,343 soit b= tan-1 0,343 = 18,93°. La différence entre a et b est voisine de 0,5°.
|
||||
|
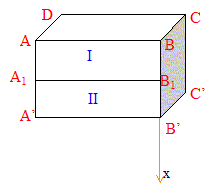
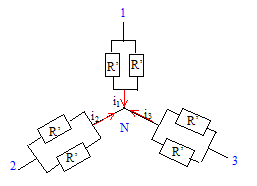
On considère un grand bassin rectangulaire rempli entièrement d'eau. AD=A'D'=BC=B'C'= l =4 m ; AB=A'B'=DC=D'C'=L=8 m ; AA'=BB'=CC'=DD'=H=9 m La paroi verticale ABB'A' est formée de deux panneaux plans superposés ( I et II). On note AA1=h1 et A1A'=h2.
corrigé On note p0 la pression de l'air ambiant au dessus du liquide. pression dans le liquide à une altitude x : la surface du liquide est l'altitude x=0 ; l'axe vertical est orienté vers le bas. pression exercée par l'air + pression due à la hauteur de la colonne liquide : p = p0+ r g x force élémentaire pressante due à l'eau sur une surface dS =Ldx de largeur L de hauteur dx située à l'altitude x : dF= p dS = (p0+ r g x) Ldx dirigée vers l'extérieur du liquide panneau (I), intégrer entre 0 et h1 : L[p0x+ ½r g x2] 0h1 =Lh1[p0+ ½r g h1 ]. force pressante exercée par l'air sur cc panneau (I) : p0Lh1, dirigée vers l'intérieur du liquide soit au total : F1=½r g L h21, perpendiculaire au panneau et dirigé vers l'extérieur du liquide. panneau (II), intégrer entre h1 et H : L[p0x+ ½r g x2] h1H =L[p0h2 +½r g ( H2-h21 )]. force pressante exercée par l'air sur ce panneau (II) : p0Lh2, dirigée vers l'intérieur du liquide soit au total : F2=½r g L ( H2-h21 ), perpendiculaire au panneau et dirigé vers l'extérieur du liquide. F1=F2 donne : h21=H2-h21 soit 2h21=H2 ou : h1 =2-½H. h1
=0,707 H = 0,707*9 =6,4
m ; h2
= 9-6,4 = 2,6 m.
La vitesse est quasiment nulle en A car la surface libre est très supérieure à la section du trou ; pA=p0=105 Pa ( pression atmosphérique) A la sortie l'eau est en contact avec l'air pT= p0=105 Pa ½rvA²+pA+rg xA=½rvT²+pT+rg xB s'écrit : g xA=½vT²+g xB ; vT²= 2 g(xB - xA) = 2gh ( h : hauteur d'eau au dessus du trou) vT= [2gh]½ ; si h= h1 alors vT= [2*9,8*6,4]½ = 11,2 m/s. débit volumique correspondant ( m3/s ) = section (m²) fois vitesse (m/s) = 5 10-4*11,2 = 5,6 m3/s = 5,6 L/s.
|
|||||
|
Un dispositif d'éclairage urbain comprend 6 projecteurs
d'une puissance de 1150 W chacun sous une tension nominale de 230 V.
A. Alimentation en triphasé :230 - 400 V - 50 Hz
corrigé 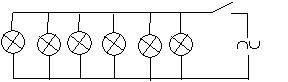
intensité du courant qui traverse l'interrupteur si on considère que les projecteurs sont uniquement résistifs : I= P/U = 1150/230 = 5 A dans chaque branche dérivée Les courants dérivés
s'ajoutent : 6*5 = 30 A traversent l'interrupteur.
cos j=
0,8 d'où tan j = 0,75 Lw=
R tan j avec R= U/I =
230/5 = 46 W soit Lw=
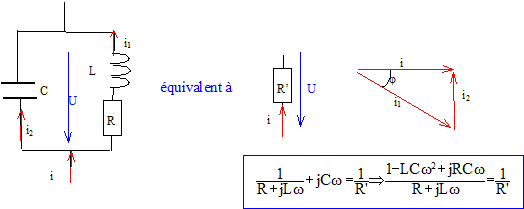
46*0,75 = 34,5 W ; L= 34,5 / 314 = 0,11 H Z=[462+34,52]½=57,5 W identifier parties réelle et imaginaire : R'( 1-LCw²)= R et L=R'RC d'où R'= L/(RC) et C= L/( R²+(Lw)²) = 0,11 / 57,52
= 3,32 10-5 F = 33,2
mF. R' = 0,11 / (46*3,32 10-5)
= 72 W. L'intensité du courant dans l'ensemble projecteur- condensateur vaut : 230 / 72 = 3,2 A soit 6*3,2 = 19,2 A. Intensité du courant dans le condensateur : I2 = I tanj = 3,2 *0,75 = 2,4 A. Si on n'avait pas mis de condensateurs, l'intensité du courant dans l'interrupteur serait : impédance de la bobine : Z=[46²+34,5²)½=57,5 W ; I= U/Z = 230 / 57,5 = 4 A dans chaque projecteur ; soit 4*6 = 24 A dans l'interrupteur. déphasage de ce courant par rapport à la tension : tan j = 34,5/ 46 = 0,75 ; j = 0,64 rad courant en retard sur la tension de -0,64 rad.
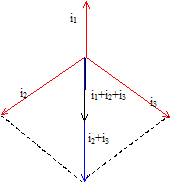
intensité du courant dans les fils de ligne et dans le neutre : Deux ensembles projecteur-condensateur en dérivation sont équivalents à un dipôle d'impédance ½R' = 36 W d'où l'intensité en ligne : I=230/36 = 6,39 A. Dans le fil neutre, l'intensité est nulle, le système étant équilibré. L'un des projecteur grille dans la phase 1, l'intensité dans les fils de ligne et le neutre vaut : dans la phase 2 et dans la phase 3 : I= 6,39 A dans la phase 1, l'impédance double donc l'intensité est divisée par 2 : I1 =3,2 A Le montage est déséquilibré : dans le neutre l'intensité vaut : 3,2 A.
|
|||||
|
|