Aurélie 16/10/06

 

physique chimie ( d'après concours interne ingénieur territorial 2006) Triphasé ; projectile ; hydrostatique ; énergétique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Electricité : (4 pts)
  1. On branche un chauffe eau électrique sur une installation triphasée( 230 / 400 V ; 50 Hz ) La partie électrique est constituée de trois résistances de 46 W chacune montées en étoile.
    - Calculer la valeur de l'intensité efficace dans chaque fil de ligne.
    - Donner la valeur de la puissance active consommée.
  2. La résistance placée entre la phase 3 et le neutre grille. Calculer alors les intensités efficaces dans les fils de ligne et le neutre. Donner la nouvelle valeur de la puissance.
  3. On remplace le chauffe eau par les deux appareils suivants :
    - Une résistance de valeur R1 = 11,5     W entre la phase 1 et le neutre.
    - Une bobine d'impédance 11,5     W, de résistance R2 = 5,75 W et d'inductance L entre la phase 2 et le neutre.

    Calculer la valeur de l'intensité dans le neutre et conclure.

 corrigé
Dans un montage étoile, l'intensité dans un fil de ligne et dans un résistor est la même. La tension aux bornes du résistor est la tension simple V= 230 V.

Par suite I= V/R = 230 / 46 = 5 A.
valeur de la puissance active consommée : P=3½UI cos j.

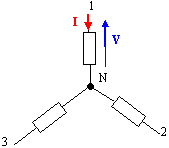
La rension aux bornes d'un résistor et l'intensité qui le traverse sont en phase : cos j = 1.

U : tension composée 400 V ; I : intensité en ligne.

P= 1,732*400*5 = 3,5 kW.

La résistance placée entre la phase 3 et le neutre grille.
Les intensités efficaces dans les fils de ligne valent : i1=i2 = 5 A et i3=0

L'intensité est traversé par la somme des intensités soit 5 A.

Nouvelle valeur de la puissance. P=2/3*1,732*400*5 = 2,3 kW.

On remplace le chauffe eau par les deux appareils suivants :
- Une résistance de valeur R1 = 11,5 W entre la phase 1 et le neutre.

La rension aux bornes du résistor R1 et l'intensité i1 qui le traverse sont en phase : i1=V/R1= 230/11,5 = 20 A.
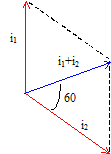
- Une bobine d'impédance 11,5 W, de résistance R2 = 5,75 W et d'inductance L entre la phase 2 et le neutre.

La tension aux bornes d'une bobine inductive est en avance sur l'intensité i2 : cos j = R2/Z= 5,75/11,5 = 0,5 ; j = 60°

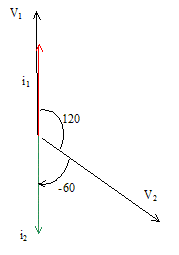
valeur de l'intensité : i2 = V/Z= 230/11,5 = 20 A

i1 et i2 sont en opposition de phase : l'intensité dans le neutre est nulle.
 

 

Mécanique : (3 pts)

Les serveurs d'un canon observent le lancement à partir du territoire nnemi d'un ballon radiocommandé doté d'un équipement espion. Quand ils aperçoivent le ballon pour la première fois, celui-ci se trouve à une altitude de 800 m et monte verticalement à la vitesse constante de 5 m/s. Les obus tirés par le canon possèdent une vitesse initiale de 400 m/s avec un angle de tir q ( cos q = 0,8 ; sin q = 0,6). Les serveurs du canon attendent et font feu au bon moment pour détruire le ballon. On néglige la résistance de l'air et on prend g= 10 m/s².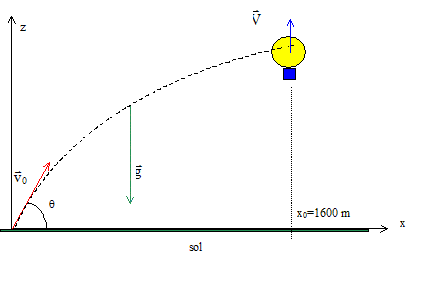

  1. Quelle est la durée de vol de l'obus avant qu'il n'atteigne la cible ?
  2. A quelle altitude a lieu la collision ?
  3. Combien de temps les serveurs attendent-ils avant de faire feu ?
    N.B : les équations horaires seront démontrées.
 corrigé
L'origine des altitudes est le sol.

Mouvement du ballon : rectiligne uniforme

on choisit l'origine des temps à l'instant où le ballon est aperçu ; son altitude est h0 = 800 m

zB= V t1 + h0 = 5t1+800

Mouvement de l'obus : on choisit l'origine des temps à l'instant du tir

dans le repère, les composantes de l'accélération sont : (0 ; -g)

Composantes de la vitesse initiale : v0 cosq ; v0 sinq ;

Le vecteur vitesse est une primitive du vecteur accélération ; les composantes du vecteur vitesse sont : v0 cosq ; -gt + v0 sinq ;

Le vecteur position est une primitive du vecteur vitesse ; les composantes du vecteur position sont :

x= v0 cosq t ; x= 400*0,8 t = 320 t.

z= -½gt² + v0 sinq t ; z = -5t²+ 400*0,6 t = -5t²+240 t.

Durée de vol de l'obus avant qu'il n'atteigne la cible :

la cible est atteinte lorsque x= 1600 m ; 1600 = 320 t soit t = 5s.

Altitude de la collision :

z= -5*25+240*5 = 1075 m.

Les serveurs attendent avant de faire feu :

durée de l'ascension entre 800 et 1075 m : 1075 = 5t1+800 ; t1 = 275/5 = 55 s.

les serveurs attendent : 55-5 = 50 s. 


Hydrostatique : (2 pts)

Le tube en U ci-après est fermé à son extrémité gauche. Il est rempli de deux liquides non miscibles de masses volumiques r1= 1000 kg m-3 et r2= 13600 kg m-3. La branche de gauche renferme un gaz à la pression P0 = 111 600 Pa et la branche de droite est ouverte sur l'atmosphère. Patm = 105 Pa.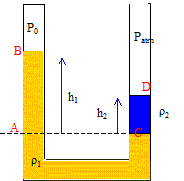
Déterminer l'expression littérale de h1 en fonction de h2 et des autres paramètres ; calculer h1si h2 = 10 cm.

 corrigé
Dans un liquide homogène, la pression est la même en tout point du même plan horizontal : PA=PC.

Expression de la pression au point A ( branche de gauche) : PA=P0+ r1gh1.

 Expression de la pression au point C ( branche de droite) : PC=Patm+ r2gh2.

PA=PC d'où : P0+ r1gh1 =Patm+ r2gh2 ; r1gh1 = Patm- P0+ r2gh2 ; h1 = (Patm- P0)/ (r1g ) +r2 /r1h2 ;

h1 = -11600/(10 000) + 13,6*0,1 =0,2 m.


Energétique: (1 pt)

Sous pression atmosphérique normale, exprimer puis calculer l'énergie nécessaire pour amener m= 10 kg de glace prise à 0°C, à l'état de vapeur à 100 °C.

On donne la chaleur latente de fusion de la glace Lf= 335 000 J/kg, chaleur latente de vaporisation de l'eau Lv= 2 225 000 J/kg et la chaleur massique de l'eau : c= 4185 J kg-1 K-1.

 corrigé
Energie nécessaire pour fondre 10 kg de glace à °C : on obtient 10 kg d'eau à cette température.

La chaleur latente de fusion de la glace est l'énergie qu'il faut fournir pour faire fondre 1 kg de glace à °C

Q1 = m Lf.

 Energie nécessaire pour élever la température de 10 kg d'eau de 0°C à 100°C : l'eau reste liquide

la chaleur massique est l'énergie qu'il faut fournir à 1 kg d'un corps pour élever sa température de 1°C

Q2 = mc Dq avec Dq = 100 °C.

Energie nécessaire pour vaporiser 10 kg d'eau à 100 °C : on obtient 100 kg de vapeur d'eau à cette température.

La chaleur latente de vaporisation de l'eau est l'énergie qu'il faut fournir pour vaporiser 1 kg d'eau prise à 100 °C

Q3 = m Lv.

Q= Q1 +Q2 +Q3 = m[ Lf+ c Dq + Lv]=Q= 10 [335+4,185*100 + 2 225]= 2978 kJ.

 




retour -menu