d'après concours ESIEE 2006

Aurélie 05/04/06

D'après concours ESIEE 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Radioactivité.

On considère la réaction de fission suivante : ²³⁵₉₂U +¹₀n---> ¹⁴⁶₅₈Ce +⁸⁵₃₄Se+5¹₀n
On donne m(²³⁵₉₂U) = 234,993 u ; m(¹⁴⁶₅₈Ce) = 145,878 u ; m(⁸⁵₃₄Se)= 84,903 u ; m(¹₀n) = 1,008 u ; m(¹₁p) = 1,007 u ;
1 u= 5/3 10^-27 kg ; 1 eV= 5/3 10^-19 J ; N_A= 6 10²³ mol^-1 ; 1TEP= 40,5 10⁹ J ; c= 3 10⁹ m/s.
A- La perte de masse de la réaction est 0,180 u vrai
Dm= m(¹⁴⁶₅₈Ce) +m(⁸⁵₃₄Se)+ 4 m(¹₀n) - m(²³⁵₉₂U)=145,878+ 84,903+4*1,008 - 234,993 = -0,18 u = -0,18*5/3 10^-27 =-0,3 10^-27 kg.
B- La réaction libère 16,2 10¹² J par kg d'uranium 235.faux
Dmc²=0,3 10^-27 *9 10¹⁶ =2,7 10^-11 J par réaction ; 2,7 10^-11 N_A= 2,7 10^-11 *6 10²³ =1,62 10¹³ J par mole d'uranium ; 1,62 10¹³/235*1000=6,9 10¹³ J par kg d'uranium 235.
C- Le défaut de masse de²³⁵₉₂U est de 143 u.faux
Dm= 92m(¹₁p) + (235-92)m(¹₀n) - m(²³⁵₉₂U)=92*1,007+143*1,008-234,993 =1,79 u.
D- Le noyau de ⁸⁵₃₄Se contient 85 neutrons faux 85-34 neutrons
E- 400 TEP fournissent autant d'énergie que 1 mol d'uranium 235.vrai
1,62 10¹³ J par mole d'uranium ; 400 TEP= 400*40,5 10⁹ = 1,62 10¹³ J
Pour dater un morceau de bois ancien, on utilise la méthode de datation au carbone 14. Pour cela on dispose de l'activité du bois ancien, mesurée aujoud'hui , 2Bq ; de l'activité d'un morceau de bois récent analogue mesurée aujourd'hui 4 Bq ; l'évolution de l'activité de ce type de bois en fonction du temps :
A- Le temps de demi-vie du carbone 14 est 6000 ans. vrai
B- Pour le bois récent on mesure 240 désintégrations par minute. vrai 4 désintégrations / seconde soit 4*60 = 240 désintégrations / min.
C- Le bois ancien date d'environ 6000 ans. vrai l'activité est divisée par deux pendant un temps égal à une demi-vie.
D- Dans 6000 ans le bois ancien présentera 2 fois moins de désintégrations qu'aujourd'hui. vrai
E- Dans 12000 ans le bois ancien contiendra encore 12,5% de carbone 14 initial. vrai l'activité est divisée par 2³ pendant un temps égal à trois demi-vie 6000 + 12000 = 3 demi-vie).

Chute, cinématique, pendule, projectile

On lâche d'une altitude h une masse m=200 g supposée ponctuelle avec une vitesse initiale v₀, orienté vers le bas, de valeur 2 m/s. On néglige tout frottement. g= 10 m/s². Le temps de chute de m est de 2 s.
A- h=20 m. faux. Suivant un axe vertical orienté vers le bas : h=½gt²+v₀t = 5t²+2t ; h = 5*2²+2*2 = 24 m.
B- Au bout d'une seconde "m" a parcouru ½h. faux h=½gt²+v₀t = 5t²+2t ; h = 5*1²+2*1 = 7 m au bout d'une seconde de chute.
C- La vitesse d'arrivée au sol est 22 m/s. vrai ; v = gt+v₀ = 10 t + 2 = 10*2+2 = 22 m/s au sol.
D- A l'altitude ½h la vitesse vaut 12 m/s. faux ; v² -v²₀ = 2g(½h) ; v² =v²₀+ 2g(½h) =2²+10*24 = 244 ; v= 15,6 m/s
E- m atteint la vitesse de 12 m/s au bout d'une seconde. vrai ; v = gt+v₀ = 10 t + 2 = 10*1+2 = 12 m/s à t=1 s.
Max et Léon se rendent chez Jules en métro. Jules habite entre les stations S₁ et S₂ distantes de 1 km, plus précisément à 550 m de S₁. Max et Léon empruntent la même rame de métro mais Max descend à la station S₁ et Léon à la station suivante S₂. Entre chaque station, le métro démarre avec une accélération g=1 m/s² jusqu'à atteindre la vitesse de 36 km/h qu'il garde pendant un certain temps, puis il décèlère avec g '= -1 m/s² jusqu'à l'arrêt. Dès que Max et Léon sortent du métro, ils marchent à la vitesse constante de 6 km/h
A- Le métro parcourt la distance S₁S₂ en 1 min 50 s.vrai
démarrage du métro : 36 km/h = 36/3,6 = 10 m/s ; v= g t soit t =10 s ; v²=2gx soit x= v²/(2g) =100/2 = 50 m parcouru pendant la phase de démarrage en 10 s.
arrêt du métro : v= g t + v₀ = -t+10 ; durée de cette phase t = 10 s ; distance parcourue x= -½gt²+v₀t =-0,5t² + 10 t = -50+100 = 50 m
Le métro parcourt 900 m à la vitesse de 10 m/s ; durée de cette phase : 90 s ; durée totale 110 s = 1 min 50 s.
B- Léon arrive chez Jules avant Max. faux
Léon doit parcourir 450 m à 6/3,6 =5/3 m/s ; durée = 450*3/5 = 270 s ; il faut ajouter la durée du parcours en métro (110 s) d'où : 380 s = 6 min 20 s.
Max parcourt 550 m à 5/3 m/s soit une durée de 550*3/5 = 330 s
C- Léon arrive chez Jules 6 min 20 s après avoir quitté Max à la station S₁vrai.
D- Léon et Max arrivent chez Jules à 50 s d'intervalle. vrai
E- Le métro roule à vitesse constante sur 800 m. faux
Une masse m est attachée à un fil inextensible, sans masse et de longueur L, est lâchée de A sans vitesse initiale. On néglige tout frottement. m oscille dans le plan vertical entre les positions extrèmes A et D. On se place dans le cas des petites oscillations : l'angle q entre le pendule et la verticale reste faible et sinq voisin de q radian. m= 100 g ; L= 25 cm ; g= 10 m/s² ; p²=10 ; q_A=30° ; q _B=15°
A- m atteint D au bout d'une seconde. faux période du pendule T= 2p (L/g)^½ = 6,28 (0,25/10)^½ = 1 s ; durée du parcourt AD : 0,5 s.
B- m passe en C, point le plus bas avec une vitesse de ½ 10^½. faux
écrire la conservation de l'énergie mécanique entre A et C : E(A) = mgL(1-cos30) ; E(C) = ½mv² ; d'où v²= 2gL(1-cos30) = 0,5*10(1-0,87) = 0,5*0,13*10 = 0,67 ; v=0,81 m/s.
C- La norme du vecteur accélération en C est nulle. faux ; le poids n'est pas égal à la tension du fil au point C ; la somme vectorielle des forces n'étant pas nulle, l'accélération n'est pas nulle.
D- m met autant de temps pour parcourir l'arc AB que pour parcourir l'arc BC. faux ; les deux arcs de cercle ont même mesure mais la vitesse sur le parcours AB est bien plus faible que la vitesse sur le parcours BC.
E- Quand m passe en C la tension du fil est égale au poids de m. faux

On lance de O avec une vitesse initiale v₀ inclinée d'un angle a avec l'axe horizontal, une bille de masse m supposée ponctuelle. h=HK est la hauteur maximale atteinte par le projectile et p=OA la portée. On néglige tout frottement. On note E_c(X) et E_p(X) respectivement l'énergie cinétique et l'énergie potentielle de pesanteur de m en X. m= 100 g ; h= 10 m ; p/h=4 ; g= 10 m/s².

A- tan a=1 vrai ; flèche h = v²₀ sin²a/(2g) ; portée p= v²₀ sin(2a)/g ; p/h =4 / tana = 4 ( a =45°)
B- v₀ = 20 m/s vrai ; h = v²₀ sin²a/(2g) ; v²₀ = 2gh/sin²a = 200/sin²a ; v₀ =1,414*10 / sin 45 = 20 m/s.
C- E_c(K)=0 faux ; la composante horizontale de la vitesse n'est pas nulle en K mais vaut v₀ cosa.
D- E_c(A)= 20 J vrai ; la variation d'énergie cinétique est nulle entre O et A ( O et A sont dans le même plan horizontal, le poids ne travaille pas) ; l'énergie cinétique en A est égale à l'énergie cinétique en O soit ½mv²₀ = 0,5*0,1*20² = 20 J
E- E_p(A)-E_p(K)=10 J faux ; énergie potentielle en K : mgh = 0,1*10*10 = 10 J ; O est prise comme origine de l'énergie potentielle ;
E_p(A)-E_p(K)= -10 J.

oscilateur, chute dans un liquide, satellite

Une masse m est attachée à l'extrémité d'un ressort, sans masse, de constante de raideur k et de longueur à vide l₀. L'autre extrémité est fixée en O à un support immobile. On néglige tout frottement. On lâche m sans vitesse de A. m oscille en restant sur l'axe Ox entre les positions A et B. Ox est orienté vers le bas. m= 100 g ; k = 5 N/m ; l₀ = 80 cm ; x(A) = 1,2 m.
A- x(B) = 80 cm. vrai ; longueur du ressort à la position d'équilibre : k(l -l₀)=mg soit l -l₀= mg/k = 0,1*10/5 = 1/5 = 0,2 m ; A et B sont symétriques par rapport à la position d'équilibre.
B- m effectue des oscillations en moins d'une seconde. vrai ; période T²= 4p² (m/k) =40*(0,1/5) =0,8 s² ; T voisin 0,9 s.
C- m passe en I milieu de [AB] avec une vitesse de 2^½ m/s vrai
écrire la conservation de l'énergie mécanique : E(A) = ½k IA² ; E(I)= ½mv² soit v²= kIA² / m = 5*0,2²/0,1 = 2
D- En B l'énergie potentielle élastique de m est nulle vrai ; en B le ressort n'est pas déformé, mais tout dépend du choix de l'origine de l'énergie potentielle élastique ; cet origine est très souvent prise à l'équilibre statique du système {ressort + masse m}
E- Quand m passe en I la tension du ressort est égal au poids de m. vrai.
x(t) = 0,2 cos (wt)+1 ; x"(t) = -w² x(t) =-0,2 w² cos (wt) ; en I , cos (wt) = 0 , l'accélération est nulle et d'après la seconde loi de Newton poids et tension ont même valeur.
A l'instant t=0 on lâche à partir de O et sans vitesse initiale une bille de masse m, de petites dimensions, pleine ( masse volumique r) dans un fluide de masse volumique r '. Outre son poids et la poussée d'Archimède A la bille est soumise à une force de frottement fluide de valeur kv , où k est une constante, v la vitesse ( cette force colinéaire à la vitesse est de sens contraire à la vitesse ). Le récipient est suffisamment grand. m=20 g ; k= 20 SI ; r'/r =0,4.
A- L'équation différentielle vérifiée par la vitesse est dv/dt + kv/m =g (r-r')/r. vrai
Sur un axe vertical orienté vers le bas, écrire la seconde loi de Newton : r V g-r'Vg -kv = mdv/dt = r Vdv/dt ; V : volume du solide de masse m ;dv/dt +kv/m = g( r-r') /r.
B- La vitesse de m tend vers la valeur 0,06 m/s. faux
vitesse limite r V g-r'Vg -kv_l =0 ; r V g-r'Vg =kv_l ; v_l = gV(( r-r'))/k ; avec V= m/r ; v_l = mg( r-r')/(kr) ;
v_l = mg( 1-r'/r)/k = 0,02*10*0,6/20 = 0,006 m/s
C- La bille constitue un système conservatif. faux
D- k s'exprime en kg s^-1. vrai ; kv s'exprime en newton (N) soit kg m s^-2 ; v s'exprime en m s^-1 ; k= force / vitesse s'exprime en kg s^-1
E- A= 0,08 N vrai ; A = r'Vg = r'm/r g = 0,4*0,02*10 = 0,08 N
Un astre A sphérique, de rayon R_A= 5000 km, possède un satellite stationnaire S, c'est à dire restant constamment au dessus du même point de l'astre. On connaît la durée du jour sidéral de A, T_A= 2 10⁴s et le champ de pesanteur à la surface de A, g_A= 4 m/s².
A- L'orbite de S appartient au plan équatorial de A. vrai
B- S évolue à 5000 km d'altitude. vrai
3^è loi de Kepler T²/r³ = 4p²/(gR_A²) soit r³ = T²gR_A² / (4p²)= 4 10⁸*4*25 10¹²/40 =10²¹ soir r = 10⁷ m = 10⁴ km ; R_A+h = 10000 km
C- S évolue à la vitesse de 3200 m/s environ. vrai ; v² =gR_A²/r = 4*25 10¹² / 10⁷ = 10⁷ ; v voisin 3200 m/s.
D- Sa période est de 2 10⁴ s. vrai
E- Son vecteur accélération est nul. faux ; accélération centripète de valeur : GM_A/ (R_A+h)²

Une masse m, ponctuelle, est lancée de O avec une vitesse v₀, suivant OA. m parcourt d'abord OA incliné d'un angle a par rapport à l'horizontale puis une portion horizontale à partir de A. m subit une force de frottement , de valeur constante F, colinéaire et de sens contraire au vecteur vitesse. m= 100g ; h= 2 m ; OA= 4 m ; F=0,3 N ; v₀ = 3 m/s.

A- La vitesse ne A vaut 5 m/s. vrai
variation de l'énergie cinétique entre O et A : ½mv²-½mv₀² ; travail du poids de O à A, moteur : mgh ; travail des frottements de O à A : -F OA ; l'action normale du support, perpendiculaire à la vitesse ne travaille pas.
écrire le théorème de l'énergie cinétique : ½mv²-½mv₀² = mgh-F OA ; v² = v²₀+2gh-2F OA/m = 9+20*2-2*0,3*4/0,1 =25 ;
B- m parcourt OA en 0,8 s. faux
sur un axe orienté de O vers A, écrire la seconde loi de Newton : mg sin a -F = ma soit a = g sin a -F/m = gh/OA-F/m = 20/4-0,3/0,1 = 2 m/s²
OA = ½at²+v₀t =t²+3t = 4 ; résoudre t²+3t-4=0 ; t = 1 s.
C- m s'arrête en B tel que OB= 3 m. faux
écrire le théorème de l'énergie cinétique sur la parite horizontale entre A et B : 0-½mv² = -F AB ; AB = mv²/(2F) = 0,1*5²/0,6=25/6
D- Le travail de la force de frottement entre A et B vaut -1,25 J vrai
-F AB = -0,3*25/6 = -1,25 J
E- Le travail du poids entre O et A vaut 4 J. faux mg h= 0,1*10*2 = 2 J

Dipôle RLC.

Le circuit RC est alimenté par un générateur de tension constante E₀.

Lors de la charge du condensateur :

A- Le courant i à l'allure de la courbe 1. faux ; courbe 2
B- La tension u_c à l'allure de la courbe 2. faux ; courbe 1
C- A la fin de charge le condensateur a emmagasiné l'énergie ½CE²₀. vrai
Lors de la décharge du condensateur ( position O de l'interrupteur)
D- Le courant i à l'allure de la courbe 3. vrai
E- La tension u_c à l'allure de la courbe 4. faux
Le circuit RL est alimenté par un générateur de tension constante E₀.
Lors de l'établissement du courant ( K fermé)
A- Le courant i à l'allure de la courbe 1. vrai
B-La tension u_L à l'allure de la courbe 2.vrai
Lors de l'interruption du courant ( K ouvert)
C- Le courant i à l'allure de la courbe 3 faux courbe 2
D- La tension u_L à l'allure de la courbe 4. faux courbe 3
E- La tension aux bornes de R a toujours la même allure que i. vrai
intensité qui traverse le résistor et tension aux bornes du résistor sont proportionnelles.
Un circuit LC est parcouru par un courant i(t)= 0,005 sin ( 1000t) exprimé en ampère. L= 0,1 H. On note q(t) la charge du condensateur à l'instant t.
A- La fréquence du courant est 1000 Hz. faux 1000 = 2p f
B- C= 10 mF. vrai période au carré T² = 4 p² ( LC) soit C = T² / (4 p² L) avec T= 2p/1000 ; C= 10^-6 / L = 10^-5 F
C- |q(0)|=5 10^-6 C.vrai
i(t) = dq(t) /dt donc la charge est une primitve de l'intensité : q(t) =-0,005/1000 cos(1000t) ; q(0) = - 10^-6 C ; |q(0)|= 5 10^-6 C.
D- u(t) = 0,5 cos (1000t) vrai
u(t) = q(t) / C = 5 10^-6 cos(1000t) /10^-5 =0,5 cos(1000t)
E- q(t) = 5 10^-6[1-cos(1000t)] faux
Un dipôle RLC série est soumis à une tension sinusoïdale e(t) et parcouru par un courant i(t). C= 5 10^-6 F.
A- R= 250 W vrai ; R= 5/ 2 10^-2= 250 ohms.
B- L=20 mH vrai
période T= 2 10^-3 s (lecture fraphe) ; T²= 4 p² ( LC) soit L = T² / (4 p² C) = 4 10^-6 /(40 *5 10^-6) = 0,02 H
C- Le circuit est à la résonance vrai i(t) et e(t) sont en phase.
D- La puissance moyenne du circuit sur une période vaut 100 mW. faux intensité efficace =I_eff = 2 10^-2 / 2^½ ; tension efficace =U_eff = 5 / 2^½ ; puissance consommée I_effU_eff=0,05 W = 50 mW
E- La puissance dissipée par effet joule est nulle. faux RI²_eff

Ondes.

Une source sonore émet deux sons brefs espacés d'un temps T. Ces sons sont enregistrés sur un oscillographe sur deux voies différentes ( même échelle sur les deux voies) à l'aide de deux microphones A et B, alignés avec la source. On note d la distance entre les deux microphones et on donne la célérité du son dans l'air v_son = 1000/3 m/s, supposée constante.
A- La voie 1 correspond au microphone le plus proche de la source.vrai
B- T= 5 ms. faux 12 div soit 12 ms entre deux sons brefs.
C- T= 12 ms. vrai 12 div soit 12 ms entre deux sons brefs
D- d= 1,66 m vrai ; d = v_son T = 1000/3* 5 10^-3 = 5/3 m
E- d= 4 m faux
A- Une onde sonore est transversale. faux longitudinale
B- La vitesse du son dans le vide se rapproche de la célérité de la lumière. faux pas de propagation du son dans le vide
C- La vitesse du son dans l'eau est supérieure à celle dans l'air. vrai
D- La longueur d'onde des ondes sonores est comprise entre 400 et 800 nm. faux cet intervalle est celui des ondes lumineuses du domaine visible.
E- La fréquence d'une onde sonore dépend du milieu traversé. faux la fréquence caractérise une onde, et ne dépend pas du milieu.

On observe sur un écran la figure de diffraction d'un faisceau laser de longueur d'onde l par un fil de diamètre a situé à la distance D = 2 m de l'écran.

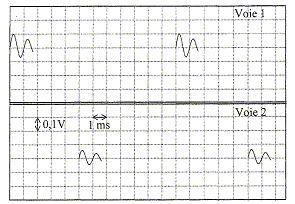
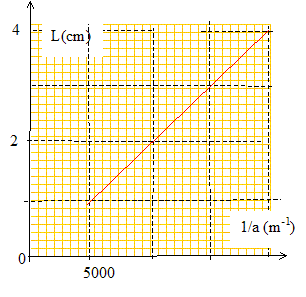
Le graphe ci-dessous représente la largeur L de la tache centrale en fonction de 1/a.

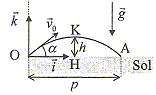
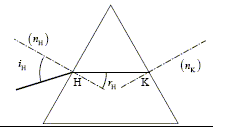
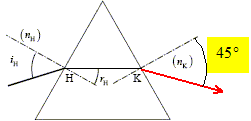
L'écart angulaire q sous lequel est vu la moitié de la tache centrale depuis l'objet diffractant est supposé petit.

A. l = 500 nm. vrai.

q = l/a = L/(2D) ; L =2Dl * (1/a) ; le coefficient directeur de la droite ci-dessus est égal à 2Dl = 0,01 /5000 = 2 10^-6 m².

d'où l = 2 10^-6 /4 = 5 10^-7 m = 500 nm.

B. q est proportionnel à a. faux.

C. pour a = 800 mm, L= 1,6 cm. faux.

aL =2Dl =2 10^-6 m² d'après le graphe.

800 10^-6 *1,6 10^-2 =12,8 10^-6, valeur différente du coefficient directeur.

D. pour a = 100 mm, q = 5 10^-3 rad. vrai.

q = l/a =5 10^-7 / 100 10^-6= 5 10^-3 rad.

E. pour L = 2 cm, q = 10^-2 rad. faux.

q = l/a = L/(2D) = 0,02 / 4 =5 10^-3 rad.

Un faisceau lumineux incident traverse en H et K un prisme équilatéral. Lorsque iH= 45 ° le faisceau HK est horizontal. L'indice de l'air est égal à 1.

A. l'indice du prisme vaut 1,3. faux.

Loi de Descartes pour la réfraction en H : sin 45 = n sin r_H avec r_H = 30° ; sin 30 = 0,5

n = 0,707/0,5 =1,41.

B. pour i_H=45°, le rayon sortant en K et le rayon incident ont la même direction. faux.

Loi de Descartes pour la réfraction en K : n sin 30 = sin r_K par suite i_K=45°.

C. pour i_H = 40,5°, r_H~30°.faux.

D. pour i_H = 90°, r_H~45°. vrai.

Loi de Descartes pour la réfraction en H : sin 90 = 1,41 sin r_H ; sin r_H = 1/1,41 = 0,707 ; r_H~45°.

E. il existe un angle i_H pour lequel on observe aucune réfraction. faux.

Cela ne peut pas se produit quand on passe de l'air dans un verre, milieu plus réfringent que l'air.

On réalise le titrage pHmétrique de 100 mL d'un acide AH par la soude NaOH à 0,02 mol/L. Au point équivalent on a versé 150 mL de soude et le pH vaut 8.

A. la constante d'équilibre de la réaction s'écrit :[A^-][H₃O⁺] / [AH]. faux.

AH + HO^- = A^- +H₂O ; K = [A^- ] / ([HO^- ][AH]).

B. la constante d'acidité s'écrit :[A^-][H₃O⁺] / [AH]. vrai.

C. la concentration initiale de la solution de AH est 0,03 mol/L. vrai.

A l'équivalence C_AV_A = C_BV_B ; C_A= C_BV_B / V_A =0,02*150/100 = 0,03 mol/L.

D. au point équivalent [A^-]= [AH]. faux.

Cela n'est vrai qu'à la demi-équivalence.

E. au point équivalent [Na⁺]=0,02 mol/L. faux.

Il faut prendre en compte la dilution [Na⁺] = C_BV_B /(V_A+V_B) = 0,02*150/250 =0,012 mol/L.

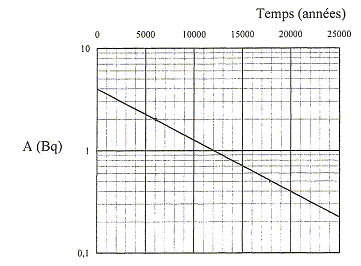
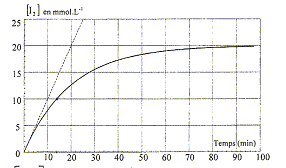
On étudie la cinétique de l'oxydation des ions iodure I^- par l'eau oxygénée H₂O₂. L'équation bilan de la réaction s'écrit : H₂O₂ + 2I^-+ 2H⁺ = I₂+2H₂O. Les concentrations nitiales sont : [I^-]₀=0,05 mol/L ; [H₂O₂]₀=0,03 mol/L ; [H⁺]₀=0,04 mol/L. Les mélanges sont réalisés à t=0 ; La température et le volume du mélange restent constants.

A- Le nombre de mole de I₂ formés au cours du temps est égal au double de mole de I^- disparu. faux
d'après les coefficients de l'équation : n(I^-) disparu = 2 n(I₂) formé.
B- H₂O₂ est le facteur limitant. faux
Soit 1 L de solution ; à partir de 0,03 mol H₂O₂, on peut oxyder 0,06 mol I^- ; or il n'y a que 0,05 mol d'ion iodure ; celui-ci est donc en défaut.
C- Le temps de demi-réaction vaut 14 min. vrai
à t½ l'avancement est égal à la moitié de l'avancement final ; lire l'abscisse correspondante à 10 mmol/L de I₂.
D- A t=0, la vitesse d'apparition du diiode est de 20 mmol L^-1 min^-1. faux
coefficient directeur de la tangente à l'origine ; 20 / 20 = 1 mmol L^-1 min^-1.
E- Lorsque t tend vers l'infini, [I^-] tend vers 0,01 mol/L. vrai
Soit 1 L de solution ; n(I₂)_oo=20 mmol ; n(I^-)_disparu= 40 mmol ; n(I^-)_oo= 50-40 = 10 mmol

retour -menu