|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
|
|
|
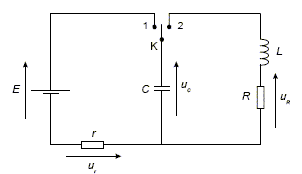
Partie 1 : on s'intéresse à la charge du condensateur de capacité C par un générateur de tension de fem E. A l'instant t=0 on place l'interrupteur en position 1'. L'évolution au cours du temps de la tension uc aux bornes du condensateur et de la tension uR aux bornes du conducteur ohmique de résistance r est représentée ci-dessous : 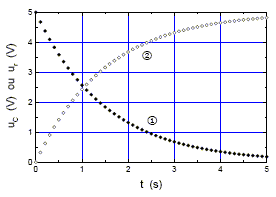
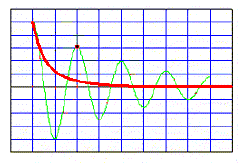
Partie 2 : on suppose maintenant que le condensateur a acquis sa charge maximale. On place alors l'interrupteur K en position '2'. On observe, à l'aide d'un oscilloscope, la tension uC sur la voie A et la tension uR sur la voie B. 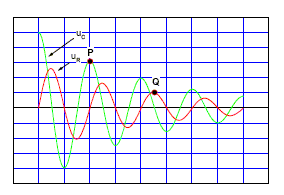 balayage horizontal : 5 ms/div ; voie A : 1 V/div ; voie B : 250 mV/div.
corrigé La courbe 2 illustre l'évolution de uc : la tension aux bornes du condensateur croît exponentiellement de puis 0 jusqu'à une valeur limite lors de la charge. charge q du condensateur à la fin du processus de charge : q=CE= 50 10-6*5 = 2,5 10-4 C valeur de t : lecture graphique ( courbe 2) de l'abscisse correspondant à l'ordonnée 0,63*5 = 3,15 V ; t voisin 1,4 s intensité à l’instant t = t : lecture graphe ( courbe 1) de l'ordonnée correspondante à t=t =1,4 s. ur= 2 V avec r = 30 kW d'où i = 2/3 104 = 6,7 10-5 A énergie emmagasinée à tout instant par le condensateur : Ec=½Cu²c ; par la bobine : EL=½Li² point P : uc= 3 V ; uR=0 donc i=0 et EL=0 ; Ec=½ *50 10-6*9 = 2,25 10-4 J. point Q : uc= 0 V donc Ec=0 ; uR=0,25 V soit i= 0,25/5 = 0,05 A donc EL=½ *0,05*0,05² = 6,25 10-5 J. une grande partie de l'énergie est dissipée par effet joule dans R entre les dates correspondantes aux points P et Q si R est suffisamment grande, on n'observe plus d'oscillations : système apériodique.
|
||
|
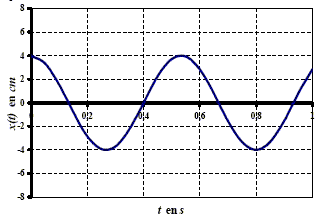
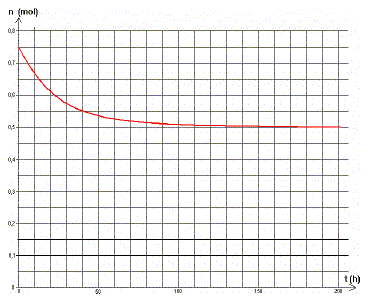
Un capteur fixé sur la bouée n°1 permet d'enregistrer le mouvement vertical de la surface de la mer dû à la houle. Ce capteur a permis de réaliser l'enregistrement présenté ci-dessous, débutant à un instant choisi comme origine ( t=0). 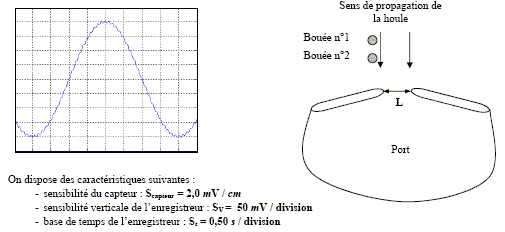
corrigé “période spatiale” d’une onde : longueur d'onde exprimée en m. période (temporelle) de cette houle : lecture graphe : 8 divisions soit T= 8*0,5 = 4 s. vitesse de propagation de cette houle : longueur d'onde l=24 m v = l/T= 24/4 = 6 m/s. amplitude de cette houle : lecture graphe : 8 divisions crête à crête soit 2A= 8*0,05 = 0,4 V = 400 mV puis prendre en compte la sensibilité du capteur 2 mV/cm d'où : 2A=200 cm = 2 m ; A= 1,0 m capteur déclenché à l'instant t1=3 s ; enregistrement avec un second capteur :
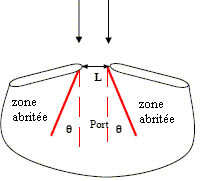
phénomène se produisant à l'entrée du port dont la largeur est du même ordre de grandeur que la longueur d'onde : diffraction
q= l/L =24/48 = 0,5 rad
|
||
|
|