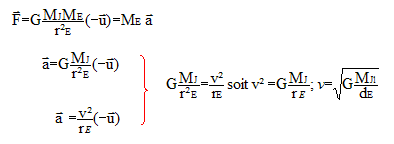Aurélie 25/11/06

Satellites de Jupiter ; oscillation d'une passerelle ; circuit RLC : d'après concours EMIA 2005 ( école militaire interarmes)

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


Satellites de Jupiter : (4 points)

Données : valeurs arrondies pour faciliter les calculs

G= 7 10-11 kg m3 s-2 ; rayon de l'orbite du satellite Europe : rE= 7 105 km ; période de révolution du satellite Europe autour de Jupiter : TE= 3 105 s ; masse de la Terre : MT= 6 1024 kg.

  1. Représenter sur un schéma la force exercée par Jupiter sur Europe et donner l'expression de sa valeur.
  2. Enoncer le principe des actions réciproques ou troisième loi de Newton. Que peut-on en déduire pour Jupiter et Europe ?
  3. Définir un mouvement circulaire uniforme puis donner les caractéristiques du vecteur accélération d'un point mobile qui subit un tel mouvement.
  4. Le mouvement du satellite Europe est décrit dans un référentiel jupitérocentrique. Par analogie avec le référentiel géocentrique, donner les caractéristiques du référentiel jupitérocentrique.
  5. Montrer que si l'orbite du satellite Europe est circulaire, le mouvement de son centre d'inertie est uniforme et démontrer que la vitesse de son centre d'inertie est v= (GMJ / rE)½.
  6. Démontrer que le rapport TE2/rE3 ne dépend que de G et de la masse de Jupiter. Que retrouve t-on avec ce résultat ?
  7. Estimer l'ordre de grandeur de la masse de Jupiter et comparer la valeur obtenue à la masse de la Terre.

 

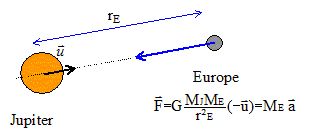
corrigé
force exercée par Jupiter sur Europe et expression de sa valeur :

principe des actions réciproques ou troisième loi de Newton :

Interaction entre un objet A et un objet B : si un solide noté A exerce sur un solide noté B une force notée F A / B, alors B exerce sur A une force notée F B / A . Les deux forces associées à une même interaction ont même valeur et sont opposées.

valeur de FJ/E = valeur de FE/J.

mouvement circulaire uniforme :

la trajectoire est un cercle ; la valeur du vecteur vitesse est constante.

caractéristiques du vecteur accélération d'un point mobile qui subit un tel mouvement :

accélération centripète ( dirigée vers le centre du cercle) ; valeur a= v²/R ( R : rayon du cercle ; v : vitesse )

Le mouvement du satellite Europe est décrit dans un référentiel jupitérocentrique.

caractéristiques du référentiel jupitérocentrique : lié à Jupiter.

origine du repère : centre de Jupiter ; les trois axes pointent vers des étoiles lointaines qui semblent fixes.

l'orbite du satellite Europe est circulaire.

Montrons que le mouvement de son centre d'inertie est uniforme :

Europe n'est soumis qu' à la force de gravitation de Jupiter ; cette force est centripète ; la vitesse du satellite Europe est perpendiculaire à la force.

La force de gravitation ne travaille pas ; elle ne modifie pas l'énergie cinétique : la valeur de la vitesse est donc constante.

Le mouvement est uniforme.

Expression de la vitesse de son centre d'inertie :

Montrons que le rapport TE2/rE3 ne dépend que de G et de la masse de Jupiter :

La période de révolution TE du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme.

2 p rE =vTE

élever au carré, puis remplacer v² par l'expression ci dessus.

4p² rE² = v² T²E = GMJ/ rE T²E

ou T²E =4p² /(GMJ) rE3.

soit T²E /rE3 = 4p² /(GMJ) rapport constant pour une planète donnée.(3ème loi de Kepler)

distance en mètre, période en seconde, masse en kg.

Estimation de l'ordre de grandeur de la masse de Jupiter :

MJ = 4p² rE3 / (GT²E )

MJ = 4*3,14² * (7 108)3 / (7 10-11 *9 1010) = 4*10**49 1024 / 0,9 voisin de 2 1027 kg

330 fois plus grande que la masse de la Terre.


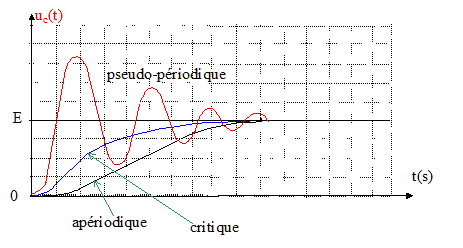
Oscillations d'une passerelle : (3 points)

 Texte extrait d'un article scientifique :

Les passerelles sont mises en vibration par le passage des piètons. Quand le rythme de la marche concorde ave c un fréquence propre de l'ouvrage, ce dernier entre en résonance : les oscillations s'amplifient et peuvent atteindre des niveaux importants. Dans la plupart des projets le confort du piéton est pris en compte. On évalue l'accélération verticale supportée par un piéton puis on la compare à une accélération critique alim traduisant le critère de confort et qu'il est conseillé de ne pas dépasser. On estime que alim = 0,7 m/s².

On considère une passerelle de 30 m de portée : sa structure porteuse est constituée de deux poutres d'acier qui supportent un plateau en bois. La fréquence propre du plateau est donnée par f0 = ½p(C/m)½, m étant la masse totale de la passerelle , C une constante qui dépend des autres caractéristiques de la passerelle. Ici on prend C= 2,6 104 S.I

Le schéma suivant illustre les oscillations de flexion du tablier de la passerelle dans le mode le plus simple : les deux courbes en pointyillés représentent deux positions fléchies extrèmes.

  1. Les oscillations évoquées dans le texte sont-elles libres ou forcées ? Quel est l'excitateur ? Quel est le résonateur ?
  2. Quelle est l'unité de la constante C ?
  3. Pour une dizaine de piétons, on estime m = 1,3 104 kg. On imagine que les piétons marchent au pas cadencé. Calculer la fréquence des pas pour laquelle la passerelle entre en résonance. ( on donne p2½ = 4,4 )
  4. On considère le mouvement vertical d'un point P situé à mi-travée de la passerelle : il peut être assimilé à un mouvement oscillatoire sinusoïdal de période T et d'équation horaire z = zm cos ( 2p/T t +F0) où zm est positive. Nommer les paramètres zm et F0.
    - Donner l'expression de l'accélération az du point P en fonction de zm, F0, T et t.
  5. En déduire l'accélération maximale du point P en fonction de zm et T.
  6. Montrer que si les 10 piétons mettent en résonance la passerelle, l'accélération critique ne sera pas dépasée à conditions que l'amplitude des oscillations reste inférieure à un certain seuil dont on donnera l'expression en fonction de alim , C et m. Calculer numériquement ce seuil.
corrigé
Les oscillations évoquées sont forcées ; les piétons jouent le rôle d'excitateur ; la passerelle joue le rôle de résonateur.

unité de la constante C :

f0 = ½p(C/m)½ ; C= 4 f0² m / p² .

p² est sans dimension ; f0² est l'inverse du carré d'un temps ; m est une masse.

d'où [C]= T-2 M ; C s'exprime en kg s-2.

Pour une dizaine de piétons, on estime m = 1,3 104 kg. On imagine que les piétons marchent au pas cadencé.

Calcul de la fréquence des pas pour laquelle la passerelle entre en résonance : ( on donne p2½ = 4,4 )

f0 = ½p(C/m)½ = ½p(2,6 104/1,3 104)½ = ½p 2½ = ½*4,4 = 2,2 Hz.

On considère le mouvement vertical d'un point P situé à mi-travée de la passerelle : il peut être assimilé à un mouvement oscillatoire sinusoïdal de période T et d'équation horaire z = zm cos ( 2p/T t +F0) où zm est positive.

zm est l'amplitude ( m) et F0 est la phase initiale ( à t=0)
expression de l'accélération az du point P en fonction de zm, F0, T et t :

l'accélération est la dérivée seconde, par rapport au temps, de l'abscisse

z' = dz/dt = -zm2p/T sin ( 2p/T t +F0)

az = z" = -zm(2p/T)²cos ( 2p/T t +F0)

accélération maximale du point P en fonction de zm et T :

valeur maximale de cos ( 2p/T t +F0) : 1 d'où az max = zm(2p/T)²

Montrons que si les 10 piétons mettent en résonance la passerelle, l'accélération critique ne sera pas dépasée à conditions que l'amplitude des oscillations reste inférieure à un certain seuil dont on donnera l'expression en fonction de alim , C et m :

alim = az max = zm(2p/T0)² ; zm = alimT0²/ (4p²)

de plus T0² = 1/ f0² = 4 m /(Cp²) d'où : zm = alim m / (Cp4)

Calcul ce seuil : alim m / (Cp4) = 0,7 *1,3 104 / ( 2,6 104 *3,144)= 0,7/(200) =7/2 10-3 = 0,0035 = 3,5 mm.

Etude d'un circuit RLC : (3 points)

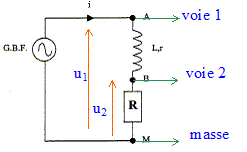
Le générateur basse fréquence délivre une tension sinusoïdale de fréquence 250 Hz et d'amplitude 5 V. La bobine a une inductance L et une résistance r = 12 W ; R= 100 W.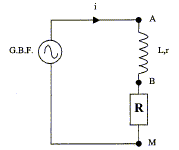

On visualise à l'oscilloscope, voie 1, l'évolution de la tension u1=uAM(t) et sur la voie 2, l'évolution au court du temps de la tension u2 = uBM(t). M est relié à la masse du GBF.

  1. Indiquer les branchements à réaliser pour visualiser u1 et u2.
  2. Exprimer la tension uAB en fonction de u1 et u2 en précisant la loi utilisée.
  3. On remplace l'oscilloscope par un système d'aquisition de données relié à un ordinateur . Un logiciel adapté permet le calcul de u= u1-u2 - ri et permet d'obtenir le graphe donnant l'évolution de u en fonction de di/dt.

    Etablir la relation liant u, L et di/dt.
    Montrer que le graphe 1 permet d'obtenir la valeur de L et calculer une valeur approchée de L.
  4. Association d'un condensateur et de la bobine :
    Dans le circuit précédent on remplace le GBF par un condensateur de capacité C= 1     mF préalablement chargé. On appelle u3(t) la tension aux bornes du condensateur. u3(t) est initialement positive.
    On suppose tout d'abord que la résistance du circuit est faible.
    - Représenter l'allure de la courbe u3(t).
    - Comment appelle t-on le régime libre du circuit RLC obtenu ?
    - Donner une valeur approchée de la pseudopériode de la tension u3(t).( on donne     p10½=10 et p /10½=1 )
    - On augmente progressivement la valeur de R. Quels sont les deux autres régimes libres observés ?     

 

corrigé
branchements à réaliser pour visualiser u1 et u2 :

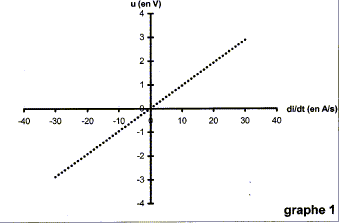
Expression de la tension uAB en fonction de u1 et u2 :

additivité des tensions : uAB = uAM+uMB ; uAB =uAM-uBM = u1 - u2.

On remplace l'oscilloscope par un système d'aquisition de données relié à un ordinateur . Un logiciel adapté permet le calcul de u= u1-u2 - ri et permet d'obtenir le graphe donnant l'évolution de u en fonction de di/dt.

relation liant u, L et di/dt :

u1 = Ldi/dt + (R+r) i ; u2 = R i

u1 - u2 = Ldi/dt + ri ; u = u1-u2 - ri = Ldi/dt

le graphe de u=f(di/dt) est une droite de coefficient directeur L


D'après le graphe 1, L = 2/20 = 0,1 H

Association d'un condensateur et de la bobine :
Dans le circuit précédent on remplace le GBF par un condensateur de capacité C= 1 mF préalablement chargé. On appelle u3(t) la tension aux bornes du condensateur. u3(t) est initialement positive.
On suppose tout d'abord que la résistance du circuit est faible.


l'allure de la courbe u3(t) correspond au régime pseudo-périodique
valeur approchée de la pseudopériode de la tension u3(t).( on donne p10½=10 et p /10½=1 )

T= 2p(LC)½ = 2p(0,1 10-6)½ =2p(0,1 )½10-3 = 2 10-3 s.
On augmente progressivement la valeur de R. on observera le régime critique ouis le régime apériodique.

retour -menu