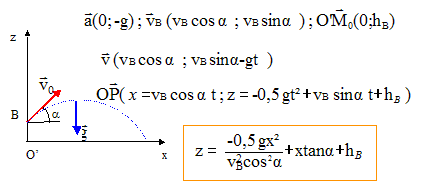Aurélie 10/04/06

Palet propulsé par un ressort

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Palets (7 points)

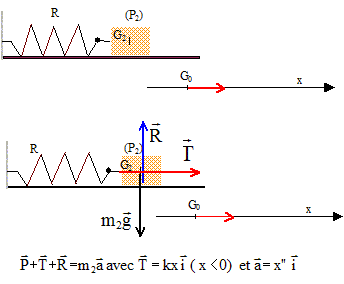
Un palet P1 de masse m1 est propulsé le long d'une piste à coussin d'air. La piste comporte une rampe AB de longueur L inclinée d'un angle a sur l'hotizontale, suivie d'un trou T afin de recevoir ce palet. Le palet P1 est propulsé grâce à un choc avec un palet P2, de masse m2 = 4 m1. Le palet P2 est lui même relié à un ressort R horizontal, de masse négligeable et de constante de raideur k. L'autre extrémité du ressort est fixe en O.

A l'équilibre, la position du centre d'inertie du palet P2 est notée G0 telle que OG0 = l0.

Tous les frottements sont négligés ; Lors du choc le palet P2 transmet intégralement son énergie cinétique au palet P1 ; le ressort exerce une force proportionnelle à sa déformation.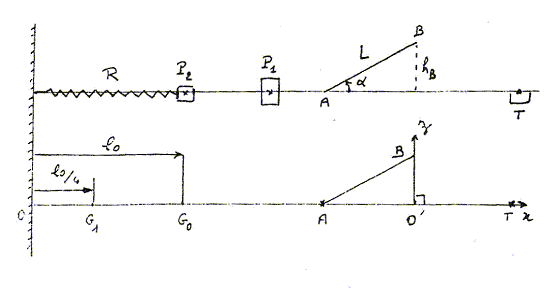

Etude du mouvement du palet P2 :

Un joueur comprime le ressort : la nouvelle position du centre d'inertie G2 du palet devient G1 telle que OG1 = 0,25 l0. Puis ce même joueur le lâche à un instant pris comme origine des dates, sans communiquer de vitesse initiale à P2.

  1. Etablir l'équation différentielle du mouvement du centre d'inertie du palet P2. L'origine sur l'axe x'x est G0.
  2. L'équation du mouvement de G2 est : x(t) = A sin (w0t+f) où x est l'abscisse de G2 sur l'axe G0x.
    - Quelle est la nature du mouvement de G2 ?
    - Préciser la signification physique de A, w0, f.
    - Etablir l'expression littérale de w0, de la période T0.
    - Déterminer les valeurs des constantes A et f.
    - En déduire littéralement puis numériquement l'équation horaire x(t)
  3. Donner l'expression littérale de la vitesse v(t) de G2.
    - A quel instant t0, le centre d'inertie G2 du palet passe-t-il en G0 ?
    - Déterminer la valeur de la vitesse lors du passage en G0.
  4. Exprimer l'énergie mécanique du système ressort et palet à un instant t quelconque.
    - Que vaut cette énergie à l'instant t0 ?
    - En déduire la vitesse v0 du palet à l'instant t0. Cette valeur est-elle en accord avec celle trouvée en 3 ?

Etude du mouvement du palet P1 : le choc entre les palets a lieu lorsque le centre d'inertie G2 du palet P2 passe en G0.

  1. Calculer la vitesse v1 acquise par du le centre d'inertie G1 du palet P1 au moment du choc.
  2. En déduire la vitesse vA du centre d'inertie G1 du palet P1 au passage en A.
  3. On prévoit que le palet P1 aborde la rampe avec la vitesse v2 = 3,6 m/s. Vérifier que cette valeur est en accord avec les hypothèses formulées au départ.
  4. Calculer la vitesse vB au passage au sommet de la rampe, sachant que B est situé à une hauteur hB= 25 cm au dessus du plan horizontal passant par A.
  5. Quelle doit être la longueur L de la rampe.
  6. Déterminer l'équation de la trajectoire du centre d'inertie G1 du palet P1au delà de B, dans le repère O'xz.
  7. Déterminer l'expression littérale, puis numérique, de la vitesse du palet P1 retombant sur le sol.
  8. A quelle distance du point O' faut-il percer le trou.

m1 = 50 g ; m2 = 200 g ; k = 20 N/m ; l0 = 24 cm ; g= 10 m/s² ; a= 30°.

aide au calcul : p²=10 ; sin 30 = 0,5 ; cos 30 = 0,87 ; tan30 = 0,58 ; 3,6²= 13 ; 1,4²=2 ; 18²= 324 ; 8*0,87 = 7

corrigé
équation différentielle du mouvement du centre d'inertie du palet P2 :

soit en projection sur G0x : -kx=m2x" ou bien x" + k/m2 x=0

nature du mouvement de G2 : le mouvement ne dure que 1/4 de période , donc rectiligne non uniformement accéléré.

signification physique de A ( amplitude), w0( pulsation) f ( phase à t=0)
expression littérale de w0 = ( k/m2)½ =10 rad/s période T0 = 2p/ w0 =2p ( m2/k)½ = 6,28/10 = 0,62 s.
valeurs des constantes A et f :

à t=0 x(0) = -0,75 l0 = A cosf avec A positif donc f = p et A = 0,75 l0 .
équation horaire x(t) = 0,75 l0 cos(( k/m2)½t+p)=0,18 cos(10t+p)= 0,18 sin(10t-½p)

expression littérale de la vitesse v(t) de G2 : dériver x(t) par rapport au temps

v(t) = -Aw0 sin (w0t+p)
instant t0, le centre d'inertie G2 du palet passe en G0 : x(t0) = 0 soit 0,18 cos(10t0+p)=0 ; 10t0+p= + ou -½p ; t0= p/20 = 0,25 T0 = 0,157 s.
valeur de la vitesse lors du passage en G0 : Aw0 = 0,18 *10 = 1,8 m/s.

énergie mécanique du système ressort et palet à un instant t quelconque : ½kx²+½m2v²= ½kA²
énergie à l'instant t0 : ½m2v0²

conservation de l'énergie mécanique : ½m2v0² =½kA² ; v0² = kA² /m2 ; v0 = A(k/m2)½ =1,8 m/s.

vitesse v1 acquise par du le centre d'inertie G1 du palet P1 au moment du choc :

conservation de l'énergie cinétique :½m2v0² = ½m1v1² ; v1² = m2v0² /m1 = 4 v0² soit v1 = 2v0 = 3,6 m/s

vitesse vA du centre d'inertie G1 du palet P1 au passage en A : aucune force ne travaille entre G0 et A donc vA= v1.

La vitesse v2 = 3,6 m/s prévue est en accord avec les hypothèses formulées au départ.

vitesse vB au passage au sommet de la rampe :

sur la rampe, l'action du plan, perpendiculaire à la vitesse, ne travaille pas ; le travail du poids est résistant en montée et dépend de la différence d'altitude hB = L sin a. ( W= -m1ghB) Ecrire le théorème de l'énergie cinétique entre A et B :

½m1vB² - ½m1vA² = -m1ghB soit : vB² =vA² -2ghB = 3,6²-20*0,25 = 13-5=8 ; vB= 2,8 m/s.

longueur L de la rampe : hB= L sin a soit L =0,25 / 0,5 = 0,50 m.

équation de la trajectoire du centre d'inertie G1 du palet P1au delà de B, dans le repère O'xz :

z = -0,825 x² +0,58 x+0,25

expression littérale, puis numérique, de la vitesse du palet P1 retombant sur le sol :

sur le parcours A I (impact au sol), écrire le théorème de l'énergie cinétique sachant que le poids ne travaille pas ( A et I ont la même altitude) et que l'action du plan est perpendiculaire à la vitesse : aucune force ne travaille et en conséquence la valeur de la vitesse au sol est égale à vA.

ou bien : v²= [vBcos a)2+ (vBsins a-gt)2]½. Il faut déterminer t en écrivant qu'au sol z =0 soit 0 = -5t² + 2,8 t +0,25

distance du point O' au trou : écrire qu'au sol z=0 soit -0,825 x² +0,58 x+0,25=0

solution positive à retenir x =1 m.


retour -menu