|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
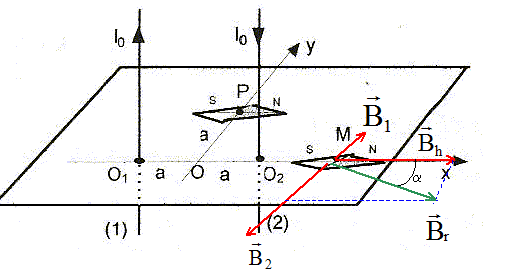
Soient deux fils rectilignes verticaux, infinis, parallèles situés à la distance O1O2 = 2a l'un de l'autre et parcourus par des courants de sens opposé et de même intensité I0. Le plan des deux fils est contenu dans le plan du méridien magnétique terrestre et une aiguille aimantée placée en leur voisinage s'oriente comme sur la figure lorsqu'aucun courant ne traverse les fils. 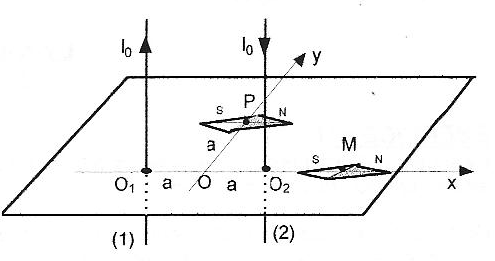 On rappelle qu'un fil rectiligne infini, parcouru par un courant crée en un point M' de l'espace un champ magnétique de valeur B= m0 I/ (2pr), où r est la distance de M' au fil. m0 = 4p 10-7 SI ; 2a = 20 cm ; Bh= 2 10-5 T, composante horizontale du champ magnétique terrestre.
normes B1 et B2 des champs crée en M par les deux fils : O1M=3a et O2M= a B1= m0 I0/ (2p*3a) =Bh/3 ; B2= m0 I0/ (2pa) =Bh.
Br2 =Bh2 +(2/3Bh)2 =13/9 Bh2 ; Br =13½Bh/3 tan a =
(2/3Bh) / Bh = 2,/3 =
0,67 ; a =33,7 °.
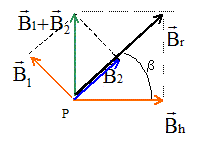
Pythagore : O1P2+ O2P2 =4 a² = O1O22 , donc le triangle PO1O2 est rectangle en P. normes B1 et B2 des champs crée en P par les deux fils : B1=B2= m0 I0/ (2p*2½a) =Bh/2½. schéma en vue de dessus :
Valeur du champ résultant : Br=2½Bh ; tan b = Bh / Bh = 1 ; b =45 °. l'aiguille aimantée tourne de 45°. |
|
|
|