Aurélie 05//06

Chute d'une bille dans l'huile ; d'après concours kiné AP-HP 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.


répondre par vrai ou faux en justifiant ( 8 pts)
  1. Une bille d'acier est lâchée dans un éprouvette contenant de l'huile. Les graduations de l'éprouvette sont repérées en mL, une graduation de 1 mL correspond à une hauteur de 1 cm. L'huile est un liquide de fort coefficient de viscosité. On réalise la chronophotographie du mouvement de cette bille. On obtient le document ci-dessous. L'intervalle de temps entre deux photos est 0,1 s.

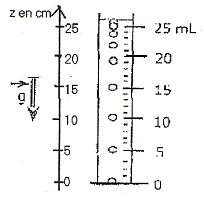
    Le mouvement de la bille dans l'éprouvette est :
    - rectiligne uniforme. Faux , les distances parcourues ne sont pas proportionnelles au temps au début de la chute.
    - rectiligne accéléré. Faux , au bout d'un certain temps, les distances parcourues sont proportionnelles au temps.
    - rectiligne uniformément accéléré. Faux , au bout d'un certain temps, les distances parcourues sont proportionnelles au temps.
    - rectiligne accéléré puis uniforme. Vrai.

  2. La vitesse de la bille lors de cette chute verticale :
    - n'est jamais atteinte. Faux , au bout d'un certain temps, les distances parcourues sont proportionnelles au temps.
    - est de l'ordre de 0,5 m/s. Vrai 5 cm =0,05 m parcouru en 0,1 s soit 0,05/0,1 = 0,5 m/s
    - ne peut pas être calculée par cette méthode.Faux
    - est de l'ordre de 5 cm/s.Faux
  3. L'allure de la courbe des variations de la vitesse en fonction du temps est donnée par :

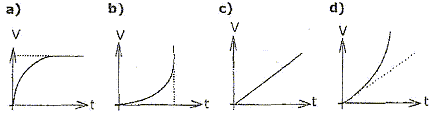
    a) la vitesse croît puis attaint une valeur limite constante ( asymptote horizontale )
  4. Les forces extérieures exercées sur la bille dans le référentiel terrestre sont :
    - le poids et la poussée d'Archimède.
    - le poids.
    - le poids et la force de frotement .
    - le poids, la poussée d'Archimède et la force de frottement. Vrai.

  1. Si le régime asymptotique est atteint, l'équation vectorielle du mouvement est alors :

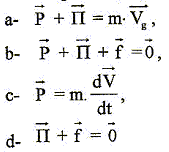
    b) vrai : le poids compense la poussée d'Archimède et la force de frottement quand la vitesse limite est atteinte. Le principe d'inertie affirme que la bille est pseudo-isolée.
  2. On assimile l'action de l'huile sur la bille à une seule force de frottement de valeur f= kv². On suppose négligeable la poussée d'Archimède exercée par l'huile. Dans ces conditions :
    - l'équation différentielle du mouvement est : mdv/dt -mg +kv²=0.     Vrai 2ème loi de Newton écrite sur l'axe vertical orienté vers le bas mdv/dt = mg - kv²
    - dv/dt = g(1-v/v1) si v1 = (mg/k)½. Faux dv/dt = g-kv²/m avec k/m = g/v1².
    - v1 = (mg/k)½ est la vitesse limite de la bille.     Vrai le poids neutralise les frottement si la vitesse limite v1 est atteinte : mg = kv1².
    - la courbe donnant les variations de la vitesse de la bille est une parabole.     Faux une portion d'exponentielle dans sa première partie.
  3. La masse de la bille est m=50 g ; le coefficient de frottement est k= 2 N s² m-2 ; la vitesse limite de la bille dans le champ de pesanteur g= 10 m/s² est :
    - vlim = mg/k = 0,25 m/s.
    - vlim =(mg/k)½= 0,5 m/s Vrai : (0,05*10/2)½=0,25½=0,5 m/s.
    - vlim =mgk= 1,0 m/s.
    - vlim =½mgk= 0,5 m/s.
  4. Si on remplace la bille par une petite bille de polystyrène, cette dernière : la bille de polystyrène va flotter à la surface du liquide ; elle est soumise à son poids et à la poussée d'Archimède.
    - est soumise à l'accélération de la pesanteur. Vrai
    - admet la même accélération que la bille d'acier. Faux
    - est soumise aux mêmes forces que la bille d'acier. Faux
    - admet un mouvement de même nature que la bille d'acier. Faux



retour -menu