Aurélie 05/06
d'après concours manipulateur électroradiologie médicale AP Paris 2003

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

Mécanique : plongeon (4 pts)

 A un instant choisi comme origine des dates, un plongeur de masse m=67,5 kg, s'élance de son plongeoir depuis le point O avec une vitesse initiale v0 = 5 m/s, incliné de a=30° par rapport à l'horizontale. Le plongeoir est situé à une hauteur h=8 m au dessus de la surface de l'eau.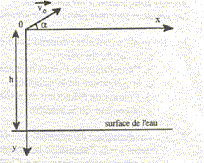

  1. Déterminer l'équation de la trajectoire dans le repère indiqué.
  2. Calculer la durée écoulée entre l'instant où le plongeur quitte le point O et le moment où il entre dans l'eau.
  3. Quelles sont les coordonnées du point où le plongeur touche l'eau ?
  4. Déterminer la valeur de la vitesse du plongeur au moment où il touche l'eau. g= 9,8N/kg.
corrigé
équation de la trajectoire dans le repère indiqué : accélération : (0; g)

vitesse , primitive de l'accélération : ( v0cosa ; gt - v0 sin a )

position, primitive de la vitesse : x= v0cosa t ; y = ½gt²- v0 sin at .

t = x/( v0cosa) ; repport dans l'expression de y : y= ½gx²/(v0cosa)² - x tan a.

y= 4,9 x²/(5 cos 30)² - x tan30 = 0,261 x²-0,577 x.

durée écoulée entre l'instant où le plongeur quitte le point O et le moment où il entre dans l'eau :

résoudre y= 8 soit : 8=4,9 t²-2,5 t ; 4,9 t²-2,5 t-8=0 ; t = 1,56 s.

coordonnées du point où le plongeur touche l'eau :

x= v0cosa t= 5 cos30*1,56 = 6,75 m

y = ½gt²- v0 sin at = 4,9*1,56²-5 sin30*1,56 = 8 m.

valeur de la vitesse du plongeur au moment où il touche l'eau :

vx= v0cosa = 5 cos30 =4,33 ; vy= gt - v0 sin a = 9,8*1,56 -5 sin30 = 12,8 m/s

v² = v²x+v²y=4,33² + 12,8² = 182,6 ; v = 13,5 m/s.
fission( 4 pts)

Dans une centrale nucléaire, une des réactions possibles est représentée par : 23592U+ 10n---> 9438Sr+ 139xXe+y 10n

  1. Calculer les valeurs de x et y en justifiant.
  2. Calculer en eV l'énergie libérée au cours de cette réaction.
  3. L'uranium 235 est radioactif de type a. Le noyau fils obtenu est le Thorium. Ecrire l'équation de cette désintégration.
  4. La demi-vie de l'uranium 235 vaut t½= 4,5 109 ans. Quelle est l'activité de 1,0 g d'uranium 235 ? Préciser l'unité SI.
    masse en u : m(23592U) = 235,0134 ; m(9438Sr) =93,8946 ; m(139xXe) = 138,8882 ; m(neutron) = 1,0087
    1 u =1,67 10-27 kg ; NA= 6,02 1023 mol-1 .
corrigé
23592U+ 10n---> 9438Sr+ 139xXe+y 10n

lois de conservation : conservation de la charge : 92 = x+38 soit x=54

conservation du nombre de nucléons : 235+1=94+139+y soit y=3

énergie libérée par la réaction d'un atome d'uranium 235 :

Dm= m(9438Sr) + m(139xXe) + 3 m(neutron) -m(23592U) = 93,8946 + 138,8882 +2*1,0087- 235,0134 = -0,2132 u

puis -0,2132 *1,66 10-27 = 3,54 10-28 kg

E= |Dm|c² = 3,54 10-28*(3108)² =3,185 10-11 J ou 3,185 10-11 /1,6 10-19 = 1,99 108 eV= 199 MeV

 activité de 1,0 g d'uranium 235 : A= l N

N= masse / masse molaire * NA= 1/235*6,02 1023 =2,56 1021 noyaux d'uranium 235 dans 1 g.

lt½=ln2 soit l =ln2 / t½=ln2 / (4,5 109*365*24*3600) =4,88 10-18 s-1.

A= l N = 4,88 10-18 *2,56 1021=1,25 104 Bq.
lactose (4 pts)

Parmi les constituants du lait, le lactose est l'un des principaux glucides. Ce dernier en présence de bactérie, se dégrade et se transforme en acide lactique de formule semi-développée CH3-CHOH-COOH. La teneur en acide lactique d'un lait est un critère de fraicheur. Si la teneur dépasse 5,0 g/L, le lait caille. Pour un lait frais cette teneur se situe autour de 1,8 g/L. On donne la masse molaire de l'acide lactique M= 90,0 g/mol.

On dose un volume V= 20 mL de lait par une solution d'hydroxyde de sodium de concentration cb=0,10 mol/L. Le volume équivalent est obtenu pour véq = 8,5 mL d'hydroxyde de sodium versé.

  1. Ecrire la formule de la base conjuguée de l'acide lactique.
  2. Ecrire l'équation de la réaction de l'acide lactique avec l'hydroxyde de sodium
  3. Déterminer la concentration molaire de l'acide lactique dans ce lait.
    - En déduire le titre massique de l'acide lactique. Ce lait est-il consommable ? Justifier.
  4. On donne les zones de virage de deux indicateurs colorés. Hélianthine [3,1 - 4,4] et phénolphtaléine [8,2 - 10 ]. Quel est l'indicateur le plus adapté ? Justifier.

 

corrigé
base conjuguée de l'acide lactique : CH3-CHOH-COO-

équation de la réaction de l'acide lactique avec l'hydroxyde de sodium :

CH3-CHOH-COOH + HO- =CH3-CHOH-COO- + H2O

concentration molaire de l'acide lactique :

à l'équivalence du titrage cbvéq= V C soit C= cbvéq/ V=0,1*8,5 / 20 = 0,0425 mol/L (0,042 mol/L)

titre massique (g/L) = concentration molaire ( mol/L) * masse molaire (g/mol) = 0,0425*90 = 3,8 g/L

valeur supérieure à 1,8 g/L, ce lait n'est pas consommable ; de plus il est caillé.

indicateur le plus adapté : à l'équivalence la solution contient une base, l'ion lactate CH3-CHOH-COO- : le pH du milieu est supérieur à 7.
La zone de virage de l'indicateur coloré doit contenir le pH à l'équivalence : donc phénolphtaléine.
Ion iodure et eau oxygénée (4 pts)

On réalise la réaction d'oxydation des ions iodure I-(aq) par une solution d'eau oxygénée. Les couples mis en jeu sont : I2(aq) /I- (aq) ; H2O2/H2O.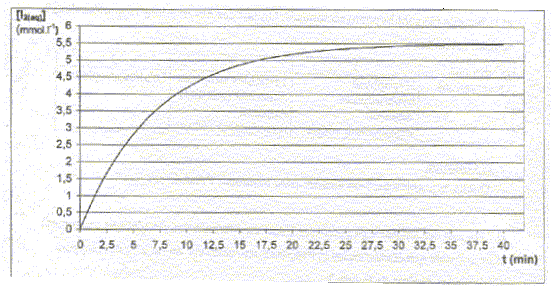

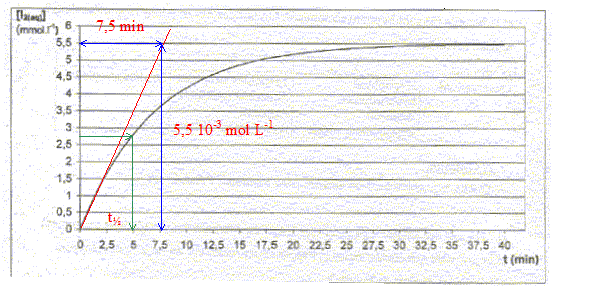
  1.  
  2. Ecrire les demi-équations et l'équation bilan de la réaction.
  3. Définir et calculer la vitesse volumique de réaction à la date t=0.
  4. Comment évolue la vitesse de la réaction ? Justifier.
  5. Calculer le temps de demi-réaction t½.

     

corrigé
demi-équations et l'équation bilan de la réaction :

2I- = I2 + 2e- oxydation ; H2O2+ 2H+ + 2e- = 2H2O réduction

H2O2+ 2H+ +2I- = I2 +2H2O

vitesse volumique de réaction : v= 1/V dx/dt avec x : avancement en mol et V : volume de la solution (L)

si V est constant v = d[I2]/dt

graphiquement, coefficient directeur de la tangente à la courbe ci-dessus, à la date considérée.

v 0=( d[I2]/dt)0 = 5,5 10-3 / 7,5 = 7,3 10-4 mol L-1 min-1.

Evolution de la vitesse de la réaction :

La vitesse de la réaction diminue au cours du temps, car les concentrations des réactifs diminuent : la concentration des réactifs est un facteur cinétique. Graphiquement les tangentes à la courbe ci-dessus se rapprochent de l'horizontale, au cours du temps.

temps de demi-réaction t½ : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final : lecture graphe t½ = 5 min.
retour -menu