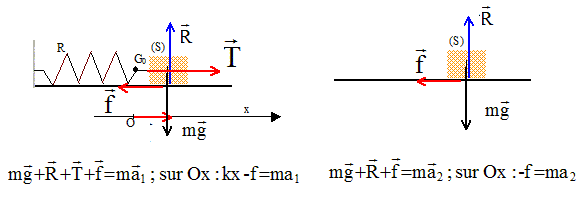Aurélie 05/06
Mécanique : plongeon, rame de métro, chute verticale, ressort

d'après concours manipulateur électroradiologie médicale AP Paris

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

Mécanique : cinématique (4,5 pts)

Partie 1 :

Une rame de métro est soumise dès son départ à une accélération constante g. Au temps t0=0, elle pénètre dans un tunnel avec une vitesse v0 et parcourt à partir de cet instant x1 = 24 m pendant les deux premières secondes (t1). Puis elle parcourt 32 m pendant les deux secondes suivantes. On prendra pour origine des x le début du tunnel.

  1. Etablir les équations horaires de la rame en x1 au temps t1 et en x2 au temps t2.
  2. En déduire et calculer v0 et g.

Partie 2 :

L'accélération est supprimée 10 s après le départ (t3). La rame de métro roule à vitesse constante pendant 30 s (t4).

  1. Calculer la vitesse de la rame à l'instant t3.
  2. Calculer les distances parcourues en t3 et t4.

Partie 3 :

Puis il est soumis à une décélération constante -g jusqu'à l'arrêt à la station suivante.

  1. Calculer la distance parcourue pendant cette phase (t5).
  2. Calculer la distance totale séparant les deux stations.
corrigé
équations horaires de la rame en x1 au temps t1 et en x2 au temps t2 :

v = gt+v0 ; l'abscisse est une primitive de la vitesse x=½gt²+v0 t

x1 = 24 = ½g 2² + 2v0 et x2 = 24+32 = 56 = ½g 4² + 4v0 ;

12=g + v0 et 14=2g + v0 d'où g = 2 m/s² et v0 = 10 m/s

vitesse de la rame à l'instant t3 : v = gt+v0 ; v = 2t+10 = 2*10+10 = 30 m/s.

distance parcourue en t3 : x = ½gt²+v0 t ; x= t²+10t ; x3 = 10²+10*10 = 200 m

distance parcourue en t4 : x4 = x3+ 30*30 = 1100 m

distance parcourue pendant la phase (t5) : on choisit la date t4 comme nouvelle origine des temps et x4 comme nouvelle origine des distances.

x5 = -½*2 t² + 30 t = -t²+30t ; v = -2t+30 d'où la durée avant arrêt : t = 15 s

x5 =-15²+30*15 = -225+450 = 225 m

distance totale séparant les deux stations : 1100+225 = 1325 m.
Mécanique : chute verticale (4 pts)

 

Un enfant lance vers le haut une bille de masse m=30 g. A une hauteur h=1,40 m au dessus du sol, sa vitesse est de 3m/s par rapport au sol. On néglige la résistance de l'air.

  1. Calculer l'énergie mécanique du système {bille-Terre} en prenant l'origine de l'énergie potentielle au sol.
  2. Jusqu'à quelle hauteur la bille va-t-elle monter ?
  3. Avec quelle vitesse va-t-elle repasser à l'altitude h=1,40 m ?
  4. Avec quelle vitesse va-t-elle atteindre le sol ? g= 9,8N/kg.
corrigé
énergie mécanique = énergie cinétique + énergie potentielle de pesanteur

EM= ½mv²+mgh = m(½v²+gh) = 0,03(0,5*3²+9,8*1,4)= 0,5446 ( 0,55 J)

Lorsque la hauteur maximale est atteinte, l'énergie mécanique est sous forme potentielle de pesanteur ; de plus l'énergie mécanique se conserve d'où :

EM= mghmax ; hmax =EM/(mg) = 0,5446/(0,03*9,8)=1,86 m

La bille repasse à l'altitude h=1,4 m avec la même vitesse v = 3 m/s.

écrire le théorème de l'énergie cinétique entre chaque passage à l'altitude h=1,4 m ( montée et descente) : le poids ne travaille pas , les altitudes de départ et d'arrivée sont identiques. ½mv²-½mv1²=0 d'où v=v1.

vitesse au sol lors de la descente : au sol l'énergie mécanique est sous forme cinétique ; l'énergie mécanique se conserve

½mv0² = EM soit v0² = 2EM/m =0,5446*2/0,03 = 36,3 ; v0 = 6,02 ( 6,0 m/s).
Mécanique

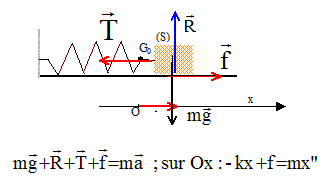
I- Déplacement d'une masse sur une surface rugueuse :

Un bloc de masse m est maintenu au point A contre un ressort comprimé, de constante de raideur k, sans lui être attaché. Le ressort est comprimé de DL. A t=0, le bloc glisse sur une surface horizontale rugueuse. Il parcourt une distance d, avant de s'immobiliser au point B.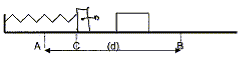

  1. Expliquer qualitativement les différentes phases du mouvement de ce bloc de masse m depuis le moment du lâcher jusqu'à l'arrêt. Justifier.
  2. Faire le schéma des forces exercées sur le bloc lorsque le bloc est au contact du ressort, lorsque le bloc n'est plus en contact du ressort.
  3. Donner l'expression de l'énergie mécanique en A et en B.
  4. La variation de cette énergie mécanique est égale au travail des forces de frottement f. Calculer la valeur de f supposée constante.
  5. Calculer la vitesse du bloc en C, au moment où il quitte le ressort.

DL= 20 cm ; k = 50 N/m ; m=0,2 kg ; longueur à vide du ressort L0 = 40 cm ; d = 0,5 m.

II- Cette fois on attache le bloc au ressort. On déplace le bloc au point A, en comprimant le ressort. A t=0 on lâche le système {masse + ressort }. La surface horizontale sur laquelle glisse le bloc est identique à celle de la question préédente.

  1. Faire l'inventaire des forces appliquées au système à une date t.
  2. Etablir l'équation différentielle du mouvement.
  3. Quelle est la nature du mouvement de cet oscillateur ?
corrigé
les différentes phases du mouvement : mouvement rectiligne

bloc contre le ressort : accéléré ( accélération non constante) ;

bloc séparé du ressort : uniformément freiné puis arrêt.

expression de l'énergie mécanique en A et en B :

en A l'énergie mécanique est sous forme potentielle élastique EA= ½kDL².

en B l'énergie mécanique est nulle EB=0

valeur de f supposée constante : EB-EA= - ½kDL² = Wf A-->B = -f AB = -fd

f = kDL² / (2d) = 50*0,2²/(2*0,5) = 2 N.

vitesse du bloc en C : énergie mécanique en C : EC= ½mv²

travail des frottements entre A et C : Wf A-->C = -f AC = -f (L0-DL)

diminution de l'énergie mécanique entre A et C = travail des frottements : ½mv²- ½kDL² = -f (L0-DL)

½mv² = ½kDL²-f (L0-DL) = 25*0,2² -2(0,4-0,2) = 1-0,4 = 0,6 J ; v² = 1,2/0,2 =6 ; v = 2,4 m/s.

inventaire des forces appliquées au système à une date t :

écrire la seconde loi de Newton sur l'axe Ox ( O position d'équilibre, ressort non déformé ):

équation différentielle du mouvement : -kx+f = mx" soit mx"+kx = f

nature du mouvement : rectiligne, périodique, amorti.
retour -menu