Aurélie 05/06

Radium, Uranium 235, Radon 211, Bore

d'après concours manipulateur électroradiologie médicale AP Paris

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Radium ( 4 pts)

Le curie est défini comme l'activité d'un gramme de radium ( 1 Ci = 3,7 1010 Bq). Le radium fut découvert en 1898. 22688Ra est émetteur a, sa période radioactive est de 1620 ans.

  1. Quelle serait en 2002, exprimée en Bq, l'activité d'un gramme de radium dont l'activité en 1898 était de 1 Ci ? Faire apparaître la résolution littérale.
  2. Pourquoi le becquerel a-t-il été préférée au curie dans le système SI.
  3. Que signifie "22688Ra est émetteur a " ?
  4. Ecrire l'équation de cette désintégration.
  5. Calculer en u la masse théorique du noyau de 22688Ra.
  6. La masse réelle du noyau de 22688Ra est 225,9771 u. Pourquoi la masse réelle est-elle différente de la masse théorique ?
  7. La masse réelle du noyau de 22286Rn est de 221,9703 u, la masse du noyau d'hélium est de 4,0015 u. Calculer en J et en MeV l'énergie libérée lors de la désintégration a d'un noyau de radium 226.
    masse : mp = 1,672 6231 10-27 kg ; mn =1,674 9286 10-27 kg ; 1 u = 1,660 5402 10-27 kg ; 1 eV= 1,602 10-19 J ; c= 3 105 km/s.
corrigé
activité actuelle d'un gramme de radium dont l'activité en 1898 était de 1 Ci :

A=A0 exp(-lt) ; l = ln2/t½ = ln2/(1620)=4,28 10-4 an-1 ; t = 2002-1898=104 ans

A=A0 exp(-ln2 t //t½)=A0 2( -t //t½) =A0 2(-104/1620) =0,956 A0 = 0,956 Ci ou 3,54 1010 Bq.

le becquerel a été préféré au curie car le curie est une unité bien trop grande.

signification de : "22688Ra est émetteur a " : lors de sa désintégration le radium 226 donne un noyau fils et un noyau d'hélium

22688Ra ---> AZX+ 42He

lois de conservation : conservation de la charge : 88 = Z+2 soit x=86 ( élément radon Rn)

conservation du nombre de nucléons : 226=A+4+y soit A=222

masse théorique du noyau de 22688Ra : 88 protons et 226-88 = 138 neutrons.

m= (88*1,672 6231 + 138*1,674 9286 )10-27 = 378,533 8636 10-27 kg

puis diviser par 1,660 5402 10-27 kg pour obtenir la masse en u : 227,958 3 u

masse réelle différente de la masse théorique :

La différence entre masse théorique et masse réelle correspond à l'énergie de liaison du noyau : un noyau est d'autant plus stable que son énergie de liaison par nucléon est grande.

énergie libérée par la réaction d'un noyau de radium 226 :

Dm= m(22286Rn) + m(42He) - (22688Ra) =221,9703 + 4,0015 - 225,9771 = -0,0053 u

puis -0,0053 *1,66 10-27 = 8,8 10-30 kg

E= |Dm|c² = 8,8 10-30 *(3108)² =7,9 10-13 J ou 7,9 10-13 /1,6 10-19 = 4,9 106 eV= 4,9 MeV


fission( 4 pts)

Dans une centrale nucléaire, une des réactions possibles est représentée par : 23592U+ 10n---> 9438Sr+ 139xXe+y 10n

  1. Calculer les valeurs de x et y en justifiant.
  2. Calculer en eV l'énergie libérée au cours de cette réaction.
  3. L'uranium 235 est radioactif de type a. Le noyau fils obtenu est le Thorium. Ecrire l'équation de cette désintégration.
  4. La demi-vie de l'uranium 235 vaut t½= 4,5 109 ans. Quelle est l'activité de 1,0 g d'uranium 235 ? Préciser l'unité SI.
    masse en u : m(23592U) = 235,0134 ; m(9438Sr) =93,8946 ; m(139xXe) = 138,8882 ; m(neutron) = 1,0087
    1 u =1,67 10-27 kg ; NA= 6,02 1023 mol-1 .
corrigé
23592U+ 10n---> 9438Sr+ 139xXe+y 10n

lois de conservation : conservation de la charge : 92 = x+38 soit x=54

conservation du nombre de nucléons : 235+1=94+139+y soit y=3

énergie libérée par la réaction d'un atome d'uranium 235 :

Dm= m(9438Sr) + m(139xXe) + 3 m(neutron) -m(23592U) = 93,8946 + 138,8882 +2*1,0087- 235,0134 = -0,2132 u

puis -0,2132 *1,66 10-27 = 3,54 10-28 kg

E= |Dm|c² = 3,54 10-28*(3108)² =3,185 10-11 J ou 3,185 10-11 /1,6 10-19 = 1,99 108 eV= 199 MeV

 activité de 1,0 g d'uranium 235 : A= l N

N= masse / masse molaire * NA= 1/235*6,02 1023 =2,56 1021 noyaux d'uranium 235 dans 1 g.

lt½=ln2 soit l =ln2 / t½=ln2 / (4,5 109*365*24*3600) =4,88 10-18 s-1.

A= l N = 4,88 10-18 *2,56 1021=1,25 104 Bq.

Radon 211( 3,5 pts)

L'isotope radon 211 ( 21186Rn) se désintègre par radioactivité a en émettant une particule a et en donnant un noyau de Polonium

  1. Ecrire les lois de conservation vérifiées au cours de cette désintégration. En déduire l'équation bilan de cette désintégration.
  2. Exprimer en MeV puis en joules l'énergie libérée par la désintégration d'un atome de radon.
    On effectue une analyse cinétique des particules émises. L'expérience montre que l'énergie cinétique totale peut prendre trois valeurs différentes : 5,96 MeV ; 5,89 MeV ; 5,72 MeV
  3. Comment interptéter ces résultats ?
    En déduire le nombre d'états excités du polonium et le nombre de raies d'émission que l'on peut observe, ainsi que les énergies des photons émis.
    masse en u : m(radon) = 210,9906 ; m(polonium) =206,9816 ; m(hélium) = 4,0026.
    1 u correspond à 931,5 MeV/c².
corrigé
21186Rn--->AZPo +42He

lois de conservation : conservation de la charge : 86 = Z+2 soit Z=84

conservation du nombre de nucléons : 211=A+4 soit A= 207

énergie libérée par la désintégration d'un atome de radon :

Dm= m(polonium) + m(hélium) - m(radon) = 206,9816 + 4,0026 - 210,9906 = -0,0064 u

puis 0,0064*931,5 = 5,96 MeV ou 5,96 106*1,6 10-19 = 9,54 10-13 J.

L'énergie cinétique totale peut prendre trois valeurs différentes : le noyau fils se trouve dans différents états excités ; le retour à l'état fondamental ou à un état de moindre énergie, s'accompagne de l'émission de photons.

L'état fondamental de moindre énergie correspond à 5,72 MeV ; les deux états excités correspondent à 5,89 et 5,96 MeV

énergies des photons émis : 5,89-5,72 =0,17 MeV ; 5,96-5,89 = 0,07 MeV ; 5,96-5,72 = 0,24 MeV.

On observe 3 raies d'émissions.

Source de Césium 137 (6 pts)

 On utilise en curiethérapie le césium 137 dans le traitement in situ du cancer de l'utérus. Le traitement consiste à soumettre une patiente à un échantillon de césium 137 ( 13755Cs) pendant quelques jours. La constante de radioactivité l de ces noyaux est 7,3 10-10 s-1. L'activité A0 d'un échantillon de cet isotope est 3,0 105 Bq.

Le césium 137 est un émetteur b- et g. (Numéro atomique 54 pour Xe et 56 pour Ba.

  1. Expliquer la phrase " Le césium 137 est un émetteur b- et g".
  2. Ecrire l'équation de désintégration du césium 137 en précisant les règles de conservation utilisées.
  3. Donner la définition du temps de demi vie t½.
  4. Donner l'expression de l'activité A(t) à un instant t, en fonction de A0, du temps t et de la consatnte radioactive l.
  5. Etablir l'expression entre la constante radioactive et le temps de demi-vie. Calculer t½.
  6. Construire la courbe donnant l'activité A(t) en fonction du temps, en précisant quelques points particuliers.
  7. Comment évolue l'activité durant le traitement ?
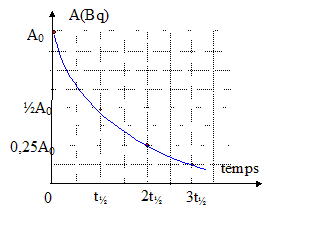
corrigé
Le césium 137 est un émetteur b- et g" :

le césium 137 instable se désintègre en émettant un électron et un noyau fils excité ; ce dernier revient à un état de moindre énergie en émettant des photons g.

équation de désintégration du césium 137 :

13755Cs --->AZX* + 0-1 ; AZX* ---> AZX +00g

lois de conservation : conservation de la charge : 55 = Z-1 soit Z=56 (élément baryum Ba)

conservation du nombre de nucléons : 137=A+0 soit A=137

définition du temps de demi vie t½. :

durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.

expression de l'activité A(t) =A0 exp(-lt)

expression entre la constante radioactive et le temps de demi-vie :

A(t½) =½A0 = A0 exp(-lt½) ; ½ = exp(-lt½) ; ln2 = lt½

t½ = ln 2 / l = ln2 / 7,3 10-10 = 9,5 108 s = 30 ans

courbe donnant l'activité A(t) en fonction du temps :

l'activité durant le traitement reste pratiquement constante car le traitement ne dure que quelques jours, valeur très inférieure à la demi vie ( 30 ans).

retour -menu