|
d'après bts travaux publics 2006 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
Une cuve remplie de 300 L de propane C3H8 liquide sous haute pression sert à alimenter le brûleur d'une chaudière. La masse volumique du propane liquide à la température de la cuve est rliq= 508 kg m-3.
Données : O : 16 g/mol ; capacité thermique massique de l'eau : c=4180 J kg-1 K-1. corrigé Masse en kg de propane dans la cuve : volume (m3) fois masse volumique du propane ( kg m-3) = 0,3*508 = 152,4 kg. Masse molaire du propane : M= 3*12+8 = 44 g/mol. Quantité de matière (mol) de propane dans la cuve : masse (g) / masse molaire (g/mol) = 152400/44 = 3463,6 mol. Volume de propane sous forme gazeuse pouvant être libéré par la cuve : Le volume molaire des gaz est Vm=24 L/mol volume (litre ) = quantité de matière (mol) * volume molaire (L/mol) = 3463,6*24 =8,31 104 L = 83,1m3.
Equation de la réaction de combustion du propane : C3H8 + 5O2 ---> 3CO2+4H2O ( gaz) Volumes de vapeur d'eau Veau et de dioxyde de carbone, VCO2 libérés par cette combustion : n(H2O) = 4 n(C3H8 ) soit Veau = 4 volume de propane = 4*83,1 =333 m3. n(CO2) = 3 n(C3H8 ) soit VCO2 = 3 volume de propane = 3*83,1 =249 m3. énergie Q disponible : Le pouvoir calorifique supérieur noté PCS du propane est tel que PCS= 49,6 MJ / kg. Q= 49,6 * 152,4 = 7,56 103 MJ = 7,56 109 J. Cette chaudière sert à chauffer de l'eau provenant de
six radiateurs. Le débit massique qm de l'eau
dans les radiateurs et tel que : qm= 0,035 kg/s.
La température d'entrée dans le radiateur est 75°C et celle de sortie
de 60°C. Q1 = mCDt avec C = 4180 J kg-1 K-1 ; Dt = 75-60 = 15 °C et m : masse d'eau débitée en 3600 s par un radiateur soit m = 0,035*3600 / 6 = 21 kg Q1 = 21*4180*15 =1,32 106
J. Chaleur Q3 fournie par la chaudière en 1 heure ainsi que la puissance de celle-ci : Le rendement de la chaudière est de 79,6%. Q3= Q2 /0,796 = 9,92 106 J ; puissance (W) = énergie (J) / durée (s) ; P= Q3/ 3600 = 2,75 kW. Débit massique du gaz arrivant à la chaudière : Puissance (kW) = débit masique ( kg/s) * PCS( kJ/kg) débit masique ( kg/s) = 2,75 / 49,6 103 = 5,6 10-5 kg/s.
|
|
|
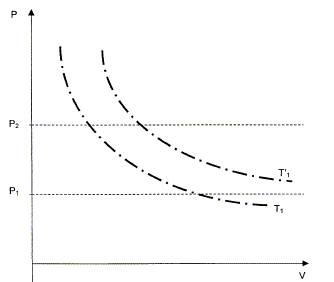
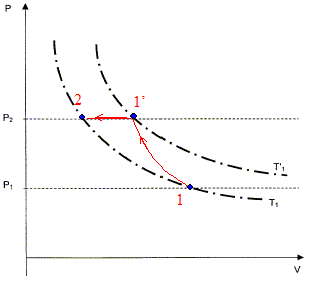
On veut comprimer une mole de gaz supposé parfait de l'étatinitial noté 1 caractérisé par (V1, P1= 105 Pa, T1=298 K ) vers un état final noté 2 caractérisé par (V2, P2= 2 105 Pa, T2). Cette compression est réalisée en deux étapes : - Une compression adiabatique qui amène le gaz dans un état intermédiaire noté 1' caractérisé par (V'1, P2, T'1 ). - Un refroidissement isobare pour obtenir l'état 2 caractérisé par (V2, P2= 2 105 Pa, T1).
Données : R= 8,31 J K-1 mol-1 ; g= 1,4 ; Cp, m = gR / (g-1), capacité calorifique molaire à pression constante. corrigé 
Calcul de V1 : V1 = RT1/P1 =8,31*298/105 =2,48 10-2 m3 =24,8 L / mol.
calcul de V'1 et T'1 : transformation adiabatique : P1V1g = P2V'1g ; V'1g = P1/ P2 V1g ; V'1 = ( P1/ P2 ) 1/g V1 V'1 =(0,5)1/1,4 24,8 = 15,1 L/mol. équation des gaz parfaits : T'1 = V'1 P2 /R = 15,1 10-3*2 105 /8,31= 364 K. On veut mesurer les travaux reçus W1, W2 et Wt correspondant successivement à la transformation adiabatique, le refroidissement isobare et à la transformation totale. Calcul de W1 en utilisant la relation W1 = R(T'1-T1)/ ( g-1) W1 = 8,31(364-298) / 0,4 =1,37 kJ. transformation isobare : dW2 = -P2dV ; W2 = -P2( V2 - V'1 ); or P2V2 = RT2= RT1 et P2V'1 = RT'1 d'où W2 = R( T'1-T1) W2 = 8,31(364-298) = 0,55 kJ. Wt = W1 + W2 = 1,92 kJ. On veut maintenant mesurer les échanges de chaleur Q1, Q2 et Qt Q1 = 0 car la compression est adiabatique. Q2 = Cp, m ( T1-T'1) = gR / (g-1)( T1-T'1)=1,4*8,31/0,4(298-364) = -1,92 kJ. Qt = Q2 = -1,92 kJ. Variation d'énegie interne DU = Wt + Qt = 0 La variation d'énergie interne d'un gaz parfait ne dépend que de la température finale et de la température initiale. Or ici la température initiale est égale à la température finale, d'où DU =0.
|
||
|
Deux sources S1 et S2 omnidirectionnelles sont placées côte à côte.
Données : Li= Lw-11-20 log r où r représente la distance du point à la source. I0 = 10-12 W m-2. corrigé Intensité sonore I perçue au point A lorsque les deux sources fonctionnent simultanément : Li = 80 dB. Li = 10 log(I/I0) soit I = I0 100,1L = 10-12*108 = 10-4 W m-2. Niveau de puissance Lw global imposé par ces deux sources : Li= Lw-11-20 log r avec Li = 80 dB et r = 5 m Lw = Li + 11 + 20 log r = 80+11+20 log 5 = 105 dB. Intensité sonore I2 percu au point A lorsque S2 fonctionne seule : Lorsque la source S1 fonctionne seule, le niveau d'intensité en ce point A est Li1 = 75 dB. Intensité sonore I1 perçue au point A lorsque S1 fonctionne seule : I1 = I0 100,1L = 10-12*107,5 = 10-4,5 = 3,16 10-5 W m-2. I1 + I2 =I soit I2 = I-I1 = 10-4 - 3,16 10-5 =6,84 10-5 W m-2. Niveau d'intensité Li1 lorsque S2 fonctionne seule : Li1 = 10 log(I2/I0)
= 10 log (6,84 10-5 /
10-12)= 78,3
dB.
Niveau d'intensité sonore Li' en ce point lorsque les deux sources fonctionnent simultanément : Lw = L'i + 11 + 20 log r =105 dB avec r= 10 m L'i = 105-11-20log 10 = 105-31 = 74 dB. Intensité sonore I' perçue en B : I' = I0 100,1L' = 10-12*107,4 = 10-4,6 = 2,5 10-5W m-2.
|
||
|
|