|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||
| .
. |
||
|
||
|
|
L'ammoniac utilisé comme fluide frigorigène a pour formule NH3.
Données : Couples acide-base : NH4+/NH3 ; H2O/HO- ; Produit ionique de l'eau à 25°C : Ke =1,0 10-14. corrigé composition de chaque noyau : azote : 7 protons et 14-7 = 7 neutrons ; hydrogène : 1 proton structure électronique de chaque atome : azote : 7 électrons soit 2 sur le premier niveau et 5 sur le second niveau d'où K2 L5. hydrogène : un seul électron d'où K1. L'atome d'azote a tendance à compléter à 8 sa couche électronique externe en mettant en oeuvre 3 liaisons de covalence simple. L'atome d'hydrogène a tendance à compléter à 2 sa couche électronique externe en mettant en oeuvre une liaison de covalence simple. équation de la réaction de l'ammoniac avec l'eau : NH3 + H2O = NH4++ HO-. [H3O+] = 10-pH = 10-10,6 = 2,5 10-11 mol/L ; [HO-]= Ke/[H3O+] = 10-14 /2,5 10-11 = 4 10-4 mol/L concentration de la solution d'ammoniac : à l'équivalence du dosage les quantités de matière d'acide et d'ammoniac sont en proportions stoechiométriques soit : 0,015*13,3 = 20 c ; c = 0,015*13,3/20 = 0,01 mol/L
|
|
|
Celle-ci comprend principalement quatre éléments : un compresseur C, un condenseur, un détendeur D, un évaporateur.  Le cycle est supposé réversible. Le fluide frigorigène utilisé est l'ammoniac (R 717). Il est considéré comme un gaz parfait à l'état gazeux. Données : g=1,30
; relations de Laplace pour un gaz parfait lors d'une transformation
adiabatique PVg=Cte
; TVg-1=Cte
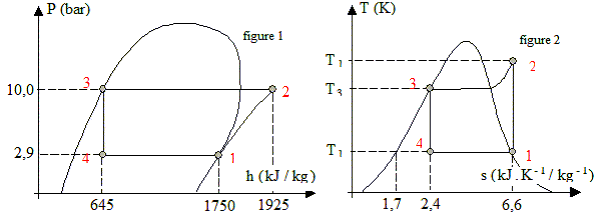
; P1-gTg=Cte Description du cycle : Le fluide sort de l'évaporateur sous forme de vapeur saturante sèche à l'état 1 : pression P1 = 2,90 bar , température T1=263 K . Il subit dans le compresseur, une compression adiabatique réversible qui l'amène à l'état 2 : pression P2 = 10,0 bar, température T2 . La vapeur subit dans le condenseur une transformation à pression constante : refroidissement jusqu'à la température, puis liquéfaction totale à cette température (état 3). Le liquide passe dans le détendeur et y subit une détente isenthalpique qui le ramène à la pression initiale P1 = P4=2,90 bar et à la température T4=263 K (état 4). La vaporisation du liquide restant se termine dans l'évaporateur pour un retour à l'état 1.
Les graphes des figures 1 et 2 ne sont pas à l'échelle. On n'a fait figurer que des repères indiquant les coordonnées des points. 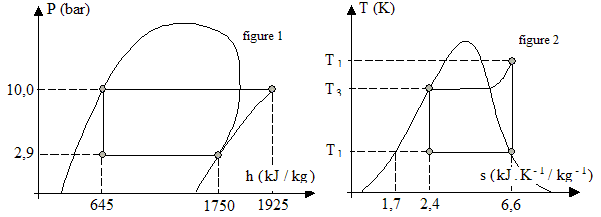
T2 =[P1/P2]1/g-1T1 avec 1/g-1 = 1/1,3-1 = -0,23 ;T2 = 0,29-0,23*263= 350 K quantité de chaleur Q23 échangée par kilogramme de fluide dans le condenseur : la transformation étant isobare, Q23 est égale à la variation de l'enthalpie massique c'est à dire : pour le fluide à l'état gazeux évoluant de T2 à T3 : cp(T3-T2) =2,12(298-350)= -110 kJ kg-1. lors du changement d'état physique à température constante : -Lv3 = -1170 kJ kg-1. Q23 =cp(T3-T2)--Lv3 = -110-1170 = -1280 kJ kg-1. cette valeur étant négative, la chaleur est cédée au milieu extérieur, dont la température est inférieure à 298 K. sens de l'échange dans l'évaporateur : Q41 positif, donc le fluide reçoit de l'énergie de la part du milieu extérieur dont la température est supérieure à la température T4 du fluide ( écoulement de la chaleur du corps le plus chaud vers le corps le plus froid) travail W échangé par kilogramme de fluide avec le milieu extérieur au cours du cycle : appliquer le premier principe à 1 kg du fluide sur un cycle : W+Q12 +Q23 + Q34 +Q41=0 Q12 =0 , compression adiabatique ; Q34 =0 détente rapide, très peu d'échange avec l'extérieur soit W=-Q23 -Q41 =1280-1105=175 kJ kg-1. efficacité , rapport du gain sur l'énergie dépensée =Q41 /W= 1105/175 = 6,3.
A partir du diagramme approprié, calcul les valeurs des quantités de chaleur Q23, Q41 et du travail W échangé : Dans l'évaporteur, transformation isobare, la chaleur reçue par le fluide est égale à la variation d'enthalpie : Q41 = h1-h4 = 1750-645=1105 kJ/kg Même raisonnement dans le condenseur : Q23 = h3-h2 = 645 - 1925= -1280 kJ/kg écrire le premier principe ; W+Q= Dh avec W : travail fourni par les parties mobiles de la machine ( situées uniquement dans le compreesuer) - compresseur ( Q12=0 adiabatique) d'où W= h2-h1 =1925-1750 = 175 kJ/kg |
||
|
La plaque signalétique du moteur asynchrone entraînant le compresseur porte les indications suivantes : 400 V / 690 V ; 2,6 kW ; cos j=0,79 ; 50 Hz ; 6A / 3,5 A ; 940 tr/min Ce moteur est étudié en régime de fonctionnement nominal.
corrigé tension nominale aux bornes d'un enroulement du stator : 400 V couplage les enroulements du stator : dans le couplage étoile, la tension aux bornes de chaque enroulement est égal à la tension simple 400 V alors que dans un couplage triangle, la tension aux bornes de chaque bobine serait 690 V; ce qui n'est pas prévu par le constructeur. intensité efficace du courant traversant un enroulement : dans le couplage étoile, l'intensité efficace dans chaque enroulement est égale à l'intensité en ligne soit 6,0 A. vitesse de synchronisme de ce moteur : ns= vitesse de rotation (tr/s) / nombre de paires de pôles avec f = 50 Hz ns =50 /p tr/s ou 50*60 / p = 3000 / p tr/min Or la vitesse de rotation du moteur ( 940 tr/min) est très proche de la vitesse de synchronisme : d'où ns= 1000 tr/min et p = 3. glissement g = (ns-n)/ns = (1000-940)/1000 = 0,06 ( 6%). puissance absorbée par ce moteur : Pabs= 3½U Icosj =3½*400*6*0,79 = 3,28 kW. puissance transmise au rotor : Ptr = Pabs-Pfs- PJs=3280-200-190 = 2,89 kW. moment du couple électromagnétique : puissance électromagnétique Pém = (1-g)Ptr = 0,94*2,89 = 2,72 kW moment du couple T= Pém /(2pn) avec n =940/60=15,67 tr/s ; T= 2720/(6,28*15,67)=27,6 N m. pertes par effet Joule au rotor : g Ptr = 0,06*2890 =173 W pertes mécaniques : Pm= Pem - Putile (Putile est indiquée sur la plaque signalétique du constructeur) Pm=2720-2600=120 W rendement de ce moteur : Putile /Pabs=2,6/3,28 = 0,79 ou 79% couple utile de ce moteur : Putile / (2pn) avec n =940/60=15,67 tr/s ; T= 2600/(6,28*15,67)=26,4 N m.
|
||
|
|