|
d'après bts domotique 2006 En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
|
Le moteur de Stirling fait aujourd'hui l'objet de nombreux programmes de recherche développement aux États-Unis, au Japon et en Europe du Nord, où il y a déjà quelques opérations de démonstration en vraie grandeur, notamment en Allemagne et aux Pays-Bas. Le moteur de Stirling présente des avantages significatifs par rapport à un moteur à explosion, Diesel ou essence : · peu de maintenance et une longue durée de vie ; · moteur peu bruyant ; · la combustion extérieure et continue, à basse pression, peut être parfaitement contrôlée pour émettre peu de gaz polluants (3 à 4 ppm d’oxydes d’azote) ; · enfin, dans les installations de cogénération, la quasi-totalité de la chaleur non dépensée peut être récupérée et exploitée, ce qui conduit à un rendement global potentiel très élevé, de l'ordre de 95 %. Les températures notées T sont des températures absolues, en K. Généralités sur les moteurs Un moteur est un système fermé échangeant un travail W avec l’extérieur, une chaleur QF avec une source froide (température TF) et une chaleur QC avec une source chaude (température TC).
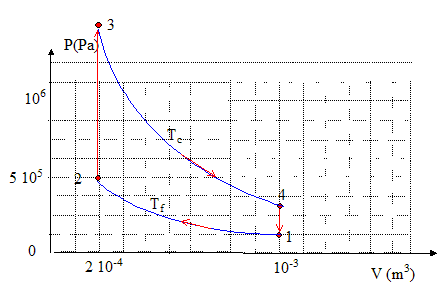
travail cédé à l'extérieur, négatif par définition Qc recu par le système, positif par définition Qf cédée par le système, négatif par définition rendement : travail mis en jeu / Chaleur cédée par la source chaude rendement Carnot : (Tc-Tf)/Tc. Il n'existe pas, à priori, un moteur de plus grande performance, à TF et TC données : dans le cycle de Carnot, toutes les transformations sont réversibles et le rendement est maximum. allure du cycle de transformations relatif à ce moteur en coordonnées de Clapeyron (P, V),
nombre de moles de gaz parfait mis en jeu : avec les données de l'état 1 par exemple n= PV/RT = 105*10-3
/ (8,31*270)= 4,46 10-2
mol. Lors de la transformation 1-->2, le travail W12 reçu par la quantité n de gaz parfait s'écrit : P= nRT/ V d'où : dW= -nRT/ VdV = -nRTf d ln V à Tf = constante. puis intégrer entre V1 et V2 d'où W12=nRTfln(V1/V2) de plus à température constante V1/V2= P2/P1 d'où : W12=nRTfln(V1/V2) = nRTfln(P2/P1) Travaux W12, W23, W34, W43 échangés au cours des différentes transformations du gaz, ainsi que le travail total échangé au cours du cycle : W12 = 4,46 10-2 *8,31*270 ln (10-3 / 2 10-4) = 161 J. W23=0 ( isochore) ; W41 = 0 ( isochore) W34= nRTc ln( V3/V4) = 4,46 10-2 *8,31*770 ln (2 10-4/10-3 ) = -460 J. W= -460+161 = -299 J. variations d'énergie interne : DU12 = DU34 = 0 ( isothermes) quantités de chaleur Q12 et Q34 : en conséquence W34+Q34=0
soit Q34 = - W34 = 460 J
; W12+Q12=0
soit Q12 = - W12 = -161 J rendement =| (W12+W34)/ Q34 |= | (W12+W34)/ (-W34 ) |=| -W12/W34-1| W12 / W34= -Tf / Tc d'où le rendement : |Tf / Tc -1| = |270 / 770-1 |= 0,65. rendement intèressant car identique au rendement d'une machine de Carnot fonctionnant entre deux source de chaleur aux même températures que ce moteur. Le cycle est répété 500 fois par minute, la puissance mécanique fournie par le moteur à l'alternateur vaut : travail total sur un cycle : 299 J sur 500 cycles : 299*500 = 1,5 105 J puissance 1,5 105 /60 = 2,5 kW. puissance thermique fournie au système de chauffage de la maison : 161*500/60 = 1,3 kW.
|
|||||||||||||||||||||||||||||||||||
|
Un moteur est situé dans un local de surface au sol 2*2,5 m² et de hauteur 2,5 m. Toutes les parois de ce local sont en béton ( coefficient d'absorption a1 = 0,02) On mesure , quand ce moteur fonctionne, le niveau d'intensité acoustique Lp à l'aide d'un sonomètre équipé d'un analyseur de filtres d'octaves de fréquences centrales f0.
Formule de Sabine pour la durée dr réverbération d'un local : T= a(V/A) avec a = 0,16 s m-1 ; V : volume du local ; A : aire absorbante équivalente. Variation DL du niveau acoustique résultant d'une variation de la durée de réverbération DL= 10 log (T2/T1) corrigé niveau de pression acoustique total noté L1 : pour chaque intervalle, calcul du niveau d'intensité acoustique I= I0 100,1 L = 10-12 * 100,1 L :
L1 = 10 log (Itotal
/ I0 ) = 10 log (2,68 10-6
/ 10-12) = 64,3
dB.
Formule de Sabine pour la durée dr réverbération d'un local : T= a(V/A) avec a = 0,16 s m-1 ; V : volume du local ; A : aire absorbante équivalente. A= aire totale du local *coefficient d'absorption a1 du béton aire du local = aire sol + aire plafond + aire des murs = 5 +5 + 9*2,5 =32,5 m² A= 32,5a1 = 32,5*0,02 =0,65 m² volume du local : V= 5*2,5 = 12,5 m3. T1 = 0,16 *12,5/0,65 =3,1 s.
durée de réverbération notée T2 : A= aire absorbante équivalente = aire du plafond a2 + aire des murs a1 A = 5*0,8 + 27,5*0,02 =4,55 m². T2 = 0,16 *12,5/4,55 =0,44 s. nouvelle valeur du niveau de pression acoustique total noté L2: Variation DL du niveau acoustique résultant d'une variation de la durée de réverbération DL= 10 log (T2/T1) DL= 10 log (0,44/3,1) = -8,5 dB ; L2 = 64,3-8,5 = 55,8 dB.
|
||||||||||||||||||||||||||||||||||||
|
On souhaite dissoudre le calcaire ou carbonate de calcium CaCO3 existant dans une canalisation. Pour cela on utilise l'acide chlorhydrique du commerce. L'équation de la réaction est : Ca2+ + CO32- + 2(H+ + Cl-) = CO2 + H2O+ Ca2+ +2Cl-
Ca : 40 ; C : 12 ; O : 16 g/mol H3O+/H2 : V ; Fe2+/Fe : -0,44 V ; Cu2+/Cu : 0,34 V ; Pb2+/Pb : -0,13 V. corrigé masse de carbonate de calcium dissoute avec 1L de solution d'acide chlorhydrique de concentration C= 11 mol/L : quantité de matière d'acide (mol) = volume (L) * concentration (mol/L) =1*11 = 11 mol Ca2+ + CO32- + 2(H+ + Cl-) = CO2 + H2O+ Ca2+ +2Cl- D'après les coefficients de l'équation, la quantité de matière de carbonate de calcium est égale à la moitié de la quantité de matière d'acide soit 5,5 mol. Masse molaire CaCO3 : M= 40 +12+3*16 = 100 g/mol masse (g) = masse molaire (g/mol) * quantité de matière
(mol) = 100 *5,5 = 550 g.
Le facteur de dilution est égal à : F= 500/5 = 100 ; la solution diluée est 100 fois moins concentrée que la solution commerciale. pH = 1= - logc d'où c = 0,1 mol/L et C= 100*0,1 = 10 mol/L.
L'indicateur coloré change de couleur à l'équivalence ( passage du jaune au bleu). L'indicateur coloré permet de repèrer l'équivalence. La solution titrante est une solution d'hydroxyde de sodium de concentration cb=0,10 mol/L. Le volume de solution titrante nécessaire pour atteindre l'équivalence est 10,8 mL : à l'équivalence caVa = cbVb soit ca= cbVb / Va =0,1*10,8/10 = 0,108 mol/L et C= 100*0,108 = 10,8 mol/L L'indication portée par l'étiquette est correcte ( écart
relatif =(11-10,8)/10,8 *100 = 2 % )
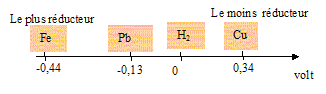
Il est possible d'utiliser l'acide chlorhydrique pour détartrer une canalisation de cuivre (H3O+ n'attaque pas le cuivre) ; par contre le plomb et le fer ( fonte) sont des métaux plus réducteurs que H3O+ : en conséquence le plomb et le fer sont attaqués par H3O+ ; le détartrage par l'acide chlorhydrique n'est pas possible dans ce cas.
|
||||||||||||||||||||||||||||||||||||
|
|