|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||
|
|||||||||||||||||
|
|
Les questions 4 et 5 de l'exercice sont indépendantes des autres questions. En sortant de cours, un élève de terminale, violoniste amateur depuis quelques années, examine son instrument de musique pour en comprendre le fonctionnement. Le violon possède quatre cordes, que l'on frotte avec un archet.  La nature et la tension des cordes sont telles qu'en vibrant sur toute leur longueur (AO = l = 55,0 cm), elles émettent des notes dont les caractéristiques sont données ci-dessous :
Une onde progressive se propage le long d'une corde tendue entre deux points fixes à la célérité v =(F/m)½ avec F la tension de la corde et µ sa masse linéique. Chaque corde du violon a une tension et une masse linéique qui lui sont propres. On admet qu'un diapason émet un son de fréquence unique 440 Hz.
La déformtion de la corde est perpendiculaire à la direction de propagation de l'onde. La longueur l de la corde vibrante est liée à la longueur d'onde l par la relation : l = ½l Si la longueur de la corde est un multiple de la demi-longueur d'onde, alors une onde stationnaire apparaît sur la corde :l = ½ nl si n=
1 on observe un seul fuseau. ( mode
fondamental) Tension de la corde après cette opération ( l'élève accorde son violon) µ= 0,95 g.m-1 = 9,5 10-4 kg m-1 ; f = 440 Hz ; v =(F/m)½ ; l = 55,0 cm longueur d'onde : l = 2l =1,10 m ; célérité v =l * f = 1,10*440 = 484 m/s F/m
= v² ; F= v² m
=4842*9,5 10-4 =2,2 102N.
en conséquence, la longueur d'onde est
modifiée, ainsi que la fréquence. fréquence du fondamental f (la3) =440 Hz ; v = 484 m/s ( tension et masse linéique inchangées) ; or v= l f et l = 2l soit v= 2l f ( pur le mode fondamental) 2l(la3) f(la3) = 2l(ré3) f(ré3) ; l(la3) = l(ré3) f(ré3) / l(ré3) l(la3) = 0,55*294/ 440 = 0,37 m, distance ceevalet - point
d'appui.
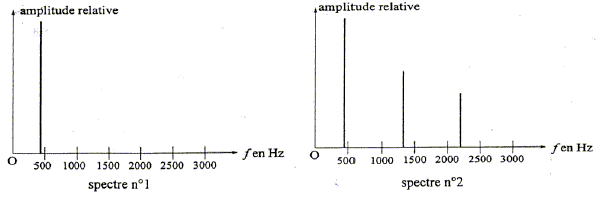
spectre 1 : un seul pic, il s'agit d'un son pur de fréquence f = 440 Hz, son émis par le diapason. spectre 2 : on distingue plusieurs harmoniques
; le son est complexe, son émis par le violon ( corde du la3). Les fréquences des harmoniques sont des multiples de la fréquence du mode fondamental : 880 Hz ( n=2 ) ; 1760 Hz ( n=4 ) et 2640 Hz (
n=6)
Or les intensités sonores s'additionnent d'où Itotal = 2I = 2 I0 100,1L Itotal /I0 = 2 100,1L ; log (Itotal /I0 ) = log 2 + 0,1 L 10 log (Itotal /I0 ) = 10 log 2 + L le niveau sonore augmente de 10 log 2 = 3 dB
soit 73 dB
lorsque l'élève et le violoniste joueront ensemble
f2 / f1 = 294/196 = 1,5 et f3 / f2 =440/294 = 1,5 soit fn+1 = 1,5 fn ; par suite la valeur de la fréquence f4 = 1,5 f3 = 1,5 *440 = 6,6 102 Hz.
|
||||||||||||||||
|
|
|||||||||||||||||
|
|