|
Le piège photo En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
|
|||
|
|
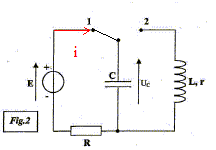
Cet exercice étudie le principe de fonctionnement d'un piège photo réalisé par un ornithologue afin d'identifier le prédateur d'une espèce d'oiseau en voie de disparition. Un œuf de caille posé sur un commutateur à bascule sert d'appât dans un vieux nid. Lorsque le prédateur prélève l'œuf, le commutateur bascule de la position 0 à la position 2. Le condensateur initialement chargé se décharge dans un électroaimant que l'on peut modéliser par une bobine d'inductance L et de résistance interne r. L'électroaimant, placé sur un appareil photo déclenche la prise de vue. Le circuit de charge est constitué d'un condensateur de capacité C, d'un conducteur ohmique de résistance R et d'un générateur idéal de tension de fem E= 8 V. 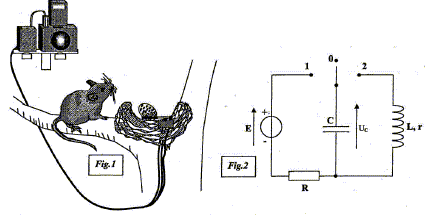 I- Armement du dispositif. Le dispositif s'arme en plaçant le commutateur en position 1 pendant la durée nécessaire à la charge du condensateur. Cette opération réalisé, l'œuf est déposé sur le bras du commutateur à bascule qui est ainsi maintenu en position O.
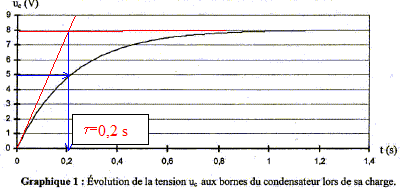
Déclenchement du piège Lorsque l'œuf est prélevé, le commutateur bascule de la position 0 à la position 2. Un enregistrement de la tension uc(t) aux bornes du condensateur est réalisé lors de l'étude de ce dispositif.
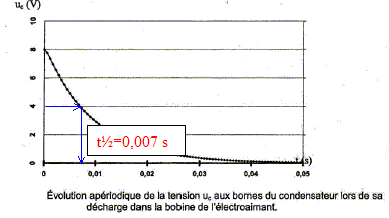
Détermination de l'inductance L de la bobine constituant l'électroaimant. On place cette bobine en série avec un condensateur de capacité C'= 10 nF initialement chargé sous une tension de 6V et une résistance R' tel que R'+r= 50 ohms. Le circuit ainsi constitué est représenté ci-dessous : 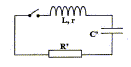 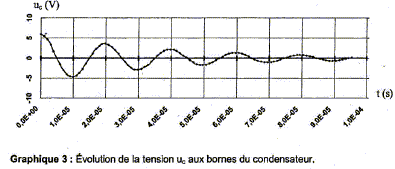 L'évolution de la tension aux bornes du condensateur a été enregistrée à la fermeture de l'interrupteur.
sens réel du courant i lors de la charge :
équation différentielle vérifiée par uc(t) lors de la charge : uc+Ri =E (1) (loi d'additivité des tensions) de plus i = dq/dt et q=Cuc soit i = Cduc/dt ; repport dans (1) d'où : uc+RCduc/dt = E On pose t = RC ; par suite : uc+t duc/dt = E analyse dimensionnelle : R résistance soit tension / intensité ; C capacité soit charge / tension d'où on déduit : RC charge / intensité or une charge est une intensité fois un temps ; par suite RC a la dimension d'un temps. valeur de uc(t) en régime permanent : en régime permanent uc(t) est constant : donc duc/dt = 0 ; uc+t duc/dt = E s'écrit : Uc=E. solution de l'équation différentielle : uc(t) = A(1-exp(-t/t)) ; dériver par raport au temps ; duc/dt = A/t exp(-t/t) repport dans l'équation différentielle : A(1-exp(-t/t)) + A exp(-t/t) = E A- A exp(-t/t)+ A exp(-t/t) = E uc(t) = A(1-exp(-t/t)) est solution de l'équation différentielle si A= E. tension aux bornes du condensateur à t=5t : uc(5t) = E(1-exp(-5t/t)) =E(1-exp(-5)) = 0,993 E à 0,7 % près on peut considérer que la charge du condensateur est terminée. valeur de t :
abscisse de l'intersection de la tangente à t=0 avec l'asymptote horizontale ou bien abscisse correspondant à uc= 0,63 E= 0,63*8 = 5 V. La charge du condensateur est pratiquement terminée à t = 5 t soit 1 s. Durée caractéristique : à t½ uc = ½E = 4 V
L'énergie initialement stockée dans le condensateur doit être la plus grande possible : E =½CE² en fin de charge Cette énergie sera d'autant plus grande que E sera plus grand et que la capacité C sera plus grande. 
Nom du régime correspondant au graphe ci-dessus : régime pseudo-périodique. Inductance de la bobine : pseudo-période T= 2,0 10-5 s (lecture graphe) de plus T= 2p(LC)½ ; T² = 4p² LC soit L= T²/(4p² C) avec C= 10-8F. L= 4 10-10/(4*3,14² 10-8)= 1,0 10-3 H.
|
||
|
|
|||
|
|