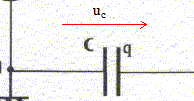Aurélie 6/3/06

d'après concours manipulateur électroradiologie médicale Toulouse 2005

étude d'un condensateur.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.



Etude d'un condensateur.

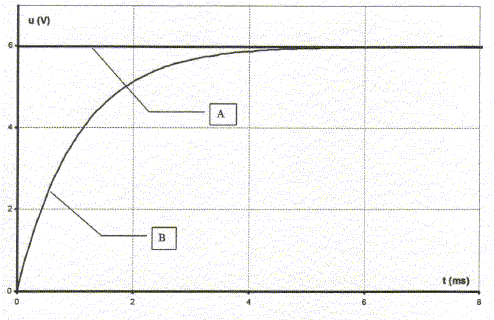
R= 500 W. Un oscilloscope à mémoire suit l'évolution temporelle des deux tensions. A la fermeture de l'interrupteur (t=0) le condensateur est initialement déchargé.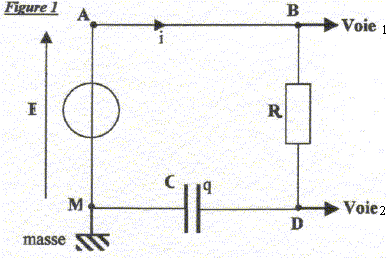

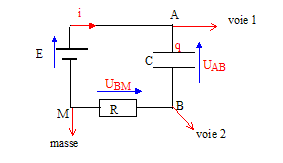
  1. Nommer les tensions mesurées sur chaque voie. Schématiser la tension aux bornes du condensateur ( convention récepteur).
  2. Des courbes A et B quelle est celle qui correspond à la tension aux bornes du condensateur ? Justifier.
  3. Evaluer graphiquement la durée pour charger complétement le condensateur.
  4. Quelle expérience proposer vous pour charger moins vite le condensateur ? Représenter sur la figure l'allure du graphe obtenu.
  5. Etablir l'équation différentielle relative à uc, tension aux bornes du condensateur.
  6. Montrer que uc = E[1-exp(-t/t)] est solution de l'équation différentielle si t correspond à une expression que l'on déterminera.
  7. Calculer la valeur du rapport uc/E si t=t. Déterminer t graphiquement.
  8. Calculer uc/E si t=5t. Comparer ce résultat à celui de la question 3 et conclure.
  9. Etablir l'expression de i(t). En déduire l'allure de la courbe i(t) en précisant sa valeur initiale I0.
    - L'allure de cette courbe pourait être fournie par une tension. Laquelle ? Cette tension est-elle observable avec le montage proposé ?
    - Refaire un schéma modifié permettant d'observer cette tension et la tension aux bornes du circuit RC, en précisant les branchements de l'oscilloscope.
  10. Lorsque le condensateur est totalement chargé on ouvre l'interrupteur K et on court-circuite le dipole RC en reliant par un fil les points B et M. Indiquer l'allure de la courbe montrant l'évolution temporelle de uc pendant la décharge, puis sur un autre graphique, l'allure de la courbe montrant l'évolution temporelle de l'intensité i(t).
    - Des deux grandeurs uc(t) et i(t), quelle est celle qui n'est pas une fonction continue du temps ?
    E= 6 V ; e-1 = 0,37 ; e(-5) = 0,0067.

corrigé
tensions mesurées sur chaque voie :

voie 1: uBM tension aux bornes du dipole RC ou bien tension E aux bornes du générateur de tension ; voie 2 : tension uDM aux bornes du condensateur.

la courbe A montre une tension constante uBM =E=6 V

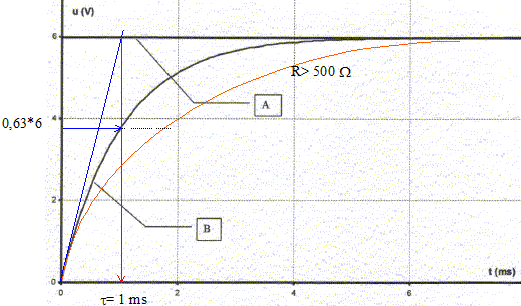
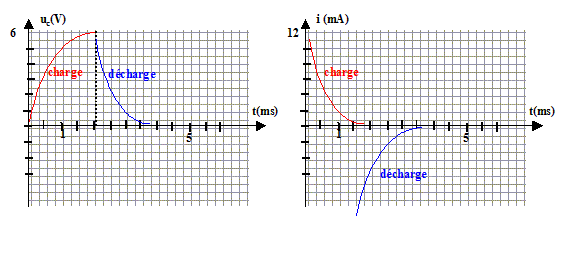
La courbe B visualise une tension croissante ( exponentielle) au cours du temps : tension uDM aux bornes du condensateur

durée pour charger complétement le condensateur : en fin de charge tension uDM aux bornes du condensateur = E = 6 V d'où la durée : 5,2 ms ( lecture graphe)

pour charger moins vite le condensateur, augmenter la constante de temps t= RC, donc prendre une plus grande valeur de R.

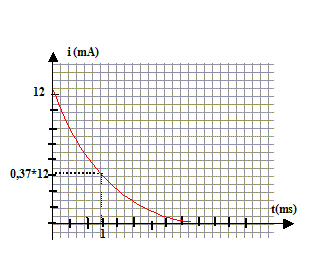
équation différentielle relative à uc: additivité des tensions : E=uAM = uAD+uDM = Ri + uc.

i = dq/dt et q=Cuc d'où i= Cduc/dt. E= RCduc/dt +uc. duc/dt +uc/t =E/t avec t =RC

uc = E[1-exp(-t/t)] ; duc/dt =E/t exp(-t/t) repport dans l'équation différentielle

E/t exp(-t/t) +E/t[1-exp(-t/t)] =E/(RC) vérifiée pout tout t si t=RC

si t=t : uc/E= 1-exp(-1)= 1-0,37 = 0,63 ; si t=5t : uc/E= 1-exp(-5)=1-0,0067 = 0,993

à t= 5t on peut considérer que la charge du condensateur est égale à 99 % de la charge complète.

expression de i(t) : i(t) = Cduc/dt =E/R exp(-t/t) = I0exp(-t/t) avec I0 = E/R = 6/500 = 12 mA

L'allure de cette courbe i(t) pourait être fournie par la tension aux bornes du résistor au facteur R près : la tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles.

L'intensité est une fonction discontinue. La tension uc est une fonction continue.

retour -menu