|
Résistance d'une bobine réelle. d'après bac S Polynésie 2006 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
|
|||
|
|
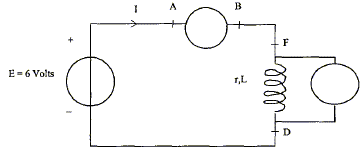
On désire vérifier la résistance r d'une bobine réelle d'inductance L= 250 mH modélisée par : 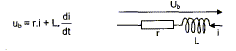 A- En régime permanent : On réalise un circuit comportant un générateur de tension continue de fem E= 6,0 V, de résistance interne négligeable, un ampèremètre numérique, un voltmètre numérique, des fils de connexion et la bobine étudiée.
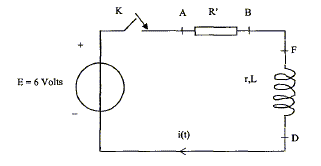
B- En régime transitoire : On ajoute en série au montage précédent une résistance R'= 10,0 W. Il remplace les appareils de mesures par un système d'acquisition informatisé qui lui donne les variations de i(t) obtenues à la fermeture de l'interrupteur. La tension du générateur reste égale à 6 V.
C- En régime transitoire : Cette bobine est branchée aux bornes d'un condensateur C= 4 mF préalablement chargé : 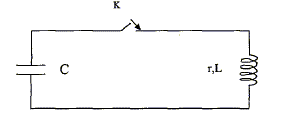
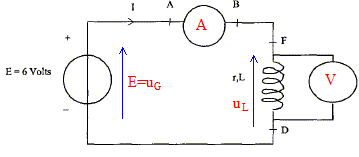
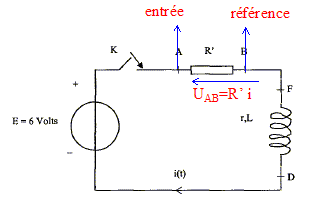
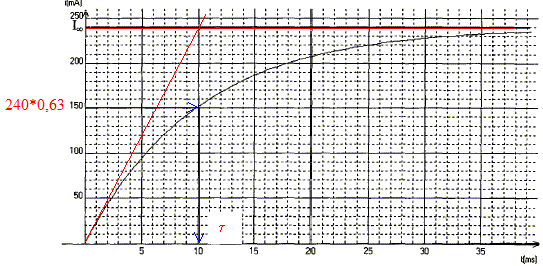
En régime permanent l'intensité I0 est constante et dI0/dt est nulle ; la tension aux bornes de la bobine est uL=rI0 uL=rI0 ; r = uL /I0 = 5,95 / 0,410 = 14,5 W. Phénomène observé dans le circuit en régime transitoire : à la fermeture de l'interrupteur, on observe un retard à l'établissement du courant ; pendant ce temps la bobine inductive stocke de l'énergie. Schéma du circuit permettant de visualiser une tension proportionnelle à l'intensité du courant : La tension aux bornes d'un résistor noté R' et l'intensité qui le traverse sont proportionnelles.
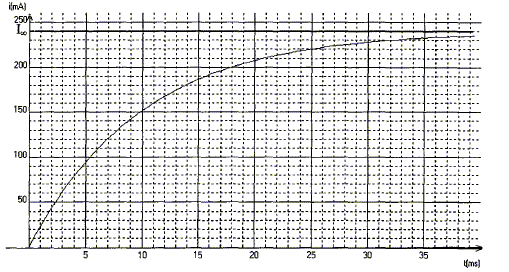
valeur de la constante de temps t = 10 ms = 10-2 s.
expression littérale de t = L/(R'+r)= L/R avec R= R'+r. dimension de t : E=½Li² soit L=2E/i² : énergie / intensité au carré Energie dissipée dans un résistor : E= Ri²t soit R = E/(i²t) : énergie / ( intensité² * temps) d'où L/((R0+r) a la dimension d'un temps valeur de r si L= 0,250 H ; t = 0,0100 s et R' = 10,0 W : r +R' = L/t = 0,25/0,01 = 250 soit r = 15,0 W. régime de fonctionnement de la bobine à t >5t : régime permanent En régime permanent l'intensité Ioo est constante et dIoo/dt est nulle ; la tension aux bornes de la bobine est uL=rIoo uL=rIoo ; uAB= R'Ioo ; additivité des tensions E=uL+uAB=rIoo +R'Ioo ; r +R'= E /Ioo = 6 / 0,24 = 25,0 W ; r= 15,0 W. les trois valeurs obtenues pour r sont cohérentes ( écart relatif 0,5*100/15 = 3,3 %) période propre de l'oscillateur LC : T0 = 2p(LC)½. valeur de T0 si L= 0,250H et C= 4 10-6 F T0 = 6,28(0,25*4 10-6)½=6,28*10-3s. ( 6 ms, le calcul donne un résultat peu précis, la capacité étant exprimée avec un seul chiffre significatif ) Amortissement des oscillations : lors des échanges d'énergie entre condensateur et bobine, une partie de l'énergie est dissipée par effet joule dans les conducteurs ohmiques. Encadrement de la pseudo-période T mesurée si 2 T appartient à l'intervalle [6,2 ; 6,4ms] T est comprise entre 6,1 et 6,2 ms, valeur cohérente avec la valeur de la période propre T0 ( écart relatif 0,15 *100/ 6,15 = 2,5%).
|
||
| |
|||
| |
|||
|
|