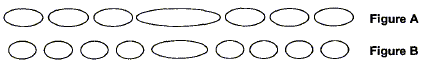|
Résistance d'une bobine réelle, où il est question de la lumière , hydrolyse d'un ester d'après bac S Polynésie 2006 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
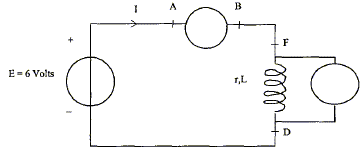
On désire vérifier la résistance r d'une bobine réelle d'inductance L= 250 mH modélisée par : 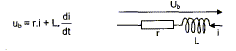 A- En régime permanent : On réalise un circuit comportant un générateur de tension continue de fem E= 6,0 V, de résistance interne négligeable, un ampèremètre numérique, un voltmètre numérique, des fils de connexion et la bobine étudiée.
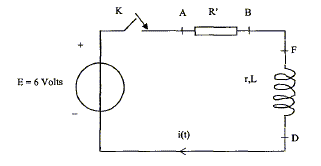
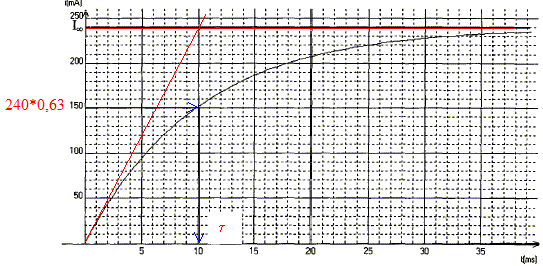
B- En régime transitoire : On ajoute en série au montage précédent une résistance R'= 10,0 W. Il remplace les appareils de mesures par un système d'acquisition informatisé qui lui donne les variations de i(t) obtenues à la fermeture de l'interrupteur. La tension du générateur reste égale à 6 V.
C- En régime transitoire : Cette bobine est branchée aux bornes d'un condensateur C= 4 mF préalablement chargé : 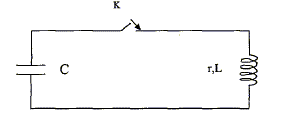
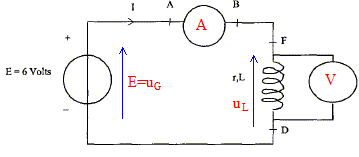
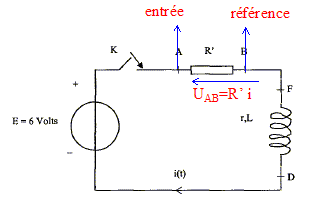
En régime permanent l'intensité I0 est constante et dI0/dt est nulle ; la tension aux bornes de la bobine est uL=rI0 uL=rI0 ; r = uL /I0 = 5,95 / 0,410 = 14,5 W. Phénomène observé dans le circuit en régime transitoire : à la fermeture de l'interrupteur, on observe un retard à l'établissement du courant ; pendant ce temps la bobine inductive stocke de l'énergie. Schéma du circuit permettant de visualiser une tension proportionnelle à l'intensité du courant : La tension aux bornes d'un résistor noté R' et l'intensité qui le traverse sont proportionnelles.
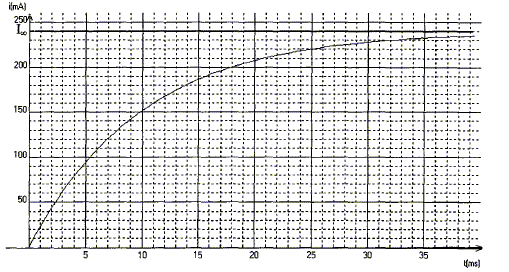
valeur de la constante de temps t = 10 ms = 10-2 s.
expression littérale de t = L/(R'+r)= L/R avec R= R'+r. dimension de t : E=½Li² soit L=2E/i² : énergie / intensité au carré Energie dissipée dans un résistor : E= Ri²t soit R = E/(i²t) : énergie / ( intensité² * temps) d'où L/((R0+r) a la dimension d'un temps valeur de r si L= 0,250 H ; t = 0,0100 s et R' = 10,0 W : r +R' = L/t = 0,25/0,01 = 250 soit r = 15,0 W. régime de fonctionnement de la bobine à t >5t : régime permanent En régime permanent l'intensité Ioo est constante et dIoo/dt est nulle ; la tension aux bornes de la bobine est uL=rIoo uL=rIoo ; uAB= R'Ioo ; additivité des tensions E=uL+uAB=rIoo +R'Ioo ; r +R'= E /Ioo = 6 / 0,24 = 25,0 W ; r= 15,0 W. les trois valeurs obtenues pour r sont cohérentes ( écart relatif 0,5*100/15 = 3,3 %) période propre de l'oscillateur LC : T0 = 2p(LC)½. valeur de T0 si L= 0,250H et C= 4 10-6 F T0 = 6,28(0,25*4 10-6)½=6,28*10-3s. ( 6 ms, le calcul donne un résultat peu précis, la capacité étant exprimée avec un seul chiffre significatif ) Amortissement des oscillations : lors des échanges d'énergie entre condensateur et bobine, une partie de l'énergie est dissipée par effet joule dans les conducteurs ohmiques. Encadrement de la pseudo-période T mesurée si 2 T appartient à l'intervalle [6,2 ; 6,4ms] T est comprise entre 6,1 et 6,2 ms, valeur cohérente avec la valeur de la période propre T0 ( écart relatif 0,15 *100/ 6,15 = 2,5%).
|
||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||
|
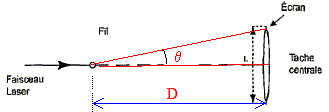
Partie A : Un faisceau de lumière parallèle monochromatique, de longueur d'onde l produit par une source laser arrive sur un fil vertical de diamètre a ( a est de l'ordre du dixième de mm). On place un écran à la distance D de ce fil ; D est très grande devant a. La figure ci-dessous est en vue de dessus. 
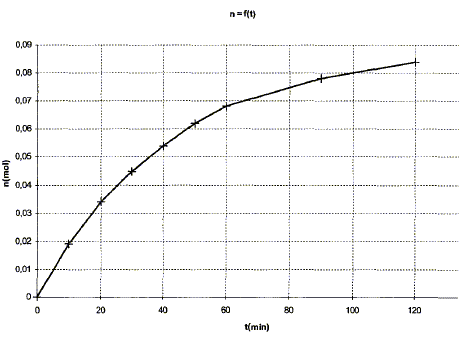
Partie B : On étudie la cinétique de la réaction en solution aqueuse, entre les ions permanganate MnO4- et l'acide éthanedioïque H2C2O4. L'équation de la réaction, considérée comme totale, modélisant la transformation chimique étudiée s'écrit : 2MnO4- + 5H2C2O4 +6H3O+ = 2Mn2+ + 10 CO2 +14 H2O. On suit l'évolution du système chimique par spectrophotométrie. En solution aqueuse les ions permanganate absorbent une partie des radiations du spectre visible contrairement à toutes les autres espèces du milieu réactionnel qui n'interagissent pas avec la lumière visible. Le spectrophotomètre est réglé sur la longueur d'onde l dans l'air de l'une des radiations absorbées par les ions permanganate. Il permet de mesurer l'absorbance A l de la solution. L'absorbance est proportionnelle à la concentration effective des ions permanganate soit Al(t) = k[MnO4-](t).
corrigé renseignement sur la nature de la lumière : Le phénomène de diffraction ( par une fente de largeur du même ordre de grandeur que la longueur d'onde de la lumière) met en évidence la nature ondulatoire de la lumière. écart angulaire q :
tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a avec : l longueur d'onde (m) et a : largeur de la fente (m) en tenant compte des deux relations ci-dessus : ½L/D=l/a soit L=2lD/a A chaque fil sa figure de diffraction :
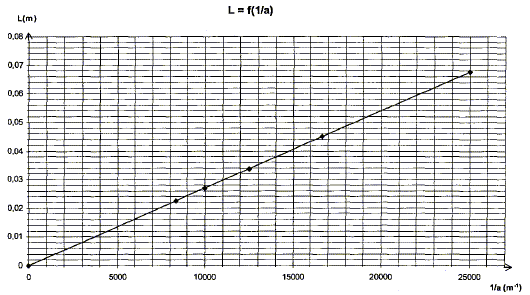
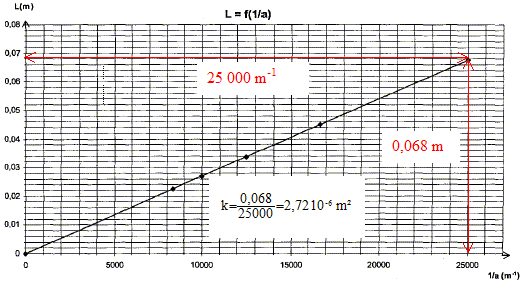
le produit lD étant constant, L largeur de la tache centrale et a largeur de la fente sont inversement proportionnelles : la figure A correspond donc à la plus petite fente a1= 60 mm et la figure B à la fente la plus large a2 = 80 mm. monochromatique : une lumière monochromatique correspond à une seule couleur, à une seule fréquence.
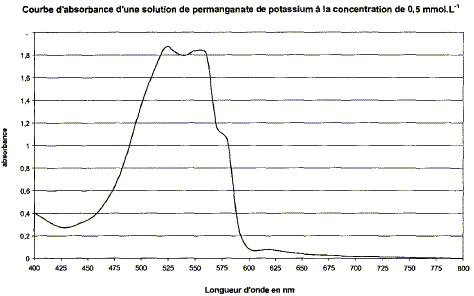
L= k * 1/a = 2,72 10-6 *1/a, en accord avec la realtion trouvée ci-dessus (L=2lD/a avec k identifié a : 2lD) longueur d'onde de la lumière : 2lD =2,72 10-6 avec D=2,5 m l =2,72 10-6 / 5 = 5,44 10-7 m = 544 nm. fréquence de cette lumière : f = c/l =3,00 108 / 5,44 10-7 =5,51 1014 Hz. A la traversée d'un milieu transparent dispersif : la fréquence reste constante( donc la couleur associée reste constante) ; la longueur d'onde varie ainsi que la célérité. Spectre d'absorption A=f(l) d'une solution de permanganate de potassium à 5,0 10-4 mol/L :
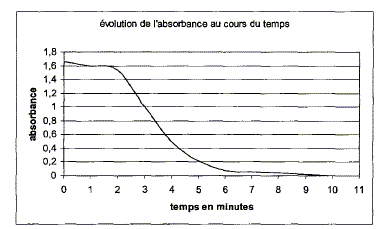
L'absorbance présente un maximum dans la région [480 nm - 580 nm] ; la solution absorbe le vert et une partie du jaune ; la solution a une teinte complémentaire de bande de couleur absorbée ; la solution est donc rose violet. Un laser de longueur d'onde 540 nm est tout a fait adapté pour l'étude spectrophotomètrique de la transformation. Evolution de l'absorbance A au cours du temps : l'ion permanganate MnO4- est la seule espèce colorée ; c'est de plus un réactif , donc qui disparaît au cours du temps ; en conséquence l'absorbance A diminue au cours du temps. Quantité de matière (mol) initiale des réactifs : volume (L) de la solution * concentration (mol/L) acide oxalique H2C2O4 :1,0 10-3*12,5 10-4 =1,25 10-6 mol. ion permanganate : 1,0 10-3*5 10-4 =5,0 10-7 mol. avancement maximal :
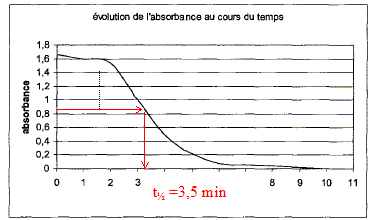
si H2C2O4 en défaut : 1,25 10-6-5xmax =0 soit xmax =2,5 10-7mol Evaluer la vitesse volumique à une date t : v= 1/V dx/dt avec V : volume de la solution et x : avancement (mol) l'absorbance A est proportionnelle à [MnO4-] ; or [ MnO4-] =(5,0 10-7-2x)/V dériver par rapport au temps : d[MnO4-]/dt = -2/V dx/dt ; soit 1/V dx/dt = -½d[MnO4-]/dt A la date t considérée, tracer la tangente à la courbe A=f(t) puis déterminer son coefficient direceteur ( -dA/dt) ; la vitesse v est proportionnelle à ce coefficient. Evolution de cette vitesse volumique : autocatalyse t<2 min : la vitesse est très faible, car le catalyseur ( l'un des produits Mn2+ ) est en faible quantité. 2<t<4 min : la vitesse augmente avec la quantité croissante du catalyseur. t>4 min : la vitesse diminue puis s'annule, car les quantités de matière des réactifs diminuent. temps de demi-réaction : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final ( dans ce cas l'avancement final est égal à l'avancement maximal) à t½ : x= 1,25 10-7 mol ; [ MnO4-]t½ =(5,0 10-7-2*1,25 10-7)/V = 2,5 10-7/V mol/L soit la moitié de sa valeur initiale donc l'absorbance a diminué de moitié à t½.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
s
corrigé 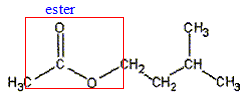
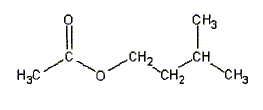
équation de la réaction associée à l'hydrolyse de l'ester : CH3-COO-CH2-CH2-CH(CH3)2 + H2O = CH3-COOH + (CH3)2CH-CH2-CH2OH CH3-COOH : acide éthanoïque ( groupe acide carboxilique -COOH) (CH3)2CH-CH2-CH2OH : 3-méthylbutan-1-ol ( alcool primaire groupe -CH2OH) équation associée à la réaction acido-basique de titrage : CH3-COOH + HO- = CH3-COO- + H2O Expression de la constante d'équilibre : K= [ CH3-COO-]éq / [HO- ]éq[CH3-COOH]éq ; Or CH3-COOH + H2O = CH3-COO- + H3O+ Ka = [ CH3-COO-]éq [H3O+ ]éq / [CH3-COOH]éq soit [ CH3-COO-]éq/ [CH3-COOH]éq = Ka /[H3O+ ]éq repport dans K : K = Ka /( [H3O+ ]éq [HO- ]éq) = Ka /Ke =1,8 10-5 / 10-14 = 1,8 109. équivalence : à l'équivalence les quantités de matière des réactifs mis en présence sont en proportions stoechiomètriques ; avant l'équivalence l'acide est en excès; après l'équivalence l'ion hydroxyde est en excès. Quantité de matière d'acide ( nA) présent à la date t : nA = CB VB éq. Quantité de matière d'acide ( n) formé dans le milieu initial à la date t : on a réparti le milieu réactionnel en 10 béchers d'où n = 10 nA = 10CB VB éq. caractéristiques d'une réaction d'hydrolyse : lente, athermique, limitée par la réaction inverse, l'estérification Quantités de matière initiales des réactifs : masse (g) = volume (mL) * masse volumique (g/mL) puis mase (g) / masse molaire (g/mol) n0 eau = 35*1/18 = 1,94 mol ; n0 ester = 15*0,87/130 =0,10 mol tableau d'avancement :
de plus xmax = 0,10 mol ( ester : réactif limitant) t1 = xf /xmax = 0,084/0,1 = 0,84 ( 84 %)
On peur augmentet t1 en éliminant l'un des réactif au fur et à mesure qu'il se forme (distillation par exemple quand cela est possible) on peut aussi ajouter l'un des réactifs ( le moins couteux : l'eau ) en grand excès : on déplace alors l'équilibre vers la droite, dans le sens de la consommation de ce réactif ajouté en large excès.
|
|||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||
|
|