Dispositif d'étude :

On utilise une corde métallique, de masse linéique µ = 4,35 10^-4 kg.m^-1 qu'on installe sur un support creux qui pourra jouer le rôle de caisse de résonance. L'une des extrémités de la corde (C) passe sur une poulie qui permet d'y suspendre une masse m. L'autre extrémité est fixée en B. La célérité v des ondes mécaniques le long d'une corde soumise à une tension T (en N) et de masse linéique µ est donnée par la relation : v = (T/µ)^½.

La masse m suspendue en C soumet la corde à une tension T = mg

Données : AB = 0,75 m et g = 9,80 N.kg^-1

On utilise une masse marquée m = 4,0 kg pour mettre le dispositif sous tension et on pince alors la corde en son milieu, on déclenche ainsi une vibration de la corde dans sa partie libre AB, ce qui génère un son.

1. Calculer la célérité des ondes mécaniques v₁ dans cette corde.
   Dans ces conditions, la corde émet-elle un son pur ou un son composé ?
   À quel mode propre de vibration de cette corde correspond la fréquence fondamentale f₁du son perçu ?
   Exprimer la relation entre la fréquence f₁ du son perçu et la longueur L = AB de la corde, sachant que dans ce cas elle vibre selon un seul fuseau. Calculer la valeur de f₁.
2. On souhaite obtenir, en déclenchant une vibration sonore de la même manière, un son émis plus grave. On dispose de deux masses marquées supplémentaires de valeurs m₁= 2,0 kg et m₂ = 7,0 kg.
   La fréquence f₂ du nouveau son sera-t-elle supérieure ou inférieure à f₁?
   En déduire comment la nouvelle célérité v₂ doit se situer par rapport à v₁.
   Par quelle masse marquée faut-il donc remplacer m pour obtenir un son plus grave ? Justifier la réponse.

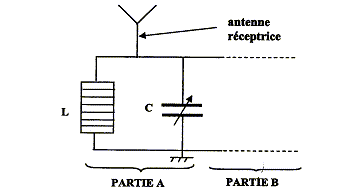
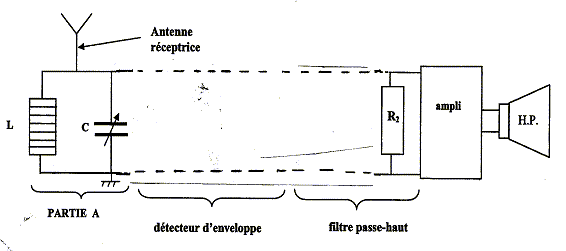
Propagation hertzienne :

Un poste de radio situé à proximité de l'expérimentateur émet, pendant quelques instants, un son identique celui obtenu par l'appareil de la partie 1.

On considère dans la suite de l'exercice que la fréquence de ce son est égale à f₁= 200 Hz.

Dans cette partie, on étudie le processus de réception correspondant. Le signal sonore émis par le haut-parleur résulte de la réception d'une onde électromagnétique de fréquence F par l'antenne du poste de radio.

1. Quel est le type de signal généré dans l'antenne réceptrice par les ondes électromagnétiques qu'elle reçoit ?
2. À la base de l'antenne, on identifie l'élément de circuit suivant, dans lequel on trouve une bobine d'inductance L et un condensateur de capacité réglable C. Le bouton de réglage de C commande également le curseur d'affichage du poste de radio. Dans notre exemple, ce curseur pointe sur 10 kHz
   

   Quel est le rôle de la partie A du circuit, relativement aux signaux électriques issus de l'antenne ?
   Dans la situation décrite, quelle est la valeur de la fréquence du signal électrique qui se propage dans la partie B du circuit ?

3. On considère que le signal sonore émis par le haut parleur a les mêmes caractéristiques que le signal électrique qu'il reçoit. On réalise l'enregistrement du son dont il est question dans cette partie à l'aide d'un système d'acquisition muni d'un microphone et on obtient la courbe suivante.

   .-Cet enregistrement est-il conforme à votre réponse à la question 1.1.1. ? Justifier la réponse.
   - Mesurer et vérifier que la période T_l du signal enregistré est en accord avec la valeur de f₁.

4. Pour obtenir le signal émis par le haut-parleur à partir du signal qui se propage dans la partie B, il est nécessaire de démoduler ce dernier. La partie B du circuit contient donc :
   a) un détecteur d'enveloppe, constitué à partir d'un condensateur C_l, d'un conducteur ohmique R₁ et d'une diode D.
   b) un filtre passe-haut, constitué à partir d'un condensateur C₂ et d'un conducteur ohmique R₂.
   compléter convenablement la partie B du circuit avec C₁, R₁, D et C₂ de manière à assurer une bonne démodulation du signal reçu dans la partie A.

---

---

corrigé

---

célérité des ondes mécaniques v₁ dans cette corde : v = (T/µ)^½.

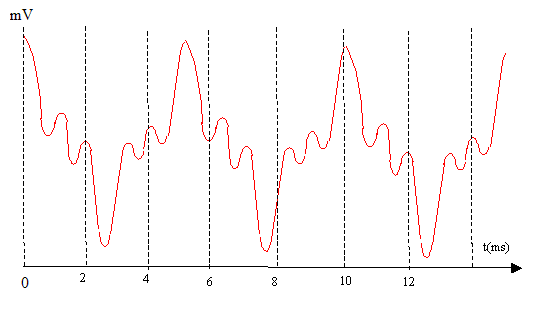
T= mg = 4,0*9,81 N ; m= 4,35 10^-4 kg m^-1 ; d'où v = (4*9,81/ 4,35 10^-4 )^½=3,0 10² m/s.
Dans ces conditions, la corde émet un son composé du mode fondamental et des modes harmoniques.
mode propre de vibration de cette corde correspond la fréquence fondamentale f₁du son perçu : mode fondamental
relation entre la fréquence f₁ du son perçu et la longueur L = AB de la corde, sachant que dans ce cas elle vibre selon un seul fuseau :

La corde est le siège d'ondes stationaires si sa longueur L est un multiple de la demi-longueur d'onde : L= ½nl avec n entier.

n= 1 pour le mode fondamental ; de plus l = v/f ₁ d'où : f ₁ = v / l = v / (2L)

valeur de f₁ = 300/(2*0,75) = 2,0 10² Hz.

---

un son plus grave aura une fréquence f₂ inférieure à f₁.

nouvelle célérité v₂ située par rapport à v₁ :

d'une part : f₁= v₁/(2L) et f₂= v₂/(2L) et d'autre part f₂ inférieure à f₁ d'où v₂< v₁.

masse marquée m pour obtenir un son plus grave :

d'une part v₂< v₁ et d'autre part : v = (mg/µ)^½ d'où m<4 kg ( par exemple m₁= 2,0 kg)

---

Propagation hertzienne :

type de signal généré dans l'antenne réceptrice par les ondes électromagnétiques : signal électrique modulé en amplitude

rôle de la partie A du circuit, relativement aux signaux électriques issus de l'antenne :

accorder le récepteur sur la fréquence de la station émettrice choisie.

valeur de la fréquence du signal électrique qui se propage dans la partie B du circuit : 10 kHz.

Cet enregistrement correspond à un son composé périodique : il est donc en accord avec la réponse a la question 1.

période T_l du signal enregistré : d'après le graphe 2 périodes correspondent à 10 ms

T_l = 5 ms = 5 10^-3 s d'où la fréquence : 1/T = 200 Hz est en accord avec la valeur de f₁.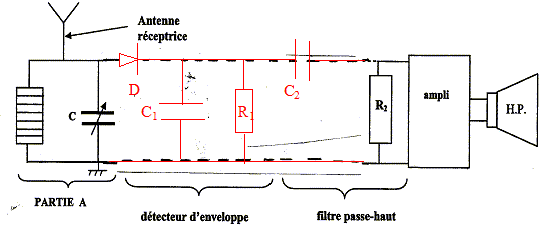

---

---