|
analogies électromécaniques. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||||||||||||
|
||||||||||||||||
|
|
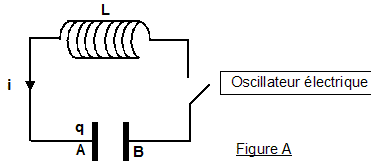
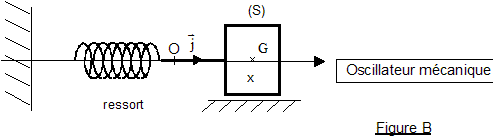
On considère les deux oscillateurs idéaux suivants (voir figures A et B ci-dessus) : un circuit électrique comprenant : - une bobine d'inductance L et de résistance négligeable ; un condensateur de capacité C et d'armatures A et B; un interrupteur. Les conventions d'orientation sont telles que l'intensité du courant est i = dq/dt , q(t) étant la charge instantanée du condensateur, c'est-à-dire celle de l'armature A. Les conditions initiales du fonctionnement sont les suivantes: à t négatif ou nul, l'interrupteur est ouvert et le condensateur porte la charge q(0) = Q0 à t = 0, on ferme l'interrupteur. On donne L= 0,10 H ; C = 10,0 µF et Q0= 10-4 C. ·un système {solide - ressort} horizontal comprenant : - un solide (S), de masse m et de centre d'inertie G, glissant sans frottement dans la direction de l'axe O horizontal et d'origine O (voir Figure B) : si (S) est au repos, G est en O ; à un instant quelconque, G est repéré par son abscisse x - un ressort à spires non jointives de raideur k, de masse négligeable, dont l'une des extrémités est attachée à (S) et l'autre fixée rigidement à un support. Les conditions initiales choisies sont les suivantes: à l'instant t = 0, la position du centre d'inertie du solide vaut X0 et sa vitesse vx est nulle. On donne le rapport m/k=1,0.10-2 S.I. et X0 = + 4,0 cm. I- Oscillateur mécanique On admet que l'équation différentielle vérifiée par x(t) est md²x/dt² +kx=0 où d²x/dt² désigne la dérivée seconde par rapport au temps de la fonction x(t).
II- Oscillateur électrique On admet que l'équation différentielle vérifiée par la charge q(t) est : Ld²q/dt² +q/C=0 On utilise de façon systématique la comparaison entre les deux équations différentielles.
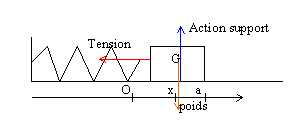
(S) est soumise à son poids, vertical, vers le bas, valeur mg, à l'action du support, opposée au poids et à la tension du ressort, horizontale, valeur T=kx
équation différentielle du mouvement : écrire la seconde loi de Newton sur un axe horizontale orienté vers la droite -kx = md²x/dt² ou d²x/dt² + k/m x=0 Je vérifie que x = A.cos(2p t/T+j) est solution de l'équation différentielle : dériver x par rapport au temps : x' = -A2p /Tsin (2p t/T+j) ; x" = -A(2p /T)2 cos (2p t/T+j) = - (2p/T)2 x repport dans l'équation différentielle : - (2p /T)2 x + k/m x=0 doit être vérifiée quelque soit le temps d'où (2p/T)2= k/m soit T² = (2p)2 m/k ou T= 2p(m/k)½. unité du rapport m/k : 2p est sans dimension et T , période exprimée en seconde donc m/k s'exprime en s2. valeur numérique : T= 6,28 ( 10-2)½= 0,63 s. En prenant en compte les conditions initiales du début de l'énoncé : x(0) = X0 . A cos(j) = X0 positif conduit à : A= X0 et j = 0. ou encore sachant que la vitesse initiale est nulle : x'= -A2p /Tsin (2p t/T+j) ; x'(0)= -A2p /Tsin (j) = 0 avec A différent de zéro sin (j) =0 donne j =0 ou j =p ; cette dernière valeur ne peut pas être retenue car A est positif.
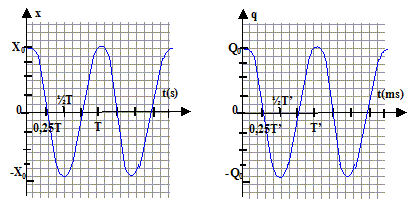
l'intensité correspond à la vitesse. En utilisant les similitudes entre les équations différentielles et les conditions initiales x(0) = X0 et q(0)= Q0 : v(t) = x'(t) = -A2p /Tsin (2p t/T) et i(t) = dq/dt conduisent à dq/dt = -A2p /Tsin (2p t/T) par intégration la charge instantanée du condensateur vaut : q(t) = Acos (2p t/T) avec A= charge initiale = Q0 expression de T' en fonction des caractéristiques des composants du circuit : T' = 2p(LC)½. valeur numérique : T' = 6,28 (0,1 10-5)½=6,3 10-3 s. les fonctions x(t) et q(t):
Les oscillateurs réels ne sont pas idéaux : pertes d'énergie ( sous forme de chaleur ) respectivement lors des frottements mécaniques, lors du passage du courant dans les conducteurs électriques (effets joule).
|
|||||||||||||||
| |
||||||||||||||||
| |
||||||||||||||||
|
|