Les instruments de musique sont de formes et de dimensions
très variées ; ils sont aussi constitués de matériaux très divers.
Cependant, tous fonctionnent sur le même principe : les sons qu'ils
produisent sont le résultat d'une vibration qui se transmet jusqu'à
l'oreille. On peut les classer en trois familles qui sont les cordes,
les vents et les percussions. Dans le cas des instruments à cordes, il
existe deux techniques de production du son : corde frottée et corde
pincée.
Dans cet exercice, on étudie le son produit par une corde
vibrante, puis on compare les sons produits par l'une des cordes d'un
violoncelle, la corde appelée "corde de sol", selon qu'elle est frottée
ou pincée en utilisant un archet. Cette corde de longueur utile L =
69,0 cm est fixée à ses deux extrémités sur l'instrument.
Aucune connaissance musicale préalable n'est nécessaire pour
résoudre cet exercice.
- Le son produit par la corde frottée :
Le violoncelliste frotte la corde avec son archet pour la mettre en
vibration. Ainsi excitée, la corde peut vibrer selon plusieurs modes.
- Comment appelle-t-on les modes de vibration de la corde de longueur L
?
- Observation de la corde vibrante à la lumière du jour.
Décrire l'aspect de la corde vibrant dans son mode fondamental quand on
l'observe à la lumière du jour et l'illustrer par un schéma sans souci
d'échelle.
Calculer la longueur d'onde l correspondant
au mode fondamental.
- Le son produit par la corde est étudié à l'aide d'un microphone
branché à un oscilloscope numérique. L'oscillogramme correspondant est
donné à la figure 7 ci-dessous.
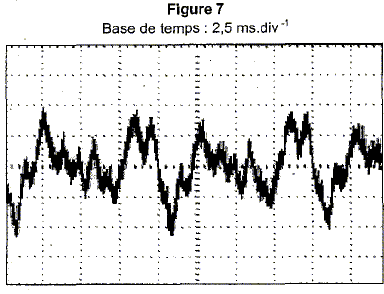
Exploiter cet oscillogramme pour déterminer la fréquence f1
du mode fondamental.
A quelle qualité physiologique du son est associée cette fréquence ?
- Décrire la méthode qui permet de retrouver la fréquence du mode
fondamental en utilisant un stroboscope.
- Déduire des réponses aux questions précédentes la célérité v de la
vibration le long de cette corde.
- On réalise une analyse spectrale du son produit par cette corde
vibrant sur toute sa longueur. Le spectre de fréquences est représenté
à la figure 8 ci-dessous. Sur ce spectre sont repérés cinq pics notés
(a), (b), (c), (d), et (e). On note f2 et f3 les
fréquences des deux harmoniques immédiatement supérieures à la
fréquence fondamentale f1.
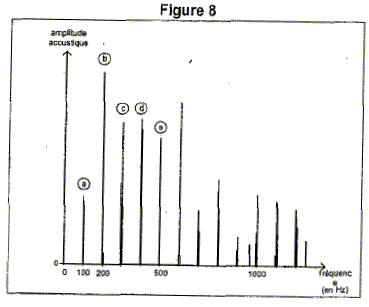
Ecrire la relation existant entre f2 et f1
d'une part ; entre f3 et f1 d'autre part.
Retrouver parmi ces cinq pics, celui qui correspond au mode fondamental
de fréquence f1 et préciser ceux qui correspondent à f2
et f3.
- Pour jouer la note à l'octave supérieure, le violoncelliste excite la
corde avec l'archet tout en appuyant franchement en son milieu, ce qui
revient à diviser la longueur L de la corde par deux. On rappelle que
la fréquence du son produit est inversement proportionnelle à la
longueur de la corde. Donner, en fonction de f1,
l'expression de la fréquence f ' du fondamental du son produit lorsque
le violoncelliste joue la note à l'octave supérieure.
- Le son produit par la corde pincée :
Par une autre technique appelée "pizzicato", le
violoncelliste pince maintenant la corde de sol pour la mettre en
vibration. L'oscillogramme correspondant au son émis par la corde en
appliquant la technique "pizzicato" est donné à la figure 9 ci-dessous.
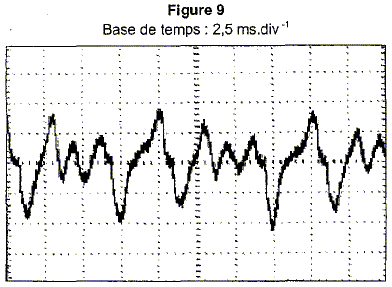
Exploiter la figure 9 ci-dessus pour indiquer si la
hauteur du son est modifiée par rapport à celle du son étudié à la
question 1.
En comparant les figures 7 et 9 ci-dessus, indiquer la caractéristique
physiologique du son qui a ainsi été modifiée. Justifier la réponse.
- Une autre technique avec la corde frottée :
Pour tirer de son instrument des sons particuliers, le
violoncelliste excite avec son archet la corde qu'il effleure avec
l'autre main en son milieu.
On donne le spectre du son produit de cette manière à la
figure 10 ci-dessous.
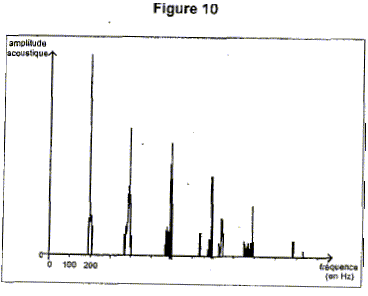
En comparant les spectres des figures 8 et 10 ci-dessus,
indiquer la conséquence de cette technique sur les caractéristiques
physiologiques du son produit dans les deux situations correspondantes.
corrigé
Le son produit par la
corde frottée :
Les modes propres de vibration de
la corde de longueur L s'appelle mode fondamental ( n=1) et harmoniques
( n>1)
aspect de la corde vibrant dans son mode fondamental quand
on l'observe à la lumière du jour :
d'une part cette corde de longueur utile L = 69,0 cm est fixée
à ses deux extrémités sur l'instrument.
d'autre part vibration dans le mode fondamental ( n=1)
en conséquence on observe un seul fuseau présentant un noeud
de vibration à chaque extrémité.

longueur d'onde l correspondant au mode
fondamental : l = 2L = 2*0,690 = 1,38 m.
fréquence f1
du mode fondamental :
période T : 0,01 s ; f1 = 1/T = 100 Hz.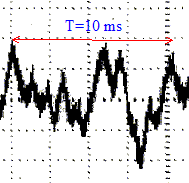
qualité physiologique du son : cette fréquence est
associée à la hauteur du son.
méthode qui permet de retrouver la fréquence du mode
fondamental en utilisant un stroboscope :
éclairé la corde vibrante avec la lumière émise par un
stroboscope ; rechercher la plus petite fréquence du stroboscope
conduisant à l'immobilité apparente de la corde.
célérité v de la vibration le long de cette corde :
v = lf = 1,38*100 = 138 m/s.( 1,4 102 m/s deux chiffres
sigificatifs pour la valeur de la fréquence)
relation existant entre f2
et f1 d'une part ; entre f3 et f1
d'autre part :
pic a : mode fondamental ( 100 Hz) ; f2 = 2 f1
= 200 Hz ( pic b) ; f3 =3 f1 = 300 Hz ( pic c).
expression de la fréquence f ' du fondamental du son
produit lorsque le violoncelliste joue la note à l'octave supérieure.
d'une part "en appuyant franchement en son milieu, ce qui
revient à diviser la longueur L de la corde par deux".
d'autre part la fréquence du son produit est inversement
proportionnelle à la longueur de la corde.
d'où f' = 2 f1.
Le son produit par la
corde pincée :
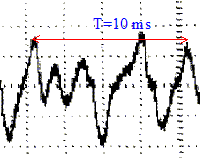
la fréqence du fondamental est identique donc : la hauteur du
son n'est pas modifiée par rapport à celle du son étudié à la question
1.
Néanmoins les deux oscillogrammes de ces sons complexes sont différents
: on aura sans doute des harmoniques différentes : en conséquence le
timbre du son a ainsi été modifiée.
Une autre technique avec
la corde frottée :
En comparant les spectres des figures 8 et 10 ci-dessus,
conséquence de cette technique sur les caractéristiques physiologiques
du son produit dans les deux situations correspondantes :
figure 8 : la fréquence du mode fondamental est 100 Hz
figure 9 : les fréquences correspondantes aux pics du spectre
sont des multiples de 200 Hz : donc la fréquence du fondamental est 200
Hz et la hauteur du son est modifiée par cette technique.





