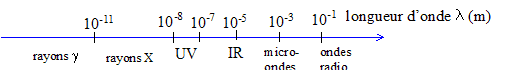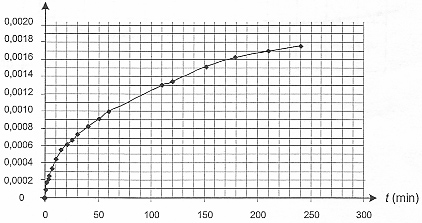
L'aquariophilie est une passion qui touche de plus en plus d'amateurs mais aussi de néophytes. De nombreux facteurs peuvent contribuer à un déséquilibre dangereux pour la vie et la santé des poissons. Il est donc nécessaire de contrôler régulièrement la qualité de l'eau. Le pH de l'eau est la première grandeur qu'il faut mesurer, au moins une fois par semaine, et ajuster éventuellement. En effet, certains poissons ne peuvent évoluer que dans un milieu acide (c'est le cas des poissons d'Amazonie comme les Néons ou les Tétras), d'autres dans un milieu basique (c'est le cas des poissons d'Amérique Centrale comme les Platy et les Molly). Aucun de ces poissons ne tolère une trop forte teneur en ions ammonium (NH₄⁺) ou en ions nitrite (NO₂^-) : le cycle de l'azote doit donc être surveillé en évitant soigneusement la surpopulation de l'aquarium et l'excès de nourriture. D'après "Poissons et aquariums" - Édition Larousse

L'exercice suivant est destiné à préciser certains points de ce texte. On étudie d'abord un produit commercial utilisé pour diminuer le pH de l'eau de l'aquarium ; on s'intéresse ensuite à la formation des ions ammonium. Les parties 1. et 2. sont indépendantes.

I- Étude d'une solution commerciale destinée à diminuer le pH de l'aquarium :

Sur l'étiquette du produit on peut lire que la solution commerciale S₀ est constituée d'acide chlorhydrique (H₃O⁺ + Cl ^- (aq)) mais aucune concentration n'est indiquée. La transformation conduisant à l'acide chlorhydrique étant totale, la concentration c₀ de la solution commerciale est égale à la concentration en ions H₃O⁺. On cherche à déterminer cette concentration en faisant un titrage pH-métrique. Pour cela on dilue 50 fois la solution commerciale et on procède au titrage d'un volume V_A = 20,0 mL de la solution diluée S_A à l'aide d'une solution d'hydroxyde de sodium S_B (Na⁺(aq) + HO ^- (aq)) de concentration molaire en soluté apporté c_B = 4,0 10 ^-2 mol.L^-1. On obtient la courbe ci-dessous. On a également fait apparaître la courbe représentant la dérivée du pH en fonction du volume de soude versé.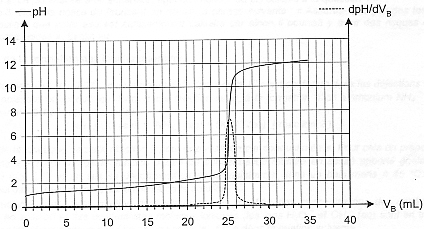

Aide au calcul : log 8= 0,9; log 5 = 0,7; 10^6,4 = 2,5 10⁵ ; 10 ^-6,4 = 4,0 10 ^{- 7}

1. Écrire l'équation de la réaction support du titrage.
2. Équivalence : - Définir l'équivalence. En déduire la valeur de la concentration des ions oxonium dans la solution diluée S_A. Montrer que dans la solution commerciale, la concentration des ions oxonium [H₃O⁺] est voisine de 2,5 mol.L^-1 . Cette valeur sera utilisée pour la suite de l'exercice.
3. On désire diminuer le pH de l'eau de l'aquarium et l'amener à une valeur proche de 6 alors qu'il était initialement égal à 7. Sur le mode d'emploi du fabricant on peut lire qu'il faut verser, en une fois, 20 mL de la solution commerciale dans 100 L d'eau. Pour simplifier le calcul, on considérera que le volume final reste égal à 100 L.Quelle serait la valeur du pH final de l'eau de l'aquarium s'il n'y avait qu'une simple dilution des ions H₃O⁺ ?
4. L'eau étant toujours plus ou moins calcaire, elle contient des ions hydrogénocarbonate (HCO₃^-(aq)) dont il faut tenir compte. Les ions H₃O⁺ introduits vont, en effet, réagir avec ces ions. L'équation associée à la réaction considérée est la suivante :

   HCO₃^-(aq) + H₃O⁺ = CO₂ (aq) + 2 H₂O (l ) ( réaction 1 )
   - Donner l'expression de la constante d'équilibre K₁ associée à l'équation de la réaction 1 en fonction des concentrations des différentes espèces chimiques présentes. Exprimer cette constante d'équilibre en fonction de la constante d'acidité K_A du couple : CO₂(aq), H₂O / HCO₃^-(aq). Déterminer sa valeur numérique. Donnée : K_a = 10^-6,4.

5. L'eau utilisée pour l'aquarium est très calcaire. Dans cette eau, les concentrations molaires initiales des espèces mises en jeu dans la réaction 1 sont telles que le quotient de réaction initial de cette réaction vaut : Q_r,i = 5,0. En utilisant le critère d'évolution spontanée, montrer que des ions H₃O⁺ sont consommés si l'eau est calcaire.
   - Le pH final sera-t-il supérieur, égal ou inférieur au pH calculé à la question 1.3. ?
   - Dans la notice du fabricant on trouve la phrase suivante : "Assurez-vous par des tests réguliers que votre eau est suffisamment calcaire car sinon il pourrait y avoir des risques de chutes acides ". Expliquer.

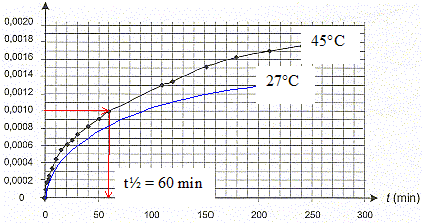
II- Étude de la formation des ions ammonium.

L'urée, de formule (NH₂)₂CO, est un polluant de l'aquarium. Elle est contenue dans les déjections de certains poissons et conduit, au cours d'une réaction lente, à la formation d'ions ammonium NH₄⁺ et d'ions cyanate OCN^- selon l'équation :

(NH₂)₂CO (aq) = NH₄⁺ (aq) + OCN^- (aq) (réaction 2)

L'étude de la cinétique de cette réaction 2 peut être réalisée par conductimétrie. Pour cela on prépare un volume V = 100,0 mL d'une solution d'urée de concentration molaire en soluté apporté égale à c = 0,20 mol.L^-1 et on suit sa décomposition en la maintenant dans un bain marie à 45 °C. À différentes dates, on mesure la conductivité de la solution. La conductivité s de cette solution peut s'exprimer en fonction des concentrations des espèces ioniques en solution et des conductivités molaires ioniques (les ions H₃O⁺ et HO^- (aq) sont en très faible quantité et pourront ne pas être pris en compte). On a donc la relation suivante :

s = l_NH4+[NH₄⁺] + l_OCN-[OCN^-]

1. Montrer que la concentration de la solution en ions NH₄⁺ (aq) peut être déterminée à partir de la mesure de la conductivité de la solution, les conductivités molaires ioniques étant connues.
2. Évolution du système chimique : établir littéralement le tableau descriptif de l'évolution du système.
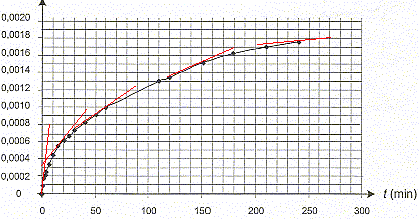
   - En déduire la relation, à chaque instant, entre la concentration en ions NH₄⁺ (aq) en solution et l'avancement de la réaction.
   - Calculer l'avancement maximal x_max.
3. On peut ainsi représenter l'évolution de l'avancement de la réaction en fonction du temps.

   En déduire le taux d'avancement de la réaction à l'instant de date t = 110 min.

4. La vitesse volumique de réaction est donnée par la relation : v(t) =1/V dx/dt où x est l'avancement de la réaction à l'instant de date t et V le volume de la solution. Décrire, en utilisant la courbe précédente, l'évolution de cette vitesse.
5. En poursuivant l'expérience pendant une durée suffisante, on obtient une concentration finale : [NH₄⁺]_f = 2,0 10 ^-2 mol.L^-1 .Déterminer le taux d'avancement final de cette transformation. Cette transformation est-elle totale ?
6. Définir puis déterminer graphiquement le temps de demi-réaction.
7. Dans l'aquarium, la valeur de la température est seulement de 27°C. Tracer sur la figure, l'allure de la courbe précédente à cette température.
8. Les ions ammonium finissent par se transformer en ions nitrate dont l'accumulation risque de compromettre la vie des poissons. Ces derniers ions constituent un aliment essentiel pour les plantes vertes de l'aquarium. Expliquer pourquoi dans les livres d'aquariophilie, on dit que l'aquarium doit être "bien planté".

    

A l'équivalence, la quantité de matière de l'espèce à titrer ( acide chlorhydrique) et la quantité de matière de l'espèce titrante ( hydroxyde de sodium ) mis en présence ont réagi en proportions stoéchiométriques. Avant l'équivalence la solution à titrer d'acide chlorhydrique est en excès dans le becher ; après l'équivalence la solution titrante de soude est en excès dans le bécher.

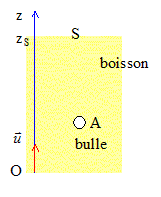
On se propose dans cet exercice de faire une plongée au cœur de l'effervescence d'une boisson gazeuse, d'illustrer et d'interpréter sous l'angle physico-chimique les différentes étapes de la vie éphémère d'une bulle, à savoir : sa naissance, son ascension dans le liquide, et son éclatement en surface. Dans tout l'exercice les bulles seront assimilées à des sphères, et la boisson à un liquide de masse volumique égale à celle de l'eau. Le référentiel d'étude est terrestre considéré comme galiléen.

Masses volumiques : eau r_e = 1,010³ kg.m^-3; dioxyde de carbone r_CO2 = 1,8 kg.m^-3 ; Intensité de la pesanteur: g = 10 m.s^-2.

I- Naissance et décollement d'une bulle :

Dans une bouteille fermée de boisson gazeuse, un équilibre s'établit entre le dioxyde de carbone qui est dissous dans la boisson et le dioxyde de carbone gazeux piégé dans le col de la bouteille. Lors de l'ouverture de celle-ci, l'équilibre est rompu et la boisson se débarrasse d'une partie du dioxyde de carbone dissous qui retourne progressivement en phase gazeuse. Il y a formation de bulles qui vont s'enrichir continûment en gaz au cours de leur remontée.

Dans un verre, les bulles naissent sur des sites de nucléation qui sont des embryons de bulles présents en solution ou de petites poches d'air piégées par des impuretés microscopiques (fibres de cellulose, microcristaux …). La figure 1 illustre cette formation de bulles sur un site de nucléation.

Dès que la valeur de la poussée d'Archimède à laquelle la bulle est soumise dépasse la valeur de la force capillaire qui l'ancre à son site de nucléation, la bulle se détache. Puis une autre bulle naît et subit le même sort.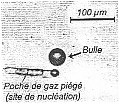

Pour une bulle qui vient de se détacher du site de nucléation dans un liquide de masse volumique r_e :

1. Donner la direction et le sens de la poussée d'Archimède qui s'exerce sur une bulle de volume V₀ dans la boisson.
2. Donner l'expression littérale de sa valeur en fonction du volume V₀ de la bulle.

II- Ascension d'une bulle : à la recherche d'une modélisation satisfaisante.

À l'instant de date t0 = 0 s, une bulle de rayon r0 = 20 mm, située au point A à la profondeur z0 = 0 m dans le repère (O ;z ) (figure 2) se détache de son site de nucléation avec une vitesse initiale v0 nulle dans le référentiel terrestre supposé galiléen. Elle remonte verticalement vers la surface S du liquide, qu'elle atteint avec une vitesse vS d'environ 15 cm.s-1. Dans un premier temps (pour les questions 2.1. et 2.2.), on assimile la bulle de gaz à une sphère dont le volume ne varie pas lors de sa remontée.

1. Étude du mouvement d'une bulle en l'absence de force de frottement :
   - Montrer que le poids P₀ de la bulle a une valeur négligeable devant celle de la poussée d'Archimède F_A en calculant le rapport : P₀ / F_A .
   - En utilisant la deuxième loi de Newton, établir l'expression de la coordonnée a_z du vecteur accélération de la bulle en fonction des masses volumiques r_e et r_CO2 et de g.
   - En déduire l'expression de la valeur de la vitesse de la bulle en fonction du temps.
   - Montrer que la durée t_s théoriquement nécessaire pour que la bulle atteigne la surface avec la vitesse v_s est alors d'environ trente microsecondes.
   - Cette valeur correspond-elle aux observations de la vie quotidienne ? Conclure quant à la validité du modèle proposé.
2. Étude du mouvement de la bulle en présence d'une force de frottement :
   Le liquide exerce sur la bulle une force de frottement, proportionnelle à sa vitesse, de valeur f = k v,, colinéaire et de sens contraire au vecteur vitesse. k est un coefficient qui dépend du rayon de la bulle et de la viscosité du fluide dans lequel elle se déplace.
   - Représenter schématiquement, sans souci d'échelle, les forces non négligeables qui s'exercent sur la bulle en mouvement après son décollement du site de nucléation.
   - En appliquant la deuxième loi de Newton, montrer que l'équation différentielle qui régit l'évolution de la vitesse de la bulle s'écrit alors :
   dv/dt + kv/(r_CO2 v₀) =r_e /r_CO2 g
   - En déduire l'expression littérale de la vitesse limite v_lim atteinte par la bulle.
   - L'application numérique donne v_lim voisin de 1 mm.s^-1. Compte tenu de cette valeur, conclure quant à la validité du modèle proposé.
3. Un autre paramètre à prendre en compte :
   Les modélisations précédentes ne décrivent pas de manière satisfaisante le mouvement de la bulle dans la boisson gazeuse. En particulier, les expériences réalisées dans du champagne montrent que la variation du volume de la bulle ne peut pas être négligée (figure 3). On se propose d'en trouver l'origine.

   On suppose que la quantité de matière n₀ de gaz présent dans la bulle et la température restent constantes. Dans ce cas, lors d'une remontée de 12 cm du point A à la surface S, la diminution de pression du gaz ne ferait augmenter son volume initial que de 2 %. Dans la réalité, l'augmentation du volume est un million de fois supérieure ! Un des deux paramètres supposés constants dans le texte précédent ne l'est donc pas.
   - En s'aidant d'une phrase du texte introductif à la partie 1 de cet exercice, expliquer pourquoi le volume de la bulle augmente si fortement lors de sa remontée.
   - Durant l'ascension le poids de la bulle est toujours négligeable devant la poussée d'Archimède. Sachant que le coefficient k défini à la question 2.2. augmente avec le rayon de la bulle, préciser qualitativement l'influence de la variation du volume de la bulle sur chacune des forces qui s'exercent sur elle au cours de la remontée.
   Des laboratoires spécialisés ont élaboré des modèles plus satisfaisants tenant compte de paramètres négligés précédemment.

III- L'éclatement des bulles en surface :

La bulle a maintenant gagné la surface et le film liquide qui constitue la partie émergée de la bulle s'amincit (figure 4.a) jusqu'à se rompre lorsque son épaisseur avoisine le micromètre. Le trou qui apparaît s'ouvre (figure 4.b) et la durée de disparition de la calotte sphérique n'est que de quelques dizaines de microsecondes ! Le cratère qui reste à la surface du liquide ne va pas durer (figure 4.c).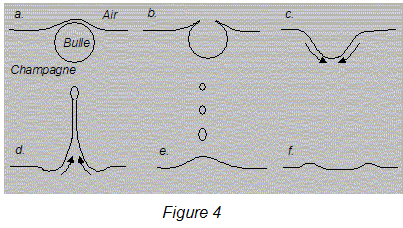

De violents courants apparaissent et, en se refermant, cette cavité projette vers le haut un mince jet de liquide (figure 4.d). Le jet se brise ensuite en fines gouttelettes (figure 4.e) qui en retombant dans le liquide engendrent des ondes circulaires centrées sur la "bulle-mère" (figure 4.f). Ces observations nécessitent l'utilisation d'une caméra ultra-rapide capable de filmer jusqu'à 2000 images par seconde avec une résolution proche du micromètre.

1. Malgré l'utilisation de la caméra ultra-rapide, pourquoi ne peut-on pas obtenir d'images du film liquide en train de se rompre ?
2. L'onde circulaire créée est-elle longitudinale ou transversale ? Justifier.

Bien qu'éphémère, la vie d'une bulle n'en est pas moins riche en événements !

---

corrigé

---

La poussée d'Archimède qui s'exerce sur une bulle de volume V₀ dans la boisson :

direction verticale ; sens : vers le haut.

Expression littérale de sa valeur en fonction du volume V₀ de la bulle : poids du voume d'eau déplacé soit V₀r_e g.

---

Étude du mouvement d'une bulle en l'absence de force de frottement :
valeur du poids P₀ de la bulle : V₀ r_Co2 g ; valeur de la poussée d'Archimède F_A =V₀r_e g.

le rapport : P₀ / F_A : r_Co2 / r_e = 1,8 10^-3.

Le poids est environ 500 fois plus petit que la poussée d'Archimède : P₀ négligeable devant F_A.
Expression de la coordonnée a_z du vecteur accélération de la bulle en fonction des masses volumiques r_e et r_CO2 et de g :

La bulle n'est soumise qu'à la poussée d'Archimède, verticale, vers le haut, valeur : V₀r_e g.

La seconde loi de Newton s'écrit : m a_z = V₀r_e g avec m = V₀ r_Co2

a_z = r_e/ r_Co2 g .
Expression de la valeur de la vitesse de la bulle en fonction du temps :

La vitesse est une primitive de l'accélération ; de plus la vitesse initiale est nulle

v = a_z t = r_e/ r_Co2 g t
Durée t_s théoriquement nécessaire pour que la bulle atteigne la surface avec la vitesse v_s :

v_S=15 10^-2 m/s ; t_S= v_Sr_Co2 / (r_eg) = 15 10^-2 *1,8 / 10⁴ = 29 10^-6 s = 29 ms.
Cette valeur ne correspond pas aux observations de la vie quotidienne : le modèle proposé n'est pas valide.

---

Etude du mouvement de la bulle en présence d'une force de frottement :
Le liquide exerce sur la bulle une force de frottement, proportionnelle à sa vitesse, de valeur f = k v,, colinéaire et de sens contraire au vecteur vitesse. k est un coefficient qui dépend du rayon de la bulle et de la viscosité du fluide dans lequel elle se déplace.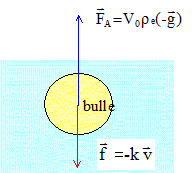

En appliquant la deuxième loi de Newton, l'équation différentielle qui régit l'évolution de la vitesse de la bulle s'écrit alors :

mdv/dt =V₀r_e g -kv avec m = V₀ r_Co2

V₀ r_Co2dv/dt + kv = V₀r_e g
dv/dt + kv/(r_CO2 V₀) =r_e /r_CO2 g
Expression littérale de la vitesse limite v_lim atteinte par la bulle :

Lorsque la vitesse limite est atteinte, le mouvement de la bulle est rectiligne uniforme : v_lim = constante et donc dv_lim/dt = 0.

l'équation différentielle s'écrit alors : kv_lim/(r_CO2 V₀) =r_e /r_CO2 g

v_lim =r_e g V₀ / k

L'application numérique donne v_lim voisin de 1 mm.s^-1. Pour parcourir une distance de 5 cm, hauteur du champagne dans un verre, cette bulle mettrait 50 s. Cette valeur ne correspond donc pas aux observations de la vie quotidienne : le modèle proposé n'est pas valide.

---

Pourquoi le volume de la bulle augmente si fortement lors de sa remontée ?

D'après le texte :" Il y a formation de bulles qui vont s'enrichir continûment en gaz au cours de leur remontée"

La quantité de matière n₀ de gaz présent dans la bulle augmente.

En assimilant le paz à un gaz parfait ( à température constante et à pression variant seulement de 2%), le volume de la bulle est proportionnel à la quantité de matière n₀ et en conséquence, ce volume augmente au cours de la remontée.

Influence de la variation du volume de la bulle sur chacune des forces qui s'exercent sur elle au cours de la remontée :
Durant l'ascension le poids de la bulle est toujours négligeable devant la poussée d'Archimède.

La poussée d'Archimède, de valeur V₀r_e g, est proportionnelle au volume de la bulle ; donc la poussée d'Archimède augmente avec V₀

Le coefficient k augmente avec le rayon de la bulle, donc la force de frotement de valeur kv, augmente avec V₀.

---

La bulle a maintenant gagné la surface et le film liquide qui constitue la partie émergée de la bulle s'amincit (figure 4.a) jusqu'à se rompre lorsque son épaisseur avoisine le micromètre. Le trou qui apparaît s'ouvre (figure 4.b) et la durée de disparition de la calotte sphérique n'est que de quelques dizaines de microsecondes.

Ces observations nécessitent l'utilisation d'une caméra ultra-rapide capable de filmer jusqu'à 2000 images par seconde avec une résolution proche du micromètre : la durée entre deux images est de l'ordre de 1/2000 = 5 10^-4 s = 500 ms, valeur très grande devant la durée de disparition de la calotte sphérique : on ne peut donc pas obtenir d'images du film liquide en train de se rompre.

L'onde circulaire créée est transversale : la direction de propagation de l'onde est perpendiculaire à la déformation du milieu liquide.

Le but de cet exercice est d'étudier les réactions nucléaires qui se produisent dans l'univers, notamment dans les étoiles, et qui engendrent la synthèse des éléments chimiques.
Masse d'un noyau d'hydrogène ou d'un proton : m_p = 1,67 10^-27 kg ; masse d'un positron (ou positon) : m_e ; célérité de la lumière dans le vide : c = 3,00 10⁸ m/s ; constante radioactive du "béryllium 8", l = 1 10¹⁶ s^-1 ; 1 eV = 1,60 10 ^-19 J ; constante de Planck : h= 6,63 10^-34 J.s

I- Les premiers éléments présents dans l'univers :

Selon le modèle du big-bang, quelques secondes après l'explosion originelle, les seuls éléments chimiques présents étaient l'hydrogène (90%), l'hélium et le lithium, ce dernier en quantité très faible. Les physiciens ont cherché à comprendre d'où provenaient les autres éléments existant dans l'univers.

1. Déterminer la composition des noyaux des atomes d'hélium ⁴₂He et ³₂He ainsi que celle de l'ion hélium ⁴₂He²⁺ .
2. La synthèse des éléments chimiques plus lourds se fait par des réactions nucléaires. Pourquoi cette synthèse ne peut-elle pas se faire par des réactions chimiques ?

II- Fusion de l'hydrogène :

Sous l'action de la force gravitationnelle les premiers éléments (hydrogène, hélium…) se rassemblent, formant des nuages gazeux en certains endroits de l'univers. Puis le nuage s'effondre sur lui-même et la température centrale atteint environ 107 K. A cette température démarre la première réaction de fusion de l'hydrogène dont le bilan peut s'écrire : 4 ¹₁H -->⁴₂He + 2 ⁰₁e . Une étoile est née.

1. En notant m_He la masse d'un noyau d' "hélium 4", écrire l'expression littérale de l'énergie |DE| libérée lors de cette réaction de fusion des 4 noyaux d'hydrogène. L'application numérique donne une valeur voisine de 4 10 ^-12 J.
2. Cas du Soleil :
   A sa naissance on peut estimer que le Soleil avait une masse d'environ M_S = 2 10³⁰ kg. Seul un dixième de cette masse est constituée d'hydrogène suffisamment chaud pour être le siège de réactions de fusion. On considère que l'essentiel de l'énergie produite vient de la réaction de fusion précédente. Montrer que l'énergie totale E_T pouvant être produite par ces réactions de fusion est voisine de 10⁴⁴ J.
   - Des physiciens ont mesuré la quantité d'énergie reçue par la Terre et en ont déduit l'énergie E_S libérée par le Soleil en une année : 10³⁴ J.an^-1 . En déduire la durée Dt nécessaire pour que le Soleil consomme toutes ses réserves d'hydrogène.

III- Un produit de la fusion de l'hélium :

D'autres réactions de nucléosynthèse peuvent se produire au cœur d'une étoile. Selon les modèles élaborés par les physiciens, l'accumulation par gravitation des noyaux d'hélium formés entraîne une contraction du cœur de l'étoile et une élévation de sa température. Lorsqu'elle atteint environ 10 ⁸ K, la fusion de l'hélium commence : ⁴₂He +⁴₂He -->⁸₄Be . Il se forme ainsi des noyaux de "béryllium 8" radioactifs de très courte durée de vie.

On s'intéresse à la radioactivité du "béryllium 8". Soit N(t) le nombre de noyaux de "béryllium 8" présents dans l'échantillon à l'instant de date t, et N₀ celui à l'instant de date t₀ = 0 s.

1. En utilisant la loi de décroissance radioactive, démontrer la relation entre la demi-vie t_1/2 et la constante radioactive l : l t_1/2 = ln2 .
2. Calculer le temps de demi-vie t_1/2 du "béryllium 8". Aide au calcul : ln2 = 0,7.
3. En déduire le rapport N(t₁)/N₀ à l'instant de date t₁ = 1,4 10 ^-16 s

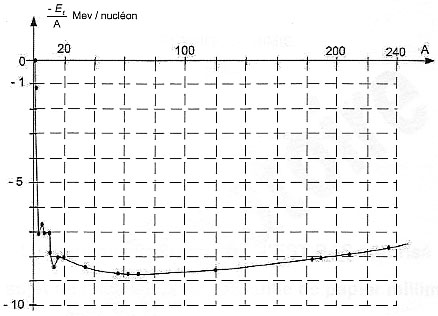
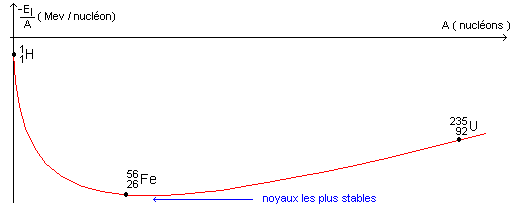
IV- Vers des éléments plus lourds :

Dans les étoiles de masse au moins 4 fois supérieure à celle du Soleil, d'autres éléments plus lourds peuvent ensuite être formés par fusion, par exemple le carbone ¹² C, l'oxygène ¹⁶O, le magnésium ²⁴Mg, le soufre ³²S (…) et le fer ⁵⁶Fe.

1. Donner l'expression littérale de l'énergie de liaison par nucléon E_l/A d'un noyau de fer ⁵⁶₂₆Fe , en fonction des masses du neutron m_n, du proton m_p, du noyau de "fer 56" m_Fe et de la célérité de la lumière dans le vide c.
2. Indiquer sur la courbe d'Aston représentée ci-dessous, le point correspondant à la position du noyau de "fer 56".
3. En s'aidant de la courbe précédente, dire où se situent les noyaux capables de libérer de l'énergie lors d'une réaction de fusion.

V- L'élément fer :

Dans certaines étoiles, à la fin de la période des fusions, une explosion se produit libérant de l'énergie. Des noyaux de fer ⁵⁶₂₆Fe sont dissociés et d'autres sont recréés par désintégration radioactive des noyaux de cobalt ⁵⁶₂₇Co . Les noyaux de fer, formés dans un état excité, émettent alors des rayonnements d'énergie bien déterminée, tels que le satellite SMM a pu en détecter en 1987 en observant une supernova dans le nuage de Magellan.

1. Lors de la désintégration radioactive du noyau de cobalt ⁵⁶₂₇Co il se forme, en plus du fer ⁵⁶₂₆Fe, une autre particule. Écrire l'équation de cette désintégration et nommer la particule formée.
2. L'un des rayonnements détectés a une énergie de 1238 keV. Quelle est l'origine de ce rayonnement émis par le fer ?
   - Ce rayonnement a une énergie bien déterminée. Que peut-on en déduire concernant les niveaux d'énergie du noyau de fer ?
   - Ce rayonnement est-il un rayonnement X ou g ?Justifier. On pourra s'aider de la gamme de longueur d'onde donnée ci-dessous.

 Aide aux calculs : 6,63 / (3*1,238 = 1,8 ; 1,238/(6,63*3) = 2,7 ; 3*6,63/1,238 = 16

1. Ce rayonnement est un rayonnement g d'après la gamme de longueur d'onde donnée.