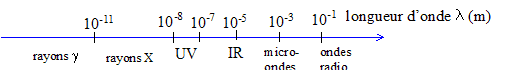|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||
|
|||
|
|
Le but de cet exercice est d'étudier les réactions nucléaires
qui se produisent dans l'univers, notamment dans les étoiles, et qui
engendrent la synthèse des éléments chimiques. I- Les premiers éléments présents dans l'univers : Selon le modèle du big-bang, quelques secondes après l'explosion originelle, les seuls éléments chimiques présents étaient l'hydrogène (90%), l'hélium et le lithium, ce dernier en quantité très faible. Les physiciens ont cherché à comprendre d'où provenaient les autres éléments existant dans l'univers.
II- Fusion de l'hydrogène : Sous l'action de la force gravitationnelle les premiers éléments (hydrogène, hélium…) se rassemblent, formant des nuages gazeux en certains endroits de l'univers. Puis le nuage s'effondre sur lui-même et la température centrale atteint environ 107 K. A cette température démarre la première réaction de fusion de l'hydrogène dont le bilan peut s'écrire : 4 11H -->42He + 2 01e . Une étoile est née.
III- Un produit de la fusion de l'hélium : D'autres réactions de nucléosynthèse peuvent se produire au cœur d'une étoile. Selon les modèles élaborés par les physiciens, l'accumulation par gravitation des noyaux d'hélium formés entraîne une contraction du cœur de l'étoile et une élévation de sa température. Lorsqu'elle atteint environ 10 8 K, la fusion de l'hélium commence : 42He +42He -->84Be . Il se forme ainsi des noyaux de "béryllium 8" radioactifs de très courte durée de vie. On s'intéresse à la radioactivité du "béryllium 8". Soit N(t) le nombre de noyaux de "béryllium 8" présents dans l'échantillon à l'instant de date t, et N0 celui à l'instant de date t0 = 0 s.
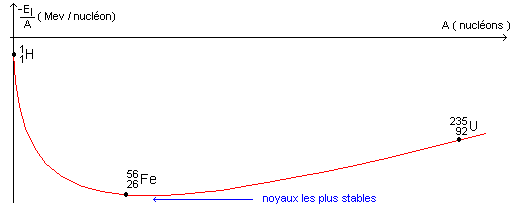
IV- Vers des éléments plus lourds : Dans les étoiles de masse au moins 4 fois supérieure à celle du Soleil, d'autres éléments plus lourds peuvent ensuite être formés par fusion, par exemple le carbone 12 C, l'oxygène 16O, le magnésium 24Mg, le soufre 32S (…) et le fer 56Fe.
V- L'élément fer : Dans certaines étoiles, à la fin de la période des fusions, une explosion se produit libérant de l'énergie. Des noyaux de fer 5626Fe sont dissociés et d'autres sont recréés par désintégration radioactive des noyaux de cobalt 5627Co . Les noyaux de fer, formés dans un état excité, émettent alors des rayonnements d'énergie bien déterminée, tels que le satellite SMM a pu en détecter en 1987 en observant une supernova dans le nuage de Magellan.
Aide aux calculs : 6,63 / (3*1,238 = 1,8 ; 1,238/(6,63*3) = 2,7 ; 3*6,63/1,238 = 16
corrigé Composition des noyaux des atomes d'hélium 42He et 32He ainsi que celle de l'ion hélium 42He2+ : 42He : 2 protons et 4-2 = 2 neutrons ; 32He : 2 protons et 3-2 = 1 neutron ; 42He2+ : 2 protons et 4-2 = 2 neutrons. La synthèse des éléments chimiques plus lourds se fait par des réactions nucléaires dans lesquelles la composition du noyau est modifiée. Une réaction chimique met en jeu quelques électrons externes, sans modifier la structure du noyau. 4 11H -->42He + 2 01e. Expression littérale de l'énergie |DE| libérée lors de cette réaction de fusion des 4 noyaux d'hydrogène. variation de masse |Dm|= mHe +2me -4 mP ; |DE| = |Dm| c² = (mHe +2me -4 mP) c² = 4 10 -12 J Cas du Soleil : Or la fusion de 4 noyaux d'hydrogène, soit d'une masse de 4*1,67 10-27 kg d'hydrogène, libère 4 10 -12 J. L'énergie totale ET pouvant être produite par ces réactions de fusion est voisine de : 4 10 -12 *2 1029 /(4*1,67
10-27) = 2 / 1,67 10 44 J =1,2 1044
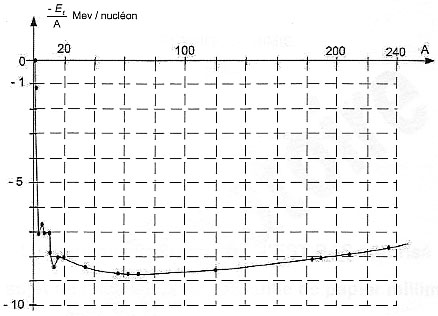
J. 1044 / 1034 = 1010 ans. 42He +42He -->84Be . On s'intéresse à la radioactivité du "béryllium 8". Soit N(t) le nombre de noyaux de "béryllium 8" présents dans l'échantillon à l'instant de date t, et N0 celui à l'instant de date t0 = 0 s. La loi de décroissance radioactive s'écrit : N(t) = N0 exp(-lt) ou encore ln (N0 / N(t) = lt. à t½ , N(t½) = ½N0 d'où : ln2 = l t1/2 . Calculer le temps de demi-vie t1/2 du "béryllium 8": t1/2 = ln2 / l avec la constante radioactive du "béryllium 8", l = 1 1016 s-1 t1/2 = 0,7 / 1016 = 7 10-17 s. Valeur du rapport N(t1)/N0 à l'instant de date t1 = 1,4 10 -16 s ln (N0 / N(t1) = lt1 = 1016 *1,4 10 -16 = 1,4 = 2*0,7 = ln2² d'où N0 / N(t1) = 4. Expression littérale de l'énergie de liaison par nucléon El/A d'un noyau de fer 5626Fe , en fonction des masses du neutron mn, du proton mp, du noyau de "fer 56" mFe et de la célérité de la lumière dans le vide c. On appelle énergie de liaison notée El d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos. 5626Fe compte 26 protons et 56-26 = 30 neutrons. El = |mFe- 26mp - 30mn | c² El/A =|mFe- 26mp - 30mn
| c² / 56. Lors de la désintégration radioactive du noyau de cobalt 5627Co il se forme, en plus du fer 5626Fe, une autre particule. L'équation de cette désintégration s'écrit : 5627Co --> 5626Fe* + 01e ( positrons) suivi de la désexitation du noyau de fer : 5626Fe* ---> 5626Fe + 00g. ( photon ) Ce rayonnement a une énergie bien déterminée : en conséquence les niveaux d'énergie du noyau de fer sont quantifiés. E= 1238 keV = 1,238 106 eV Exprimer cette énergie en joule : 1,238 106 *1,6 10-19 = 1,238*1,6 10-13 J De plus E = hn = hc/l soit l = hc/E = 6,63 10-34 * 3 108 /(1,238*1,6 10-13)= [6,63*3/1,238] / 1,6 10-13 =16/1,6 10-13 = 10-12 m
|
||
| |
|||
|
|