Aurélie 29/06/06

Le condensateur dans tous ces états : d'après bac Polynésie 09/03

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.


 

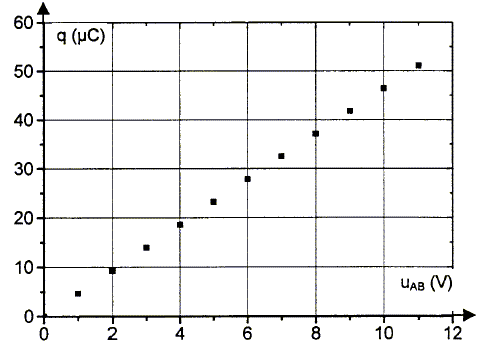
1ère partie :

On réalise le circuit ci- dessous constitué d'un générateur de courant, d'un condensateur, d'un ampèremètre, et d'un interrupteur. Le condensateur est préalablement déchargé, et à la date t = 0 s, on ferme l'interrupteur K. L'ampèremètre indique alors une valeur constante pour l'intensité I = 12 mA.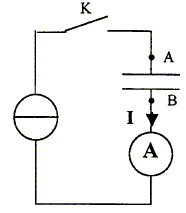

Un ordinateur muni d'une interface (non représenté) relève, à intervalles de temps réguliers, la tension uAB aux bornes du condensateur.
t (s)
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
uAB(V)
0,00
1,32
2,64
4,00
5,35
6,70
7,98
9,20
10,6

  1. Rappeler la relation permettant de calculer la charge q du condensateur en fonction de I. Calculer q à la date t = 3,0 s.
  2. On a représenté la courbe donnant la charge q du condensateur en fonction de uAB. Déterminer à partir de cette dernière, par une méthode que l'on explicitera, la valeur de la capacité C du condensateur.
  3. La valeur indiquée par le constructeur est C = 4,7 mF à 10 % près. La valeur obtenue est-elle en accord avec la tolérance du constructeur ?

2ème partie :

On étudie maintenant la charge et la décharge d'un condensateur à travers un conducteur ohmique. Pour cela, on réalise le montage suivant :

Le condensateur est initialement déchargé, et à la date t = 0 s, on bascule l'interrupteur en position 1.

Données : R = 2,2 kW ; C = 4,7 mF ; R' = 10 kW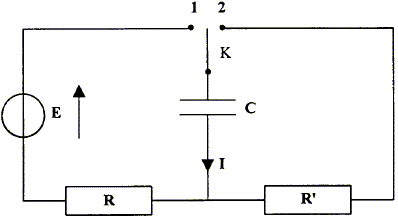

 

 

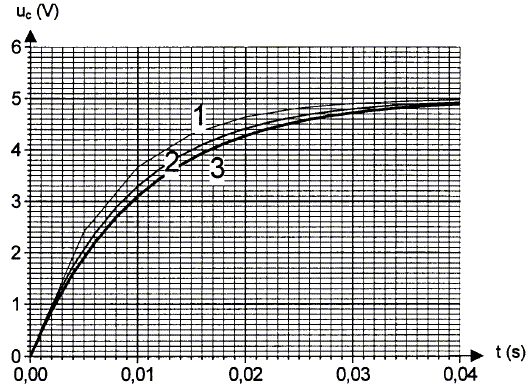
  1. Établir l'équation différentielle E = RC duC/dt + uC vérifiée par la tension uC aux bornes du condensateur pendant la phase de charge.
  2. La solution analytique de cette équation est de la forme : uC = A(1 - e xp(- a.t) ), compte tenu de la condition initiale relative à la charge du condensateur. En vérifiant que cette expression est solution de l'équation différentielle, identifier A et a en fonction de E, R, C.
  3. À partir graphe ci-dessous, déterminer la valeur E.
  4. La méthode d'Euler permet de calculer, pas à pas, les valeurs de uC et de duC/dt à intervalles de temps réguliers choisis Dt. Si D t est considéré comme suffisamment petit dans le cadre de l'expérience, on peut écrire : uC(t + Dt) = uC(t) +[duC/dt ]t D t . On choisit D t = 1 ms.
    - A l'aide de l'équation différentielle, déterminer la valeur initiale de la dérivée notée :[duC/dt ]0
    - En appliquant la méthode d'Euler, compléter le tableau suivant :
    t(ms)
    0
    1
    2
    3
    uC(t) (....)
    0


    [duC/dt ] (....)



  5. Sur le graphe, on a représenté trois courbes :
    Courbe n°1 : courbe obtenue par la méthode d'Euler avec un pas Dt = 5 ms,
    Courbe n°2 : courbe obtenue par la méthode d'Euler avec un pas D t = 2 ms,
    Courbe n°3 : représentation de la solution analytique de l'équation différentielle.
    - Quelle est l'influence du pas D t, utilisé dans la méthode d'Euler ?
    - Quels sont les avantages et les inconvénients d'avoir un D t très grand ou très petit ?
    - Qu'entend-on par "Si D t est considéré comme suffisamment petit dans le cadre de l'expérience" ?
  6. Définir la constante de temps du circuit. Déterminer sa valeur à partir du graphe par une méthode que l'on explicitera. En déduire une nouvelle valeur expérimentale de C et la comparer à la valeur nominale.
  7. On bascule alors l'inverseur en position 2. En justifiant, répondre par vrai ou faux aux affirmations suivantes :
    - La durée de la décharge du condensateur est supérieure à celle de la charge.
    - La constante de temps du circuit lors de la décharge est égale à (R + R')C.

corrigé

1ère partie :

Relation permettant de calculer la charge q du condensateur en fonction de I :

q= It avec Q en coulomb, I en ampère et t en seconde.

A la date t = 3,0 s, q = 0,012 *3,0 = 0,036 C.

Valeur de la capacité C du condensateur :

D'une part, la courbe q= f(uAB) est une droite de coefficient directeur 46 10-6 / 10 = 4,6 10-6 C V-1.

D'autre part q et uAB sont proportionnelles ; la constante de proportionalité est la capacité C

en conséquence C=4,6 10-6 F= 4,6 mF, en accord avec la valeur indiquée par le constructeur.

2ème partie :

Equation différentielle vérifiée par la tension uC aux bornes du condensateur pendant la phase de charge :

la loi d'additivité des tensions s'écrit: E = uR + uC (1)

Loi d'Ohm pour un résistor : uR = Ri avec i = dq/dt et q =Cuc soit i = Cduc/dt

uR = RC duc/dt

repport dans l'expression (1) d'où l'équation différentielle relative à uc : E = RCduc/dt + uc.

uc(t)= A(1-exp(-at) )

dériver uc par rapport au temps : duc/dt = Aa exp(-at)

repport dans l'équation différentielle :

E= RCAa exp(-at)+ A-Aexp(-at) = A + A(RCa-1)exp(-at)

vérifiée quel que soit t, si on identifie A à E et RCa-1=0 soit RCa=1 ; a=1/( RC).

Le graphe permet de déterminer la valeur E = 5,0 V.

Quand le condensateur est chargé, la tension à ses bornes vaut E : lire l'ordonnée de l'asymptote horizontale.

La méthode d'Euler

uC(t + Dt) = uC(t) +[duC/dt ]t D t . On choisit D t = 1 ms.
L'équation différentielle permet de déterminer la valeur initiale de la dérivée notée :[duC/dt ]0 :

à t=0 , le condensateur est déchargé , donc uC=0 ; l'équation différentielle s'écrit alors : E = RC[duC/dt ]0

soit [duC/dt ]0 = E/(RC) = 5 / (2,2 103 * 4,7 10-6) =4,8 102 V s-1.
Compléter le tableau suivant :
t(ms)
0
1
2
3
uC(t) (V)
0
0,48
0,92
1,3
[duC/dt ] (V s-1)
4,8 102
4,4 102
3,9 102
3,7 102
uC(1) = uC(0) +[duC/dt ]0 D t =0+4,8 102 * 10-3 =0,48 V .

E = RC[duC/dt ]1 +uC(1) soit [duC/dt ]1 =(E -uC(1) )/ RC = (5-0,48) / (2,2 103 * 4,7 10-6) =4,4 102 V s-1.

uC(2) = uC(1) +[duC/dt ]1 D t =0,48+4,4 102 * 10-3 =0,92 V .

[duC/dt ]2 =(E -uC(2) )/ RC = (5-0,92) / (2,2 103 * 4,7 10-6) =3,9 102 V s-1.

uC(3) = uC(2) +[duC/dt ]2 D t =0,92+3,9 102 * 10-3 =1,31 V .

[duC/dt ]3 =(E -uC(3) )/ RC = (5-1,31) / (2,2 103 * 4,7 10-6) =3,7 102 V s-1.

Sur le graphe, on a représenté trois courbes :
Courbe n°1 : courbe obtenue par la méthode d'Euler avec un pas Dt = 5 ms,
Courbe n°2 : courbe obtenue par la méthode d'Euler avec un pas D t = 2 ms,
Courbe n°3 : représentation de la solution analytique de l'équation différentielle.
Influence du pas D t, utilisé dans la méthode d'Euler :

Lorsque le pas est suffisamment petit, la courbe obtenue par la méthode d'Euler se superpose pratiquement avec la courbe analytique de l'équation différentielle. Mais un D t très petit entraîne un nombre important de calculs.

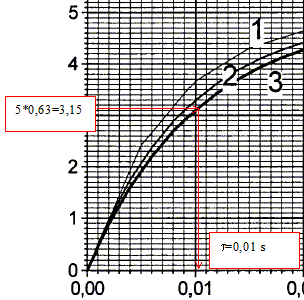
Par contre un pas assez grand, nécessite peu de calculs, mais la courbe obtenue s'éloigne d 'autant plus de la courbe analytique de l'équation différentielle.
"Si D t est considéré comme suffisamment petit dans le cadre de l'expérience" signifie :

t = RC = 2,2 103 * 4,7 10-6=0,010 s = 10 ms ; D t doit être de l'ordre de 0,2 t .

Constante de temps du circuit :t = RC

RC= 0,01 avec R = 22000 ohms soit C = 0,01 / 2200 = 4,5 10-6 F, en accord avec la valeur nominale, connue à 10 % près.

On bascule alors l'inverseur en position 2 : t' = R'C

" La constante de temps du circuit lors de la décharge est égale à (R + R')C. " est donc faux.

R' est égale à environ 5 R, donc t' voisin 5 t :

or, la durée de la charge ( ou de la décharge )vaut environ cinq fois la constante de temps.
"La durée de la décharge du condensateur est supérieure à celle de la charge" est donc vrai.



retour -menu