|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
On soumet à un flux de neutrons lents un échantillon d'argent ne contenant que des atomes d'argent 107. Un noyau d'argent 107 capte un neutron et il se forme un noyau d'argent 108. Le noyau d'argent 108 est radioactif. Il se désintègre suivant plusieurs processus compétitifs dont la radioactivité b - et la radioactivité b+. Donnée: extrait de la classification périodique fournissant les symboles des éléments et leur numéro atomique Rh : Z = 45; Pd : Z = 46 ; Ag : Z = 47 ; Cd : Z = 48 ; In :Z = 49 I- Capture d'un neutron :
II- Désintégration du noyau d'argent 108 :
III- Activité d'un échantillon de noyaux d'argent 108 : On considère un échantillon contenant N0 noyaux d'argent 108 à l'instant de date t = 0 s. Soit N, le nombre de noyaux restant à l'instant de date t.
IV- Demi-vie radioactive de l'argent 108 : On se propose de déterminer expérimentalement la demi-vie de l'argent 108. On s'inspire des résultats théoriques de la question 3 et on mesure le nombre n1 de désintégrations obtenues pendant la durée D t = 0,50 s. Cette mesure se répète toutes les 20 s. Les résultats sont rassemblés dans le tableau ci-dessous.
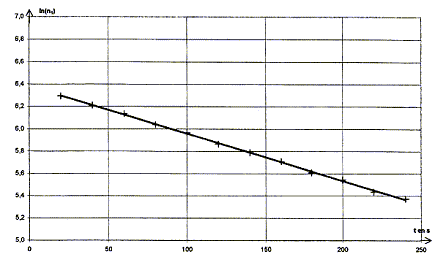
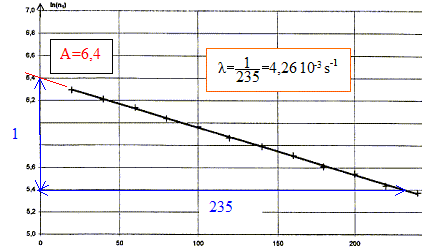
Capture d'un neutron : équation de la réaction de capture d'un neutron par un noyau d'argent 107 : 10747Ag + 10n = 10847Ag conservation du nombre de nucléons : 107+1 = 108 conservation de la charge : 47+0=47 Désintégration du noyau d'argent 108 : Les particules émises au cours des radioactivités b - et b+ sont respectivement un électron 0-1e et un positon 01e. équations correspondant à chacune des transformations radioactives pour l'argent 108 : 10847Ag = AZX + 0-1e la conservation du nombre de nucléon impose A= 108 ; la conservation de la charge conduit à : Z=48, élément cadmium Cd 10847Ag = AZX + 01e la conservation du nombre de nucléon impose A= 108 ; la conservation de la charge conduit à : Z=46, élément palladium Pd Activité d'un échantillon de noyaux d'argent 108 : On considère un échantillon contenant N0 noyaux d'argent 108 à l'instant de date t = 0 s. Soit N, le nombre de noyaux restant à l'instant de date t. la demi-vie radioactive t1/2 est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés. l t1/2 =ln2 ; ln2 étant sans dimension, en conséquence l est l'inverse d'un temps : [l]= T-1. l s'exprime en s-1. Expression de n1 en fonction de Dt, N0, t et l : d'une part A = -dN/dt et N= N0 exp(-lt) d'où : A= N0 lexp(-lt) = l N d'autre part : A = n1 / Dt en conséquence : n1 / Dt = N0 lexp(-lt) soit n1 = Dt N0 l exp(-lt) ln(n1) = ln(Dt N0 l) - lt Demi-vie radioactive de l'argent 108 : ln(n1) = ln(Dt N0 l) - lt : ln(Dt N0 l) est une constante ; l est également une constante positive ( -l négatif) : donc ln(n1) = A+Bt, fonction affine décroissante: La représentation graphique est en accord avec la relation ln(n1) = ln(Dt N0 l) - lt
ln(Dt N0 l) =A = 6,4 avec Dt = 0,5 s Dt N0 l = e6,4 ; N0 = e6,4 /(Dt l ) = e6,4 /(0,5*4,26 10-3)=2,8 105 noyaux. Or l t1/2 = ln2 soit t1/2 =ln2 / l = ln2 / 4,26 10-3 = 163 s.
|
|||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||
|
|