Aurélie 20/06/06

Evolution d'un système chimique, systèmes libre et forcé dans une automobile, radioactivité : à propos des noyaux d'argent.
d'après bac S Asie 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.


. .
.
.


Evolution d'un système chimique

Données: pKa des couples acide / base : Acide méthanoïque HCOOH(aq) / ion méthanoate HCOO -(aq) : pKa1 = 3,8

Acide benzoïque C6H5COOH (aq) / ion benzoate C6H5 COO -(aq) : pKa2 = 4,2

I- Étude de solutions aqueuses d'acide méthanoïque et d'acide benzoïque de même concentration :

On dispose de solutions aqueuses d'acide méthanoïque et d'acide benzoïque de même concentration molaire en soluté apporté c = 1,0 10- 2 mol/L. La mesure du pH d'un volume V = 10 mL de chaque solution fournit les résultats suivants : - solution aqueuse d'acide méthanoïque : pH1 = 2,9 ; - solution aqueuse d'acide benzoïque : pH2 = 3,1.

  1. La réaction de l'acide méthanoïque avec l'eau. Écrire 1'équation de cette réaction.
    -Calculer son avancement final, son avancement maximal ; en déduire son taux d'avancement final. On pourra s'aider d'un tableau descriptif de l'évolution du système chimique.
    Conclure sur le caractère total ou non de la transformation chimique mettant en jeu la réaction de l'acide méthanoïque avec l'eau.
  2. À partir de la comparaison des valeurs des pH des solutions aqueuses d'acide méthanoïque et benzoïque, dire pour quel acide la réaction avec l'eau est la plus avancée.

II- Évolution d'un système chimique :

Soit la réaction chimique suivante : HCOOH (aq) + C6H5 COO -(aq) = HCOO -(aq) + C6H5COOH (aq)

  1. Exprimer la constante d'équilibre de cette réaction puis calculer sa valeur.
  2. On dispose de solutions aqueuses d'acide méthanoïque et de benzoate de sodium de même concentration molaire en soluté apporté c et de solutions aqueuses d'acide benzoïque et de méthanoate de sodium de même concentration molaire en soluté apporté c '. On admettra que, dans leurs solutions aqueuses respectives : [HCOOH (aq)] = c ; [C6H5 COO -(aq)] = c ; [C6H5COOH (aq)] = c' ; [HCOO -(aq) ] = c'.
    On mélange des volumes V = 10,0 mL égaux des quatre solutions ci-dessus. Les concentrations molaires en soluté apporté c et c' ont les valeurs suivantes : c = 1,0 10-2 mol/L et c' = 5,0 10-3 mol/L. Calculer le quotient de réaction dans l'état initial dans ce cas précis. Dans quel sens va évoluer le système chimique ?
    Donnée : les réactions sur l'eau des ions benzoate et méthanoate sont peu avancées.
    - En maintenant V = 10,0 mL et c = 1,0 10-2 mol/L, quelle valeur faudrait-il donner à c' pour que le système soit en équilibre ?
corrigé
Étude de solutions aqueuses d'acide méthanoïque et d'acide benzoïque de même concentration :

Equation de la réaction de l'acide méthanoïque avec l'eau :

HCOOH (aq) + H2O = HCOO -(aq) +H3O+(aq)

L'avancement maximal vaut : xmax = Vc = 10-2*10-2 = 1,0 10-4 mol.

L'avancement final vaut : xfin = V 10-pH1 = 10-2 *10-2,9 = 1,3 10-5 mol.

Le taux d'avancement final vaut t =xfin / xmax =1,3 10-5 / 10-4 =0,13

je conclus : le taux d'avancement final étant inférieur à 1, la transformation chimique mettant en jeu la réaction de l'acide méthanoïque avec l'eau est donc limitée.

pour quel acide la réaction avec l'eau est-elle la plus avancée ?

Le taux d'avancement final s'exprime par : t = xfin / xmax = V 10-pH /(Vc) = 10-pH / c

D'une part les concentrations des deux solutions sont identiques, d'autre part le pH de la solution d'acide benzoïque est supérieur au pH de la solution d'acide méthanoïque ; de plus 10-pH est une fonction décroissante du pH : en conséquence la solution qui a le plus petit pH( l'acide méthanoïque) correspond à l'acide pour lequel la réaction avec l'eau est la plus avancée.

Évolution d'un système chimique :

Soit la réaction chimique suivante : HCOOH (aq) + C6H5 COO -(aq) = HCOO -(aq) + C6H5COOH (aq)

Expression de la constante d'équilibre de cette réaction : K= [HCOO -][C6H5COOH]/ ([C6H5 COO -][HCOOH]) (1)

d'une part : HCOOH (aq) + H2O = HCOO -(aq) +H3O+(aq) ; Ka1 = [HCOO -][H3O+] / [HCOOH]) (2)

d'autre part : C6H5COOH (aq) + H2O = C6H5 COO - (aq) +H3O+(aq) ; Ka2 = [C6H5 COO -][H3O+] / [C6H5COOH]) (3)

(2) divisé par (3) donne (1) soit K= Ka1 / Ka2 = 10-3,8 / 10-4,2 = 100,4 = 2,5.

quotient de réaction dans l'état initial :

Qr i= [HCOO -]i[C6H5COOH]i / ([C6H5 COO -]i [HCOOH]i )

avec [HCOO -]i = [C6H5COOH]i = 0,25 c' ( en tenant compte de la dilution lors du mélange)

et [C6H5 COO -]i = [HCOOH]i = 0,25 c

Qr i=c'²/c² = (5,0 10-3 / 1,0 10-2 )² = 0,5² = 0,25.

Qr i<K, le critère d'évolution spontané, indique une évolution dans le sens direct, de la gauche vers la droite.

valeur de c' pour que le système soit en équilibre :

si Qr i = K , le système est à l'équilibre

soit c'²/c² =2,5 d'où c'² =2,5 c² ; c'=2,5½ c = 1,6 10-2 mol/L.


systèmes libre et forcé dans une automobile ( 6,5 points)

Les parties 1 et 2 de cet exercice sont indépendantes

I- La suspension : les amortisseurs : (4 pts)

La suspension d'une automobile permet d'atténuer les oscillations verticales, inconfortables et dangereuses pour les passagers, se produisant lors du passage dans un trou ou sur un obstacle. Elle se compose au niveau de chaque roue d'un ressort et d'un amortisseur (généralement à huile).

Pour étudier ce système, l'automobile est modélisée par un solide de masse m, de centre d'inertie G reposant sur un ressort vertical de constante de raideur k. Le repérage des positions y du centre d'inertie de l'automobile se fait selon un axe vertical Oy orienté vers le haut ; l'origine O est choisie à la position d'équilibre G0 du centre d'inertie du solide. Les amortisseurs engendrent globalement une force de frottement opposée au vecteur vitesse du solide et proportionnelle à sa valeur ; le coefficient de proportionnalité h s'appelle coefficient d'amortissement.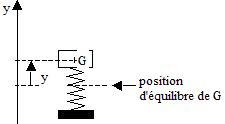

 

  1. Quelle est l'expression correcte de la période propre T0 de l'oscillateur ? La justifier par une analyse dimensionnelle :
    T0 = 2p(k/m)½ ; T0 = 2p(m/k)½ ; T0 = 2p(km)½ .
  2. On considère deux automobiles A1 et A2, assimilables chacune à un solide de même masse m reposant sur un ressort vertical de constante de raideur k = 6,0 105 N/m. La figure ci-après présente les courbes y(t) des positions du centre d'inertie G du solide modélisant chaque automobile lors du passage sur une bosse.

    - Les oscillations sont-elles libres ou forcées ?
    - Donner les noms des régimes associés aux courbes 1 et 2.
    - L'une des courbes présente une pseudo-période. Déterminer graphiquement sa valeur.
    - En admettant que la valeur de la pseudo-période est très voisine de celle de la période propre, calculer la masse m commune de chaque automobile.
    - Les allures différentes des courbes sont dues au coefficient d'amortissement h. Quelle courbe correspond à la plus grande valeur de h ? Justifier la réponse. Quelle automobile possède la meilleure suspension ?

  3. De nombreux garages possèdent un dispositif permettant de tester la suspension d'une automobile : il impose à la roue testée une excitation verticale périodique dont on peut faire varier la fréquence f. Le dispositif permet d'enregistrer l'amplitude des oscillations de la caisse en fonction de la fréquence. Les courbes ci-dessous ont été obtenues lors de deux tests réalisés sur deux amortisseurs.

    - À quel type d'oscillations sont soumis les amortisseurs lors de ces tests ? Justifier la réponse en citant un verbe dans la description du dispositif servant au test.
    - L'amplitude des oscillations passe par un maximum pour une fréquence voisine d'une fréquence caractéristique de l'amortisseur. Laquelle ? Comment s'appelle alors ce phénomène ?
    - Quel est l'amortisseur qui assure le plus de confort aux passagers ?

II- L'alimentation électrique: l'accumulateur au plomb :

La batterie de démarrage d'une automobile est constituée par l'association, en série, de plusieurs éléments d'accumulateurs au plomb. Un élément d'accumulateur comprend deux électrodes : l'une est en plomb métal Pb(s), l'autre est recouverte de dioxyde de plomb PbO2(s). Elles sont immergées dans une solution aqueuse d'acide sulfurique. Les deux couples oxydant / réducteur impliqués dans le fonctionnement de cet accumulateur sont : PbO2(s) / Pb2+ (aq) et Pb2+ (aq) / Pb(s).

  1. Lors de la décharge, l'accumulateur joue le rôle de générateur. L'oxydant PbO2(s) et le réducteur Pb(s) réagissent spontanément l'un sur l'autre. En écrivant les équations aux électrodes, montrer que l'équation de la réaction s'écrit alors : PbO2(s) + 4 H+ (aq) + Pb(s) = 2 Pb2+ (aq) + 2 H2O( l)
    - Identifier l'électrode négative de ce générateur en justifiant la réponse.
    - Le fonctionnement du démarreur nécessite un courant d'intensité 200 A. Le conducteur actionne le démarreur pendant 1,0 s ; quelle est la masse de plomb Pb(s) consommée ? masse molaire atomique du plomb: 207,2 g.mol-1 ; faraday (1 F) = 96500 C/mol ;
    constante d'Avogadro NA = 6,02 1023 mol-1 ; charge électrique élémentaire e = 1,6 10-19 C.
  2. Lors de la charge, l'accumulateur joue le rôle d'électrolyseur. Un générateur de charge, de force électromotrice supérieure à celle de l'accumulateur est branché en opposition avec celui-ci : la borne positive du générateur est reliée à l'électrode positive de l'accumulateur, la borne négative à l'électrode

    négative. Le sens du courant est imposé par le générateur de charge.

    - Écrire l'équation de la réaction chimique se produisant lors de la charge.
    - La transformation est-elle spontanée ou forcée

corrigé
La suspension : les amortisseurs :

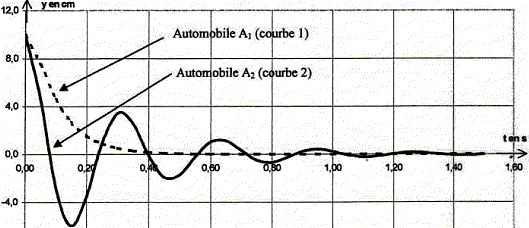
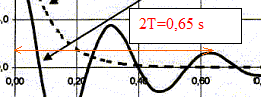
Expression correcte de la période propre T0 de l'oscillateur : analyse dimensionnelle
T0 = 2p(k/m)½ ; T0 = 2p(m/k)½ ; T0 = 2p(km)½ .

2p est sans dimension ; masse : [m]= M ; [T0]= T

D'une part, la valeur de la tension d'un ressort est proportionnelle à sa déformation x ; le coefficient de proportionalité est la raideur k : en conséquence k est égal à une force divisée par une longueur . k = F/x

D'autre part, la seconde loi de Newton indique qu'une force est égale à une masse multipliée par une accélération : F= ma

De plus une accélération est une longueur divisée par un temps élevé au carré .

en conséquence, la dimension de k est : [k]= [ma/x]= MLT-2 L-1 = MT -2

dimension de k/m : [k/m]= MT-2 M-1 = T-2 ; soit [k/m]½=T-1 ;

je conclus : T0 = 2p(k/m)½ ne convient pas.

dimension de m/k : [m/k]= M-1 T 2 M = T2 ; soit [m/k]½=T ;

je conclus : T0 = 2p(m/k)½ convient.

dimension de km : [m/k]= MT -2 M =M2 T -2; soit [mk]½=MT-1 ;

je conclus : T0 = 2p(mk)½ ne convient pas.

Les oscillations sont libres : au delà de la bosse, le ressort n'est pas sollicité par un excitateur
A la courbe 1 correspond un régime apériodique ( on n'observe pas d'oscillation) ; à la courbe 2 on associe un régime pseudopériodique ( l'amplitude des oscillation diminue au cours du temps).
Détermination graphique de la pseudo-période :

T voisin de 0,325 s soit 0,32 s.
masse m commune de chaque automobile :

d'une part T voisin T0 = 0,33 s et d'autre part :T0 = 2p(m/k)½ soit T²0 = 4p² m/k : m = kT²0 / (4p² )

m = 6,0 105 * 0,325² / (4*3,14²) =1,6 103 kg.

Les allures différentes des courbes sont dues au coefficient d'amortissement h : l'amortissement est d'autant plus grand que le coefficient d'amortisement h est grand : donc la courbe 1 correspond à la plus grande valeur de h.

Une bonne suspension correspond à un coefficient d'amortissement grand : les passagers ne doivent pas être soumis à des oscillations à chaque passage de bosse.

"il impose à la roue testée une excitation verticale " : en conséquence, lors de ces tests les amortisseurs sont soumis à des oscillations forcées.

L'amplitude des oscillations passe par un maximum pour une fréquence voisine de la fréquence propre, caractéristique de l'amortisseur : ce phénomène porte le nom de résonance.
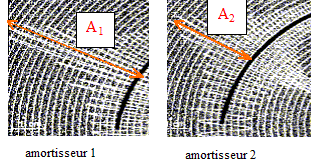
L'amortisseur qui assure le plus de confort aux passagers doit donner des oscillations dont l'amplitude est la plus faible possible à la résonance :

A2 <A1, donc l'amortisseur 2 assure le meilleur confort.

L'alimentation électrique: l'accumulateur au plomb :

Lors de la décharge, l'accumulateur joue le rôle de générateur.

couple :PbO2(s) / Pb2+ (aq) ; l'oxydant PbO2(s) se réduit : PbO2(s) + 4 H+ (aq) + 2e- = Pb2+ (aq)+ 2 H2O( l) ( 1) .

couple : Pb2+ (aq) / Pb(s) ; le réducteur Pb(s) s'oxyde : Pb(s) = Pb2+ (aq)+ 2e- ( 2) .

Des électrons porteurs d'une charge négative sont libérés lors de cette oxydation, en conséquence cette électrode de plomb constitue la borne négative de ce générateur.

( 1) + ( 2) conduisent à l'équation de la réaction : PbO2(s) + 4 H+ (aq) + Pb(s) = 2 Pb2+ (aq) + 2 H2O( l)

masse de plomb Pb(s) consommée :

Le fonctionnement du démarreur nécessite un courant d'intensité 200 A. Le conducteur actionne le démarreur pendant 1,0 s ;

en conséquence la quantité d'électricité Q mise en jeu est : Q=It = 200*1 = 200 C.

Or Q= n(e-) F : avec F, le faraday : 1F = NA e et n(e-) : quantité de matière (mol) d'électrons

d'où : n(e-) = Q/(NA e)

De plus : Pb(s) = Pb2+ (aq)+ 2e- d'où : n(e-) = 2 n(Pb) soit n(Pb) = ½ n(e-)

enfin m(Pb) = n(Pb) M(Pb)

par suite la masse de plomb disparue s'exprime par : m(Pb) = ½QM(Pb) / (NA e)

m(Pb) = 0,5*200 *207,2 / ( 6,02 1023 *1,6 10-19)=0,21 g.

Lors de la charge, l'accumulateur joue le rôle d'électrolyseur : le sens du courant est imposé par le générateur de charge.

en conséquence la transformation est forcée, l'accumulateur reçoit de l'énergie électrique de la part du générateur de charge.

L'équation de la réaction chimique se produisant lors de la charge est l'inverse de la réaction chimique de décharge.

2 Pb2+ (aq) + 2 H2O( l) = PbO2(s) + 4 H+ (aq) + Pb(s)

radioactivité : à propos des noyaux (5,5 points)

On soumet à un flux de neutrons lents un échantillon d'argent ne contenant que des atomes d'argent 107. Un noyau d'argent 107 capte un neutron et il se forme un noyau d'argent 108. Le noyau d'argent 108 est radioactif. Il se désintègre suivant plusieurs processus compétitifs dont la radioactivité b - et la radioactivité b+.

Donnée: extrait de la classification périodique fournissant les symboles des éléments et leur numéro atomique

Rh : Z = 45; Pd : Z = 46 ; Ag : Z = 47 ; Cd : Z = 48 ; In :Z = 49 

I- Capture d'un neutron :

  1. Rappeler les deux lois de conservation qui permettent d'écrire l'équation d'une réaction nucléaire.
  2. Écrire l'équation de la réaction de capture d'un neutron par un noyau d'argent 107. 

II- Désintégration du noyau d'argent 108 :

  1. Rappeler la nature des particules émises au cours des radioactivités b - et b+. Écrire leur symbole.
  2. Ecrire les équations correspondant à chacune des transformations radioactives pour l'argent 108.

III- Activité d'un échantillon de noyaux d'argent 108 :

On considère un échantillon contenant N0 noyaux d'argent 108 à l'instant de date t = 0 s. Soit N, le nombre de noyaux restant à l'instant de date t.

  1. Rappeler l'expression de N en fonction de N0, de t et de la constante radioactive l.
  2. Donner la définition de la demi-vie radioactive t1/2.
  3. La relation entre la demi-vie radioactive t1/2 et la constante radioactive l est l t1/2 =ln2 . Le symbole ln représente le logarithme népérien. Quelle est l'unité de l ?
  4. L'activité à l'instant t d'un échantillon est définie par la relation A = -dN/dt . Elle représente le nombre de désintégrations qui ont lieu par seconde. On détermine l'activité en mesurant le nombre n1 de désintégrations qui se produisent pendant une durée Dt très petite devant la demi-vie radioactive t1/2. On a alors A = n1 / Dt. Montrer que l'activité peut aussi s'exprimer par A = l N.
    - Exprimer n1 en fonction de Dt, N0, t et l.
    - En déduire l'expression de ln(n1) en fonction de Dt, N0, t et l.

IV- Demi-vie radioactive de l'argent 108 :

On se propose de déterminer expérimentalement la demi-vie de l'argent 108. On s'inspire des résultats théoriques de la question 3 et on mesure le nombre n1 de désintégrations obtenues pendant la durée D t = 0,50 s. Cette mesure se répète toutes les 20 s. Les résultats sont rassemblés dans le tableau ci-dessous.

 
t(s)
20
40
60
80
100
120
140
160
180
200
220
240
n1
542
498
462
419
390
353
327
301
273
256
230
216
Grâce à un tableur, il est possible de tracer le graphe représentant l'évolution de ln(n1) en fonction du temps. Le graphe est donné ci-après.

  1. La représentation graphique est-elle en accord avec la relation trouvée précédemment ?
  2. En utilisant le graphe, déterminer l et N0.
  3. En déduire t1/2.

 

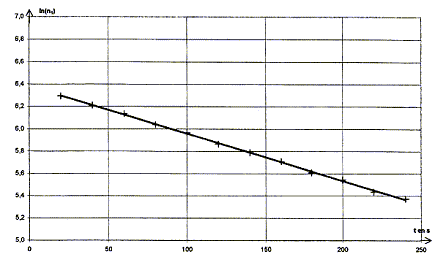
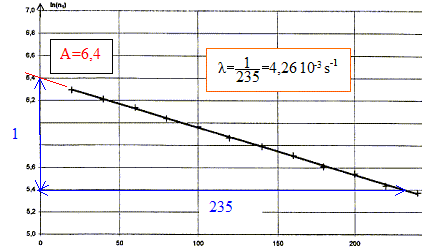
corrigé
Capture d'un neutron :

équation de la réaction de capture d'un neutron par un noyau d'argent 107 :

10747Ag + 10n =  10847Ag

conservation du nombre de nucléons : 107+1 = 108

conservation de la charge : 47+0=47

Désintégration du noyau d'argent 108 :

Les particules émises au cours des radioactivités b - et b+ sont respectivement un électron 0-1e et un positon 01e.

équations correspondant à chacune des transformations radioactives pour l'argent 108 :

 10847Ag = AZX + 0-1e

la conservation du nombre de nucléon impose A= 108 ; la conservation de la charge conduit à : Z=48, élément cadmium Cd

10847Ag = AZX + 01e

la conservation du nombre de nucléon impose A= 108 ; la conservation de la charge conduit à : Z=46, élément palladium Pd

Activité d'un échantillon de noyaux d'argent 108 :

On considère un échantillon contenant N0 noyaux d'argent 108 à l'instant de date t = 0 s. Soit N, le nombre de noyaux restant à l'instant de date t.

expression de N en fonction de N0 de t et de la constante radioactive l : N= N0 exp(-lt)

la demi-vie radioactive t1/2 est la durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés.

l t1/2 =ln2 ; ln2 étant sans dimension, en conséquence l est l'inverse d'un temps : [l]= T-1. l s'exprime en s-1.

Expression de n1 en fonction de Dt, N0, t et l :

d'une part A = -dN/dt et N= N0 exp(-lt) d'où : A= N0 lexp(-lt) = l N

d'autre part : A = n1 / Dt

en conséquence : n1 / Dt = N0 lexp(-lt) soit n1 = Dt N0 l exp(-lt)

ln(n1) = ln(Dt N0 l) - lt

Demi-vie radioactive de l'argent 108 :

ln(n1) = ln(Dt N0 l) - lt :

ln(Dt N0 l) est une constante ; l est également une constante positive ( -l négatif) : donc ln(n1) = A+Bt, fonction affine décroissante:

La représentation graphique est en accord avec la relation ln(n1) = ln(Dt N0 l) - lt

ln(Dt N0 l) =A = 6,4 avec Dt = 0,5 s

Dt N0 l = e6,4 ; N0 = e6,4 /(Dt l ) = e6,4 /(0,5*4,26 10-3)=2,8 105 noyaux.

Or l t1/2 = ln2 soit t1/2 =ln2 / l = ln2 / 4,26 10-3 = 163 s.

 



retour -menu