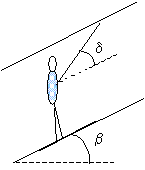
Un skieur de masse m= 80 kg (avec son équipement), est tiré par la perche d’un téléski ; celle-ci fait un angle 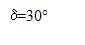avec la piste.
La piste est un plan incliné formant un angle 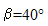avec le plan horizontal.
Le skieur est en mouvement de translation rectiligne et uniforme.
Les frottements sont équivalents à une force unique , parallèle à la ligne de plus grande pente , de valeur F=50 N. g = 9,8 m/s²
Déterminer la valeur T de la force exercée par la perche sur le skieur et la valeur R de la réaction normale de la piste sur les skis.





: piste, supposé galiléen
: axe Ox parallèle à la piste orienté vers le haut du plan incliné et axe Oy perpendiculaire à la piste
système étudié : skieur supposé ponctuel
bilan des forces : vertical, vers le bas, de valeur
réaction normale à la piste, vers le haut, de valeur R
force de frottements parallèle à la piste vers le bas, de valeur F
la force due à la perche suivant la perche, vers le haut, de norme T
D'après la première loi de Newton ( ou principe d') le mouvement étant rectiligne uniforme, alors la vectorielle des force est .
Ecrire cette relation vectorielle suivant chaque axe :


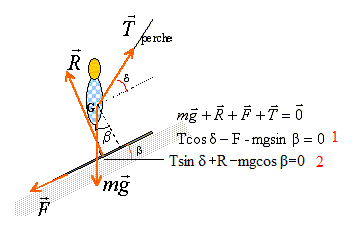
la relation (1) s'écrit : T =50+80*9,8 sin 40 / (cos30) = 640 .
la relation (2) s'écrit : R= 80*9,8*cos40-640*sin30 = 280 N.