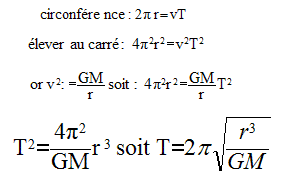On considère un satellite S décrivant, dans le repère géocentrique, une orbite circulaire centrée sur le centre de la Terre.
On admet que le satellite, assimilé à un point matériel de masse m, est soumis uniquement à la force gravitationnelle de la Terre.
On étudie son mouvement dans le référentiel géocentrique.
a) Montrer que son mouvement est uniforme.
b) Etablir l'expression de sa vitesse v et de sa période de révolution T, en fonction de la constante de gravitation universelle G, de la masse de la Terre M, du rayon de la Terre R et de son altitude h ( on posera R+h = r)

Le système étudié est le satellite,dans le référentiel géocentrique, considéré comme pendant la durée de l'étude.
Il est seulement soumis à la force de gravitation de la Terre :
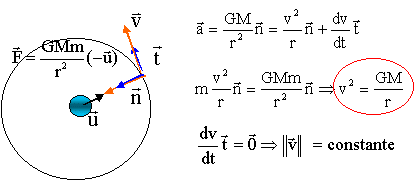
où n est un vecteur unitaire radial .
La force est perpendiculaire à chaque instant au vecteur vitesse, donc son travail est .
L'énergie cinétique est donc .
La valeur de la vitesse est constante : le mouvement est .

L'accélération est à la trajectoire
D'où la valeur de la vitesse : 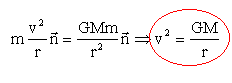

La période notée T ( ) est la durée nécessaire pour décrire une circonférence ou un de rayon r () à la vitesse de valeur constante (m/s ) :