Une masse est libre de se déplacer sans frottement sur un rail horizontal. On l'écarte de sa position d'équilibre, on la libère sans vitesse initiale.
a) Schématiser les forces qui agissent sur la masse m. Le point O repère l'abscisse du centre de gravité G à la position d'équilibre du système. Dans cette position le ressort n'est ni étiré ni comprimé.
b) En utilisant la deuxième loi de Newton, démontrer que l'équation différentielle du mouvement relative à l'abscisse x du centre de gravité G d à l'instant t s'écrit : d²x/dt²+w0²x=0 où w0² =k/m
Etablir cette équation dans un référentiel terrestre supposé galiléen.
c) Montrer que l'expression x(t) = A.sin(w0 t+j ) est solution de cette équation différentielle.
A l'instant initial t = 0 s, l'oscillateur possède une amplitude x0 = 2 cm ( ressort comprimé) et une vitesse v0 = 0. Déterminer les constantes A et j qui correspondent à ces conditions initiales.
d) Exprimer la période propre T0 des oscillations de l'oscillateur en fonction de k et m.
e) Exprimer l'énergie cinétique Ec de S en fonction du temps . Tracer l'allure de Ec = Ec(t).
Sans calcul, ajouter, sur le graphe précédent, les allures des variations au cours du temps de l'énergie mécanique de S, Em = Em (t), et celles de son énergie potentielle élastique Ep = Ep (t). Justifier.
e) Schématiser les énergies en fonction de x.
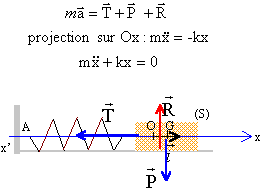
la masse m est soumise à :
- son poids, vertical, vers le bas, valeur mg
- l'action du support, vertical vers le haut, au poids.
- la tension du ressort, horizontale, valeur T= .

x(t) = A.sin(w0 t+j )
par rapport au temps : = dx/dt = A w0 cos(w0 t+j )
dériver à nouveau par rapport au temps : = d²x/dt² = -A w0² sin(w0 t+j ) = - A k/m sin(w0 t+j )
repport dans l' différentielle : - Ak/m sin(w0 t+j ) + Ak/m sin(w0 t+j ) =0 est vérifiée quel que soit t
donc x(t) = A.sin(w0 t+j ) est solution de cette équation différentielle.
les constantes A et j qui correspondent à ces conditions initiales :
initiale [dx/dt]t=0 =0 soit = A w0 cos(j ) = 0 donc j = pi/2 ou bien j = pi/2.
x(t=0) = m soit -0,02 = A.sin(j )
A amplitude égale à 0,02 m, donc j = -pi/2 .
période propre T0 des oscillations de l'oscillateur en fonction de k et m :
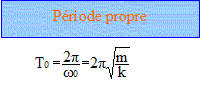 | 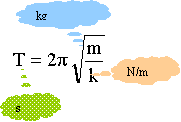 |
énergie cinétique : Ec=
.
énergie potentielle élastique Ep=
.
énergie mécanique =E=
des énergies cinétique et potentielle.
En absence de frottement, l'énergie mécanique se
.
Une masse est libre de se déplacer sans frottement sur un rail horizontal. Après avoir écarté la masse de sa position d'équilibre, on la libère sans vitesse initiale.
a) Représenter sur un schéma les forces agissant sur la masse m. Le point O donne l'abscisse du centre de gravité G à la position d'équilibre du système. Dans cette position le ressort n'est ni étiré ni comprimé.
b) En utilisant la deuxième loi de Newton, démontrer que l'équation différentielle du mouvement relative à l'abscisse x du centre de gravité G du mobile à l'instant t s'écrit : d²x/dt²+w0²x=0 où w0² =k/m
On établira cette équation dans le référentiel terrestre supposé galiléen.
c) Montrer que l'expression x(t) = A.sin(w0 t+j ) est solution de cette équation différentielle.
On suppose qu'à l'instant initial t = 0 s, l'oscillateur possède une amplitude x0 = 2 cm ( ressort comprimé) et une vitesse v0 = 0. Déterminer les constantes A et j qui correspondent à ces conditions initiales.
d) Exprimer la période propre T0 des oscillations de l'oscillateur en fonction de k et m.
e) Etablir l'expression de l'énergie cinétique Ec de S en fonction du temps . Tracer l'allure de Ec = Ec(t).
Sans calcul, ajouter, sur le graphe précédent, les allures des variations au cours du temps de l'énergie mécanique de S, Em = Em (t), et celles de son énergie potentielle élastique Ep = Ep (t). Justifier.
e) Schématiser les énergies en fonction de x.

la masse m est soumise à :
- son poids, vertical, vers le bas, valeur mg
- l'action du support, vertical vers le haut, au poids.
- la tension du ressort, horizontale, valeur T= .

x(t) = A.sin(w0 t+j )
par rapport au temps : = dx/dt = A w0 cos(w0 t+j )
dériver à nouveau par rapport au temps : = d²x/dt² = -A w0² sin(w0 t+j ) = - A k/m sin(w0 t+j )
repport dans l' différentielle : - Ak/m sin(w0 t+j ) + Ak/m sin(w0 t+j ) =0 est vérifiée quel que soit t
donc x(t) = A.sin(w0 t+j ) est solution de cette équation différentielle.
les constantes A et j qui correspondent à ces conditions initiales :
initiale [dx/dt]t=0 =0 soit = A w0 cos(j ) = 0 donc j = pi/2 ou bien j = pi/2.
x(t=0) = m soit -0,02 = A.sin(j )
A amplitude égale à 0,02 m, donc j = -pi/2 .
période propre T0 des oscillations de l'oscillateur en fonction de k et m :
énergie cinétique : Ec=.
énergie potentielle élastique Ep=.
énergie mécanique =E= des énergies cinétique et potentielle.
En absence de frottement, l'énergie mécanique se .