(Newton 1867) entre les masses.
1) Quel est le référentiel le mieux adapté à l’étude du mouvement de la Lune autour de la Terre ? Justifier
2) Donner les caractéristiques (faire un schéma) de la force de gravitation exercée par la Terre sur la Lune, de la force de gravitation exercée par la Lune sur la Terre.
3) Préciser la signification de chaque grandeur et indiquer les unités. Calculer leur valeur commune.
Masse de la terre M= 6,0 10 exposant 24 kg ( notée 6,0 10^ 24)
Masse de la Lune m = 7,4 ´ 10 eposant2 2 kg notée 7,4 10^22.
Constante de gravitation universelle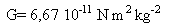 
Distance entre les centres de la Terre et de la Lune d = 3,8 ´ 10 exposant 5 km ( notée 3,8 10^ 5 km)
Le référentiel est le plus adapté pour décrire simplement le mouvement de la lune autour de la terre.
Un référentiel terrestre ne convient pas, car l’étude serait compliquée par la rotation de la terre sur elle-même.
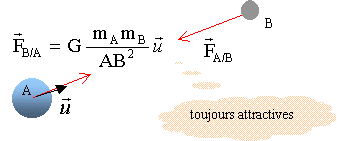
Deux corps A et B de masses respectives M et m, exprimées en , séparés d'une distance d=AB, exprimée en , exercent l'un sur l'autre des forces opposées , importantes dans l'infiniment , négligeables dans l'infiniment .
Ces forces ont pour direction la droite passant par les des 2 planètes.
La valeur commune de ces forces est proportionnelle aux et inversement proportionnelle au de la distance qui les séparent. La constante de proportionalité est la constante de gravitation, notée G.
Exprimer la distance d=AB en mètre : 3,8 10^ 5 km = 3,8 10^ m.
(Coulomb 1785) entre les charges.
Une charge ponctuelle Q = 10 nC est placée au sommet A d'un carré ABCD de 2 cm de côté.
En C, sommet diagonalement opposé à A, est placée une charge ponctuelle q = 5 nC.
Constante d'interaction électrostatique :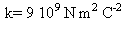
1) Donner les caractéristiques (faire un schéma) des forces électriques exercées entre les charges
2) Préciser la signification de chaque grandeur et indiquer les unités. Calculer leur valeur commune.
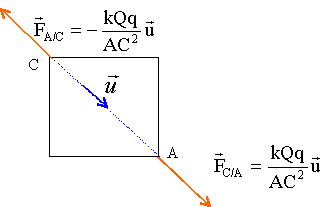
Ces forces ont pour direction la droite () joignant les charges ponctuelles.
Les charges de même signe se repoussent : les forces sont .
Deux corps A et B de charges respectives Q et q, exprimée en (C), séparés d'une distance d, exprimée en , exercent l'un sur l'autre des forces opposées ou répulsives, importantes dans l'infiniment petit, négligeables dans l'infiniment grand.
La valeur commune de ces forces est proportionnelle aux et inversement proportionnelle au de la distance qui les séparent.
diagonale du carrée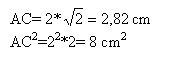 
AC² = 8 cm² = 8 10 exposant m².
Charges Q= 10 nC = 10 10 exposant C ; q= 5 10 exposant C
