

La dimension d'une grandeur G se note entre crochets : [G].
Pour une masse : [G] = M, la grandeur G a la dimension d'une masse ; G est
à une masse.
La relation [G] = M est l'
aux dimensions de la grandeur G.
[G] =1 : la grandeur est dite sans dimension ou de dimension 1.
Pour un angle, on obtient 1 mais il y a quand même une unité, le radian.
Une équation est dite
si ses deux membres ont la même dimension.

On ne peut
( ou soustraire) que des termes ayant la même dimension.
La dimension du produit de deux grandeurs est le produit des dimensions de chaque grandeurs : [AB] = [
][
].
La dimension de
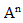
est :
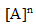
où n est un nombre sans dimension.
Dans les expressions : sin(u), cos(u), tan(u), ln(u), log(u) et
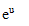
, la grandeur u est sans dimension.

Vérifier qu'une formule est homogène. Exemple, la période d'un pendule :
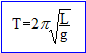
L est une
: [L]= L
g est une
, c'est à dire une longueur divisée par un temps au carré :
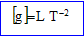
Le nombre pi est sans dimension.
L'équation au dimensions du second membre s'écrit :
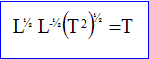
L'expression de la période est homogène car les deux termes de l'équation ont la même dimension, celle d'un temps.