On se propose d’étudier la diffraction obtenue avec un faisceau laser passant à travers un trou circulaire.
On mesure, pour 4 ouvertures circulaires de diamètres a différents, le rayon r de la tache centrale de diffraction obtenue sur un écran situé à la distance D = 4,50 m du trou.

a( m)	4,90 10 ^ -4	6,20 10^ -4	8,20 10 ^ -4	1,23 10^ -3
r( m)	7,5 10^ -3	6,0 10^ -3	4,5 10^ -3	3,0 10^-3
1/ a ( m-1)

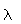
Le laser émet un faisceau de lumière monochromatique de longueur d’onde dans le vide = 670 nm.
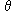
L’écart angulaire entre le centre de la tache centrale de diffraction et la première extinction a pour expression : .
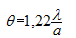
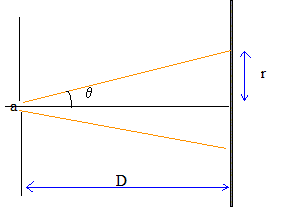
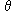
1. Faites un schéma de la situation en faisant apparaître les grandeurs : , a, r et D.

2.On propose 4 expressions pour le diamètre de l’ouverture circulaire :

a) Montrez, par analyse dimensionnelle, que l’une des expressions est manifestement fausse.
b) En analysant les résultats expérimentaux, trouvez la seule expression qui convient.
c) Retrouvez cette expression en utilisant le schéma de la question 1.

La dimension a de la fente étant une , les expressions correctes doivent avoir la dimensions d’une longueur : c’est le cas des relations 1, 2 et 4 qui sont donc .
L’expression 3 est sans dimension et n’est donc pas homogène.
L’analyse des résultats expérimentaux montre que r est une fonction décroissante de a ( r et a varient en sens ) : seule l’expression 1 correspond à cette propriété.


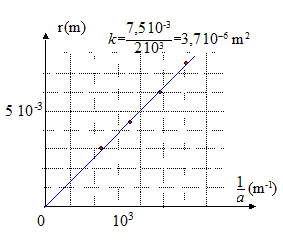
3. a) Après avoir complété la troisième ligne du tableau des résultats expérimentaux , tracez, le graphe représentatif de la fonction r= f(1/a).
b) A partir de ce graphe, retrouvez la valeur de .

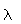
a( m)	4,90 10 ^ -4	6,20 10^ -4	8,20 10 ^ -4	1,23 10^ -3
r( m)	7,5 10^ -3	6,0 10^ -3	4,5 10^ -3	3,0 10^-3
1/ a ( m-1)	2,04 10^ 3	1,61 10^3	1,22 10^3	813

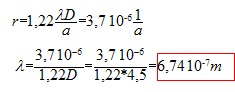
longueur d'onde : nm.