On considère un dipôle RLC série comprenant un résistor de résistance R= 10 ohms, une bobine d'inductance L et de résistance r <R et un condensateur parfait de capacité C. Ce dipôle est alimenté par une tension alternative sinusoïdale 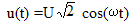
Le rapport de la tension efficace Ur aux bornes du résistor à la tension efficace U aux bornes du dipôle AB est noté a=Ur/U.
1) Pour la fréquence f=fo, la valeur de "a" passe par un maximum ao. Expliquer ce résultat, en déduire la valeur de r, effectuer l'application numérique avec ao=0,700.
Tension efficace aux bornes du résistor Ur= ( I étant l'intensité efficace)
Tension efficace aux bornes du dipôle : U= ZI. ( Z : du dipôle)
A la fréquence f=fo, les effets du condensateur compensent ceux de la bobine. L'impédance du dipôle est , égale à R+r.
En conséquence le rapport Ur/U est maximal, égal à : ao=R/(R+r)
R+r= R/ao soit r = R(1/ao-1) = 10(1/0,7-1)= ohms.
2) La valeur précédente fo est égale à 1,000 kHz.
a) Pour des fréquences très inférieures à fo, on constate que la valeur de "a" est pratiquement proportionnelle à f. Quel est alors l'élément déterminant pour le fonctionnement du circuit ? Justifier
b) Pour des fréquences très supérieures à fo, on constate que la valeur de "a" est pratiquement proportionnelle à 1/f. Quel est alors l'élément déterminant pour le fonctionnement du circuit ? Justifier
c) Pour f=10 Hz, on constate que a=1,25.10^-4. En déduire les valeurs numériques de C et L. Calculer numériquement "a" pour f=1,0.10^5Hz
Impédance Z du dipôle RLC : 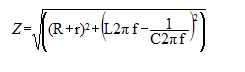
- Aux faibles fréquences, le terme"1/(2pi f C)", relatif au , est bien au terme "L2pi f" relatif à la bobine.
Or "a" = R/Z : si de plus (R+r) << "1/(2pi f C)" alors "a" est proportionnel à la fréquence.
Le est l'élément déterminant si f<
- A f >>fo, c'est le terme "L2pi f" qui l'emporte sur le terme "1/(2pi f C)"
Or "a" = R/Z : si de plus (R+r) << "L2pi f" alors "a" est proportionnel à l'inverse de la fréquence.
La est l'élément déterminant si f>>fo.
- f= 10 Hz : 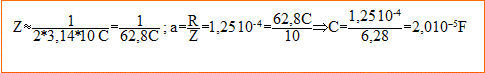
- fréquence propre du dipole :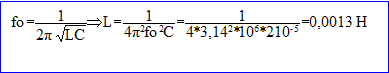
- f= 100 kHz : 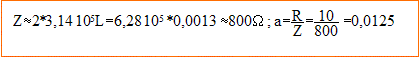
3) Déterminer à 980Hz et à 1020 Hz le déphasage, en degrés, de la tension aux bornes de R, par rapport à la tension totale u.
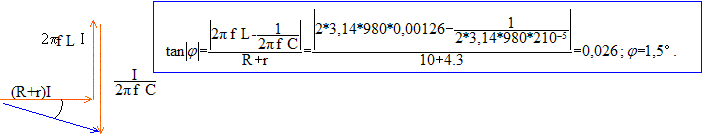
A f=980 Hz, l'intensité, donc la tension aux bornes du résistor R est en sur la tension aux bornes du dipole.
A f=1020 Hz, l'intensité, donc la tension aux bornes du résistor R est en de 1,1° sur la tension aux bornes du dipole.