L’ammoniac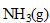 
est formé par réaction entre le diazote et le dihydrogène selon l’équation chimique suivante :
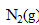+ 3 
= 2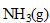
On mélange, à 400 °C, sous une pression totale de 100 bar, 8,4 mol de diazote et 21 mol de dihydrogène, tous deux à l’état gazeux. Les gaz seront considérés comme parfaits. La pression et la température sont maintenues constantes pendant la réaction.
Données : 1 bar = 10^5 Pa ; R = 8,31 J.mol-1.K-1.
1. Quel est le volume initial du système chimique ?
température T= +400 = 673 K.
pression = *10^5 = 10^ 7 Pa.
nombre total de moles : n= 8,4 + 21 = mol
V= nRT/P = 29,4*8,31*673 / 10^7 = 1,65 10^-2 mètre cube = L
2. Quelle est la composition du système chimique en fonction de l'avancement X, à la date t.
A l’équilibre, un quart de la quantité initiale de diazote a disparu. Donner la composition du système chimique, l’avancement et le volume obtenu à la fin de la réaction.
| avancement (mol) | 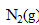| +3 | =2 |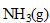
| initial | 0 | 8,4 | 21 | 0 |
| en cours | X | 8,4-X | 21-3X | 2X |
| équilibre | Xf | 8,4-Xf | 21-3Xf | 2Xf |
A l’équilibre, un quart de la quantité initiale de diazote a disparu : Xf= 8,4/4 = 2,1 mol
n(N2)=
mol
n(H2) =21-3*2,1=
mol
n(NH3)= 2*2,1 =
mol
nombre total de mol : 25,2 mol
Volume final obtenu ( T et P étant constants, quantité de matière et volume sont
) :
V = 16,5*25,2 / 29,4=
L.
3. On appelle rendement, le rapport de la quantité de matière obtenue et de la quantité de matière thèorique si la réaction était totale. Calculer le rendement en ammoniac.
Si la réaction est totale :
si N2 en
: 8,4-Xmax=0 soit Xmax=8,4 mol
Si H2 en défaut : 21-3Xmax =0 soit Xmax= 7 mol
On retient la plus
valeur.
r = Xf / Xmax = 2,1 / 7 = 0,3. Le rendement est de
%.
L.
3. On appelle rendement r en un produit de la réaction, le rapport de la quantité de matière obtenue et de la quantité de matière que l’on obtiendrait si la réaction était totale. Calculer le rendement en ammoniac.
Si la réaction est totale :
si N2 en : 8,4-Xmax=0 soit Xmax=8,4 mol
Si H2 en défaut : 21-3Xmax =0 soit Xmax= 7 mol
On retient la plus valeur.
r = Xf / Xmax = 2,1 / 7 = 0,3. Le rendement est de %.