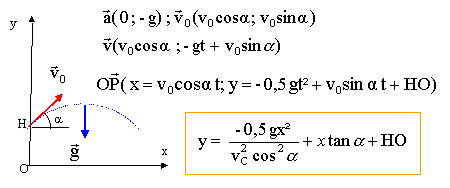Aurélie 04/05

Associations de résistors ;

Haut parleur ; Projectile ; eau de Javel ; spectrophotométrie ; équilibre chimique

physique 1 h ; chimie 0,5 h ; d'après concours kiné Rennes 2005

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


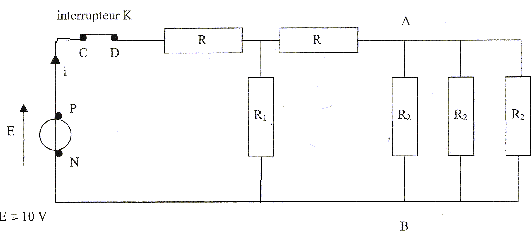
Toute réponse sera justifiée par un raisonnement scientifique ou par un calcul approprié sauf pour l'exercice IV

Associations de résistors (6 pts)

 

Pour chaque réponse donner l'expression littérale, puis la valeur de la grandeur rechechée.

  1. On prend R= 10 W , R1=2R et R2 = 3 R.
    - Quelle est la résistance équivalente au circuit ?
    - Déterminer l'intensité du courant i.
    - Déterminer les tensions UAB et UDC.
  2. Dans cette partie R= R1=R2.
    - Quelle doit être la valeur de R pour que l'intensité du courant soit i= 0,40 A ?
    - Quelle est alors l'énergie dissipée par effet joule par R en 1 min ?
    - Quelle est l'énergie fournie au circuit par le générateur pendant ce même laps de temps ?
    - On ouvre l'interrupteur K, déterminer les tensions UAB et UDC.
corrigé
entre A et B, trois résistors identiques en dérivation : résistance équivalente R4= R2/3 = R

puis R et R4 en série, équivalents à :R5=R+R4 = 2R

puis R1 et R5 en parallèle, équivalent à : R6= R1R5/(R1+R5)=2R*2R/(4R) = R

puis R en série avec R6 : Réqui = R+R6 = 2R= 20 ohms.

I= E/Réqui = 10/20 = 0,5 A.

I=I1+I2 avec R1I2 = (R+R4)I1 ; 2RI2 = (R+R)I1 ; I1=I2 = ½I

UAB= R4I1 = R½I= 10*0,22 = 2,5 V ; UDC=0 , interrrupteur fermé.

de même en faisant R=R1=R2 :

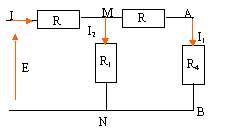
R4=R/3 ; R5=R+R/3=4R/3 ; R6 = R1R5/(R1+R5)=4 R/7 ; Réqui = R+4R/7 = 11R/7.

E= Réqui I =11R/7 I soit R= 7E/(11I) = 70 / (11*0,4) = 15,9 W.

Energie fournie par le générateur : E(V) I(A) t(s) = 10*0,4*60 = 240 J.

Energie dissipée dans les résistors :

dans R situé à gauche de M : RI² t = 15,9*0,4²*60 = 152,6 J

dans le résistor R situé entre M et A : RI1²t avec : R1I2 = (R+R4)I1 ; RI2 = (R+R/3)I1 ; I1+I2 = I

I1 = 3I/7 = 0,171 A ; I2 = 7/3 I1 = 0,229 A

RI1²t =15,9*0,171²*60 = 27,8 J

dans le résistor situé entre M et N : RI2²t = 15,9 * 0,229²*60 = 50 J

dans R4 : R4I²1 t = 5,3*0,171²*60 = 9,4 J.

interrupteur K ouvert : UAB=0 et UDC= - E = -10 V.

Haut parleur : (5 points)

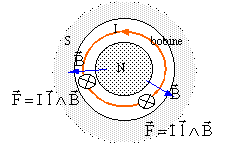
Un haut parleur est posé sur une table horizontale, dôme vers le haut.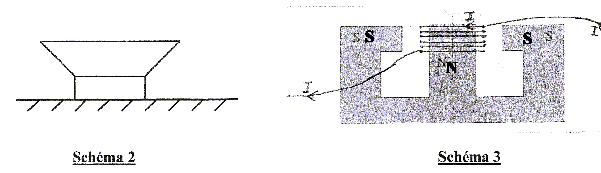

 

  1. La bobine du haut parleur est traversée par un courant I constant. Le champ magnétique est radial, c'est à dire dirigé suivant le rayon de la bobine, et orienté du pôle Nord vers le pôle Sud de l'aimant.
    - Quel nom donne-t-on à la force électromagnétique alors subie par la bobine.
    - Faire un schéma représentant une vue de dessus du schéma3 et représenter le vecteur champ et le vecteur force électromagnétique, en quatre points différents.
    - La bobine est solidaire de la membrane du haut parleur. Quel a été le mouvement de cette dernière quand l'intensité du courant est passer de 0 à I ,et avant d'atteindre sa position d'équilibre ?
  2. On se trouve maintenant dans le cas de figure où la membrane du haut parleur a un mouvement ascendant. On désire mesurer la force électromagnétique qui s'exerce sur cette membrane. Pour ce faire on place une masse marquée m sur le dôme de manière à ce que la membrane reprenne la position qu'elle avait lorsque I=0.. Les résulatats des mesures sont rassemblés ci-dessous :
    m(g)
    50
    100
    150
    200
    250
    I(A)
    0,1
    0,2
    0,35
    0,39
    0,5
    - Montrer que ces résultats sont compatibles avec l'expression de la force électromagnétique.
    - Quelle est la valeur de cette force s'il faut poser une masse m= 120 g ?

 

corrigé
La bobine susceptible de se déplacer, traversée par un courant I, placée dans un champ magnétique, est soumise aux forces de Laplace.

Le forces de Laplace sont verticales, vers le bas.( vers le haut, si I change de sens)

A l'équilibre la membrane ( solidaire de la bobine et du cône) est soumise à la force de Laplace, verticale, vers le haut , valeur n B I l ( n : nombre de spires de la bobine) et au poids des masses marquées , vertical, vers le bas, valeur mg.

Ces forces sont opposées et ont m^me valeur :

mg = n B I l

la masse et l'intensité sont proportionnelles.

m(g)
50
100
150
200
250
I(A)
0,1
0,2
0,35
0,39
0,5
m/I( g/A)
500
500
429
513
500
écart relatif : (513-429)/500 = 0,17 ( 17%)

l'une des mesures est fausses ; l'affirmation ci-dessus est bien vérifiée.

si m = 0,12 kg alors F= mg = 0,12*9,8 = 1,17 N.


Projectile :( 4pts)

Une bille d'acier que l'on suppose ponctuelle, est lancée vers le haut à t=0 avec une vitesse v0 faisant un angle a avec l'horizontale d'une hauteur H= 6,0 m au dessus du sol. On néglige les frottements avec l'air.

Le repère est tel que l'axe Ox est horizontal et se trouve au niveau du sol, l'axe Oy est vertical vers le haut. A t=0 , les coordonnées de la bille sont (0 ; 6).

  1. Etablir les équations horaires du mouvement.
  2. La bille atteint le sommet de la trajectoire en F tel que (xF= 1,0 ; yF= 6,4) à t= 0,29 s. En déduire les valeurs de v0 et a.
  3. La bille touche le sol au point B.
    - Quelle sera la vitesse vB lorsq'elle arrive en ce point ?
    - Calculer OB.
  4. Une voiture commandée que l'on supposera ponctuelle, se déplace d'un mouvement rectiligne et uniforme avec une vitesse V)= 5 m/s, selon l'axe Ox et de la gauche vers la droite.
    - Où doit-elle se trouver à t=0, si on désire que les deux objets ( voiture et bille) arrivent en même temps en B ?
    g = 9,8 m/s²)

corrigé

Au sommet S la vitesse est horizontale : -gt + v0sin a=0 soit t = v0sina/ g.

xS= v0² sina cosa / g = v0² sin(2a)/(2g)

yS= -½ g v0² sin²a/g² + v0² sin²a/g + HO = ½v0² sin²a/g + HO

(yS-HO)/xS= ½tan a soit tan a = 2*(6,4-6)/1 = 0,8 ; a = 38,66 °.

v0² = 2gxS/ sin(2a) = 2*9,8*1/sin 77,3) = 20,1 soit v0 = 4,48 m/s.

entre le point H et le point B l'énergie mécanique se conserve car seul le poids travaille

en H : ½mv²0 + mgOH ; en B : ½mv²B ( O : origine de l'énergie potentielle de pesanteur)

v²B = v²0 + 2gOH = 4,48²+2*9,8*6 = 137,7 ; vB= 11,73 m/s.

au sol : xB= v0sin a t = 4,48 cos 38,66 t = 3,5 t.

yB=0 = -4,9 t² + 4,48*sin 38,66 t + 6 ; -4,9 t² + 2,8 t+6 = 0

résoudre ; on trouve t= 1,428 s.

par suite xB= 3,5*1,428 = 5 m.

équation horaire du mouvement de la voiture : x= Vt + x0 = 5t + x0 ;

à t = 1,428 s, x= xB=5 m ; x0 = x-Vt= 5-5*1,428 = -2,14 m ( à t=0, la voiture est 2,14 m à gauche de O).

couples redox : Cl2(g) Cl-(aq) ; ClO-(aq) / Cl2(g); H2O2/H2O ; I2/I-.

Vm= 22,4 L/mol ( C.N.T.P) ; Vm= 24 L/mol à 20°C sous 1 bar.
R= 8,31 S.I; masse atomique molaire (g/mol) H : 1 ; O : 16 ; Ca : 40,1 ; C : 12.

L'eau de javel : (2 pts) 

L'eau de javel est obtenue par l'action du dichlore gazeux sur une solution d'hydroxyde de sodium. Le principe actif de l'eau de Javel est l'ion hypochlorite ClO-(aq) qui est responsable de l'action décolorante sur les textiles.On caractérise la teneur en ion hypochlorite par le degré chlorométrique. : c'est le nombre de litres de dichlore mesuré dans les conditions normales de température et de pression, qui sont absorbés lors de la préparation de 1 L d'eau de Javel.

  1. Ecrire l'équation chimique de la réaction de préparation de l'eau de Javel.
    - Que peut-on dire du dichlore au cours de cette réaction.
  2. Un flacon d'eau de javel porte l'indication 12 ° chlorométrique. Calculer la concentration des ions hypochlorite de cette eau de javel.
corrigé
Cl2(g) + 2HO- = ClO- + Cl- + H2O

Le dichlore se dismute :

Cl2(g) + 2e- = 2Cl- réduction du dichlore

Cl2(g) + 4HO- = 2ClO-+ 2e- +2 H2O oxydation du dichlore

12°Ch, donc 12 L de dichlore dissous dans 1 L de solution

Qté de matière de dichlore (g) = volume (L) / volume molaire( L/mol) (CNTP) = 12 / 22,4 = 0,536 mol

soit [ClO-]= 0,536 mol/L.

Suivi spectrophotométrique d'une réaction : (4 pts)

 

En solution aqueuse le peroxyde d'hydrogène H2O2 réagit lentement avec l'ion iodure I-(aq). Le diiode en solutionprésente un maximum d'absorption vers lmax= 350 nm. A cette longueur d'onde une solution aqueuse de diiode de concentration [I2]=0,7 10-5 mol/L a une absorbance Al= 1,75. On rappelle que l'absorbance d'une solution est proportionnelle à sa concentration, loi de beer-Lambert. Dans la cuve du spectrophotomètre on mélange 3,0 mL de solution de iodure de potassium accidifié, de concentration [I-]=0,01 mol/L avec un volume de 0,5 mL d'une solution de peroxyde d'hydrogène, de concentration [H2O2]= 5 10-5 mol/L. On relève l'absorbance en fonction du temps :
t(min)
0
1
3
5
8
10
15
20
30
A
0
0,4
0,95
1,29
1,52
1,63
1,72
1,77
1,78

  1. Expliquer pourquoi cette réaction peut être suivie par spectrophotométrie.
  2. Quelle est la concentration maximale du diiode à t infini ?
  3. Quelle serait l'absorbance du milieu réactionnel à la date t infini ? Comparer ce résultat à l'absorbance obtenue à la date t= 30 min et conclure.
corrigé
Cette réaction peut être suivie par spectrophotométrie, car seul l'ion iodure présente une forte absorption à la longueur d'onde choisie.

H2O2 + 2e- +2H+= 2H2O réduction

2I- = I2 + 2e- oxydation

bilan : H2O2 +2I- +2H+ = I2 +2H2O

Qté de matière initiale d'ion iodure : volume (L) * concentration = 3 10-3 * 0,01 = 3 10-5 mol.

Qté de matière initiale de H2O2 : 0,5 10-3 * 5 10-5 = 2,5 10-8 mol (en défaut)

Qté maximale de matière I2 : 2,5 10-8 mol dans 3,5 mL ; [I2]max = 2,5 10-8 / 3,5 10-3 = 7,14 10-6 mol/L

Une solution aqueuse de diiode de concentration [I2]=0,7 10-5 mol/L a une absorbance Al= 1,75 :

Al= k [I2] avec k une constante égale à : 1,75 / 0,7 10-5 = 2,5 105 L mol-1.

Aoo= k [I2]max 2,5 105 *7,14 10-6 =1,785.

L'absorbance Aoo est pratiquement égale à l'absorbance mesurée à t = 30 min.

Donc la réaction est pratiquement terminée à t = 30 min.

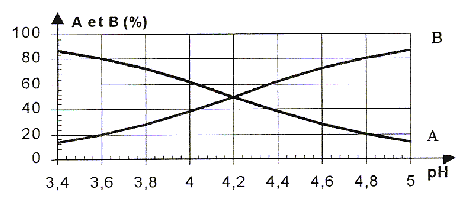
Evolution d'un équilibre chimique : (2 pts)

 

Ce diagramme permet de définir les domaines de prédominance ainsi que la distribution des espèces données C6H5-COOH ( noté A) et C6H5-COO- ( noté B) en solution aqueuse en fonction du pH de la solution. On étudie la transformation rapide associée à la réaction acido-basique à 25 °C

C6H5-COOH + H2O = C6H5-COO- + H3O+.

  1. On considère un volume V0= 100 mL d'une solution S0 d'acide benzoïque caractèrisée par pH= 3,6. Le système est-il en équilibre ? Justifier.
  2. On ajoute à cette solution une masse m de benzoate de sodium. Le système évolue vers un état d'équilibre dans lequel le rapport des concentrations est [B]/[A]=4,0. Déterminer le pH et montrer par le calcul que le système a atteint un état d'équilibre.

 

corrigé
C6H5-COOH + H2O = C6H5-COO- + H3O+ ou A + H2O = B +H3O+

Qr,i =[B]i[H3O+]i/[A]i avec[B]i/[A]i =0,2/0,8 = 0,25 ( lecture graphe à pH=3,6)

Qr,i =0,25 10-3,6 =6,27 10-5.

or la constante d'équilibre vaut : pKa= 4,2 soit Ka = 10-4,2 =6,3 10-5.( lecture graphe à l'intersection des courbes)

Qr,i = Ka, donc l'équilibre est atteint.

[B]/[A]=4,0 : lecture graphe pH= 4,8 ( soit B= 80% et A = 20%)

Qr =[B][H3O+]/[A] =4* 10-4,8 =6,34 10-5.

Qr = Ka, donc l'équilibre est atteint.


Un spéléologue fait de la chimie: (2 pts)

 

L'acéthylène C2H2 peut être fabriqué par action de l'eau sur le carbure de calcium CaC2(s). Il se forme également de l'hydroxyde de calcium Ca(OH)2 (s). L'acéthylène réagit avec le dioxygène de l'air avec formation de dioxyde de carbone et d'eau. Il se produit une flamme éclairante.

Un spéléoloque utilise une lampe à acéthylène qui consomme 10 L( volume mesuré à 20°C et sous 1,013 105 Pa) de ce gaz par heure de fonctionnement. Il désire disposer de 10 heures d'éclairage mais il souhaite être chargé au minimum. Calculer la masse de carbure de calcium et d'eau qu'il doit emporter.

 

corrigé
CaC2(s) + 2H2O = C2H2 +Ca(OH)2 (s).

Qté de matière acéthylène = volume (L) / volume molaire (L/mol) = 100 / 24 = 4,17 mol.

n(CaC2) =4,17 mol ; n(H2O) =2*4,17 = 8,34 mol

masse (g) = masse molaire (g/mol) * qté de matière (mol)

m((CaC2) =( 40,1+2*12) * 4,17 =267,3 g.

m(eau) = 18*8,34 =150,1 g.


retour -menu