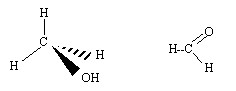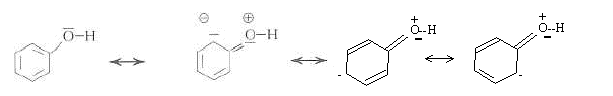|
physique : étude d'oscillateurs ; optique géométrique et ondulatoire d'après concours caplp2 1996 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||
| .
. |
||||
|
||||
|
|
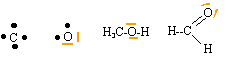
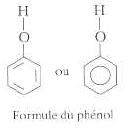
corrigé Structures électroniques de l'état fondamental de l'atome de carbone : 1s2, 2s2, 2p2 et de l'atome d'oxygène :1s2, 2s2, 2p4 . La valence d'un atome est égale au nombre de liaisons de covalence simples mises en oeuvre par un atome valence du carbone : 4 et de l'oxygène : 2 La valence est égale au nombre d'électrons externes célibataires. Dans le cas du carbone on observe une hybridation de type sp3 entre l'orbitale 2 s et les orbitales 2p représentations de Lewis des atomes de carbone et d'oxygène, des molécules de méthanol et de méthanal :
Les arrangements VSEPR autour des atomes de carbone AX4 ( structure tétraédrique) et d'oxygène AX2E2 ( forme en V) dans le méthanol, autour de l'atome de carbone AX3 ( plane triangulaire) dans le méthanal. Les molécules de méthanol et de méthanal en utilisant les conventions de Cram.
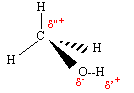
Le caractère polaire des liaisons C-O et
O-H dans la molécule de méthanol. Les électrons de la liaison covalente
sont plus proches de l'atome le plus électronégatif.
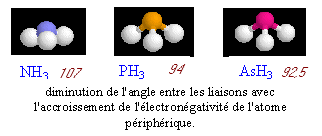
Le volume occupé par les doublets liants décroît lorsque la différence d'électronégativité des atomes liés augmente. Drainés vers l'atome le plus électronégatif, les électrons de liaison davantage confinés dans l'espace internucléaire se repoussent moins. La mesure de l'angle de liaison C-O-H dans la molécule de méthanol sera proche de 106°.
|
|||
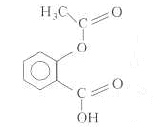
Formule brute : C9H8O4 ; M= 9*12+8*4*16 = 184 g/mol. Volume minimal de solution obtenu par dissolution complète d'un comprimé d'aspirine pur 0,5 g On peut dissoudre 3,3 g dans 1 L d'eau d'où : 0,5*1/3,3 = 0,152 L. Qté de matière aspirine dans 0,5 g = masse (g) / masse molaire (g/mol) = 0,5 / 184 = 2,72 10-3 mol Concentration molaire de la solution S : Qté de matière (mol) / volume de la solution (L) = 2,72 10-3 /0,151 =1,8 10-2 mol/L. Réaction entre cet acide et l'eau : AH + H2O= H3O+ + A- ; Ka = 3,2 10-4. la solution est électriquement neutre et HO- négligeable en milieu acide : [H3O+]=[A-] conservation de A :[A-] + [AH] = 1,8 10-2 mol/L ; [AH] + [H3O+] = 1,8 10-2 Ka = [H3O+][A-]/[AH] =3,2 10-4 ; [H3O+]² / (1,8 10-2 - [H3O+])=3,2 10-4 ; [H3O+]² = 3,2 10-4 (1,8 10-2 - [H3O+]) [H3O+]² +3,2 10-4 [H3O+]-3,2 10-4 *1,8 10-2=0 [H3O+] = 2,24 10-3 ; pH= 2,65.
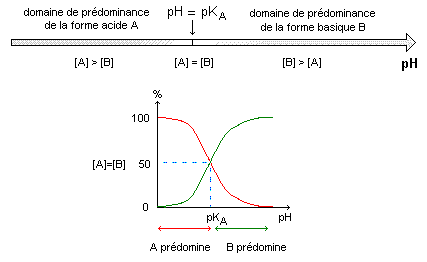
La forme prédominante de l'aspirine à pH= 5, inférieur à pKa est la forme acide AH. Coefficient de dissociation a = [A-]/
c de l'aspirine dans la solution S puis dans le liquide gastrique et [AH]+[A-] = c ; [A-](1+ [AH]/[A-]) = c ; [A-] / c = (1+ [AH]/[A-])-1. solution S : log ([A-]/[AH]) = 2,65 -3,5 = - 0,85 ; [A-]/[AH] =0,141 ; [AH]/[A-]= 1/0,141 = 7,1 [A-](1+7,1) = c ; [A-]/c = 1/8,1 = 0,23. suc gastrique : log ([A-]/[AH]) = 1,5 -3,5 = - 2 ; [A-]/[AH] =0,01 ; [AH]/[A-]= 1/0,01 = 100 [A-](1+100) = c ; [A-]/c
= 1/101 = 0,01.
Le pH de la solution d'aspirine effervescente est peu acide ( pas de brûlure d'estomac) ; la dissolution du comprimé est plus facile : le dégagement gazeux disperse de petits fragements du comprimé en solution. HCO3- + AH = CO2
+ A-+H2O CO2 + 2H2O = HCO3- + H3O+ avec Ka1 = 10-6,35 = [HCO3-][H3O+]/ [CO2] AH +H2O = A- + H3O+ avec Ka= 3,2 10-4 =[A-] [H3O+] / [AH ] K=Ka / Ka1 = 3,2 10-4
/ 10-6,35 = 3,2 10-4 /
4,47 10-7 = 716.
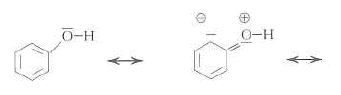
formes mésomères réaction acide base : F-OH + HO- = F-O- + H2O L'action du dioxyde de carbone sur le
phénate de sodium conduit au salicylate de sodium de formule C7H5O2Na
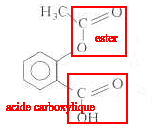
: réaction de substitution électrophyle salicylate de sodium + H3O+ = acide salicylique + H2O ou A- + H3O+ = AH + H2O K= [AH]/ ([A-][ H3O+])= 1/Ka = 1/10-3 = 1000, valeur grande, donc réaction totale. acide salicylique +( CH3-CO)2O= aspirine + CH3-COOH. L'acide sulfurique est un catalyseur ;
avec l'anhydride éthanoïque, la réaction est totale ; avec l'acide
éthanoïque elle est limitée par l'hydrolyse de l'ester.
acide salicylique : C7H6O3 : 138 g/mol ; 4,7 / 138 = 3,4 10-2 mol. anhydride éthanoïque : ( CH3-CO)2O : M= 102 g/mol ; 5,4 / 102 = 5,3 10-2 mol ( en excès) On recristallise le solide afin de le purifier : dissoudre le solide à chaud dans le volume minimum de solvant, puis laisser refroidir : le solide cristallise à froid. Quantité théorique d'aspirine (M= 180
g/mol) : 3,4 10-2 mol soit 3,4 10-2*180 = 6,12 g
|
||||
|
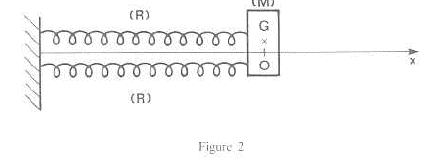
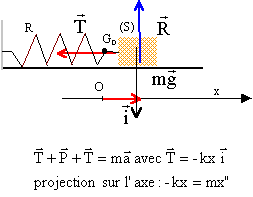
Un pendule horizontal est constitué d'un ressort (R), de masse négligeable, de raideur k et d'un solide (M) de masse m. L'une des extrémités de (R) est liée à (M), l'autre à une paroi fixe. (M) évolue sur une table à coussin d'air horizontale. On néglige les frottements. On écarte (M) vers la droite ; lorsque G a une abscisse a, on abandonne (M)sans vitesse initiale. 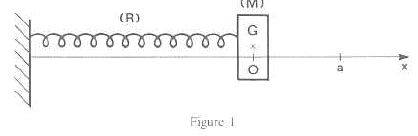
corrigé Equation différentielle du mouvement faisant intervenir l'abscisse x de G et x":
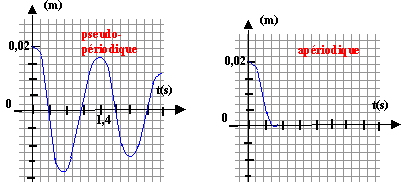
ou encore x"+k/m x=0 ; en posant w²= k/m = 2/0,1 =20 ; w= 4,47 rad/s ; T= 2p / w= 6,28 / 4,47 = 1,40 s. x"+ w²x=0 ; équation horaire du type x(t) = a cos (wt) = 0,02 cos(4,47 t). Le ressort (R) est remplacé par un ensemble de deux ressorts, ayant chacun les mêmes caractéristiques que (R). L'association est équivalente à un ressort unique de raideur 2k. d'où la nouvelle période : T' = 2p(m/(2k))½=6,28
(0,1/4)½= 0,993 s.
kg m s-2 m-1 s : h s'exprime en kg s-1. à l'expression précédente x"+k/m x=0 on ajoute à gauche +hv soit hx' x"+h x' +k/m x=0 h²-4k/m <0 soit h² < 4k/m ; h<2(k/m)½ ; h <8,94 kg s-1.
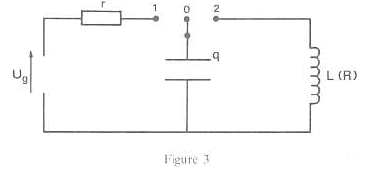
ug= r i + q/C avec i = dq/dt = q' ; ug= rq' + q/C ; q' +1/(rC) q= ug. On pose rC= t = 104*2 10-6
= 0,02 s; q' +1/t q= ug ; q'+1/0,02 q= 6 ; q' + 50 q= 6. q(t= 5t) = 6(1-exp(-50*5*0,02)) = 6(1-exp(-5) )= 5,96 V La charge du condensateur est pratiquement terminée lorsque t =5 t . Equation différentielle du circuit faisant intervenir q et q"= d²q/dt²: q/C= Ldi/dt avec i = -dq/dt ( décharge) soit di/dt = - d²q/dt² = -q" q/C= -Lq" ; q/C+Lq"=0 ; q"+1/(LC)q=0 ; w²= (LC)-1 = (1*2 10-6)-1=
5 105 ; w= 707 rad/s ; T= 2p / w= 6,28 / 707 =
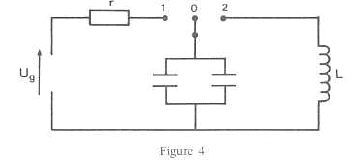
8,89 10-3 s. On reprend la série d'expériences ci-dessus en remplaçant le condensateur par l'association en parallèle de deux condensateurs chacun de capacité C : le condensateur équivalent a une capacité égale à 2C. Nouvelle période de l'oscillateur : 2p (2LC)½ = 6,28 ( 4 10-6)½ = 1,26 10-2 s. Oscillations électriques amorties : Equation différentielle reliant q, q' et q". ajouter Ri = -Rq' à droite de l'expression q/C= Ldi/dt +Ri q/C+Rq'+Lq"=0 ; q"+ R/L q' +
q(LC)=0. (R/L)²-4/(LC) <0 soit R² < 4L/ C; h<2(L/C)½ ; R <1,41 kW.
|
||||
|
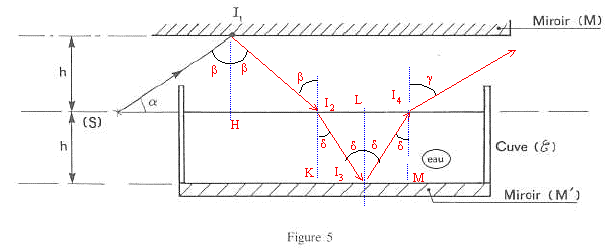
A optique géomètrique : la source ponctuelle (S) émet un pinceau de lumière monochromatique assimilable à un rayon SI1. Ce rayon fait un angle a avec l'horizontale. Le rayon se réfléchi en I1 sur le miroir horizontal (M). Après réflexion en I1, le rayon lumineux frappe en I2, la surface libre de l'eau contenue dans la cuve. Cette cuve possède un fond horizontal recouvert d'un miroir (M'). Le plan horizontal contenant la source (S) et la surface libre de l'eau contenue dans la cuve est à égale distance des plans horizontaux contenant respectivement le miroir (M) et le miroir (M'). 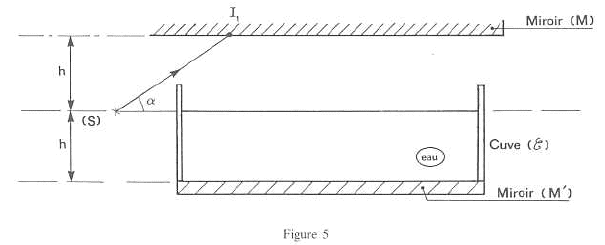 h= 10 cm ; a= 30 ° ; indice de l'eau par rapport à l'air : n = 1,33.
B optique ondulatoire :
corrigé Lois de Descartes relatives à la réflexion et à la réfraction. rayons incident, réfléchi et réfracté sont dans un même plan angle d'incidence = angle de réfraction ; n1 sin i1 = n2 sin i2.
Expression de SI2 en fonction de h et a : SI2 = 2 SH ; tan a =h/ SH ; SI2 = 2h/ tan a ; SI2 =2*0,1 /tan30 = 0,346 m. L'énergie lumineuse incidente en I2 est en partie réfléchie dans l'air et en partie transmise à l'eau. Expression de SI4 en fonction de h, n et a : SI4 = SI2 +2 LI2 ; tan d = LI2 /h ; SI4 = SI2 +2h tan d = 2h/ tan a + 2h sin d / (1-sin²d)½ ; sin b = sin ((½p-a) = cos a = n sin d ; sin d = cos a / n SI4 = 2h / tan a + 2h cos a /(n²-cos²a)½ ; SI4= 0,2[1/tan30+
cos30/(1,33²-cos²30)½= 0,517
m.
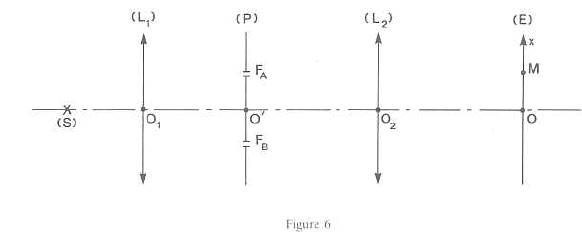
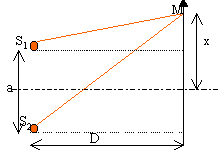
Phénomène optique produit par ces fentes : diffraction ( dans la mesure où la largeur des fentes est du même ordre de grandeur que la longueur d'onde de la lumière) Chemin optique : chemin parcouru par la lumière dans le vide pendant la durée de propagation dans le milieu considéré.
différence de marche d = n(S1M-S2M) . Tout le système est plongé dans le même milieu d'indice n=1. On supposera D >> a soit S1M + S2M voisin 2 D. S1M²=D²+(x-0,5 a)² S2M²=D²+(x+0,5 a)² S2M² -S1M² = (x+0,5 a)²-(x-0,5 a)² (S2M-S1M)(S1M+S2M) = 2 a x S2M-S1M voisin a x /D d = a x /D avec D= f2. aspect de l'écran E : dans la région où se superposent les ondes, l'intensité lumineuse passe par des maximums et des minimums qui peuvent être nuls. Les maximums dépassent la somme des intensités des faisceaux pris séparément. Interfrange i = l f2 /a = 0,5 10-6 * 0,5 / 5 10-4 = 5 10-4 m.
|
||||
|
|