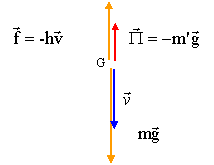|
d'après concours manipulateur radio Nantes 05. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
A. Chimie : L'iode est utilisée comme antiseptique en solution sous forme de I3-(aq) : c'est la teinture d'iode connue sous le nom de Bétadine. Une solution de 125 mL contient 5,0 g de I2.
Données :couples I3- /I- ; S4O62-/S2O32- ; M( I) = 126,9 g/mol. B. Physique : la glande thyroïde produit des hormones essentielles à différentes fonctions de l'organisme à partir de l'iode alimentaire. Pour vérifier la forme et le fonctionnement de cette glande, on procède à une scintigraphie thyroïdienne en utilisant les isotopes 13153I et 12353I de l'iode. Pour cette scintigraphie un patient ingère une masse m= 1,10 mg de l'isotope 13153I. masse molaire de l'isotope 13153I : M= 131 g/mol; NA= 6,02 1023 mol-1 ; antimoine Sb ( Z= 51) ; tellure Te (Z=52) ; Xenon Xe (Z=54) ; césium Cs ( Z= 55)
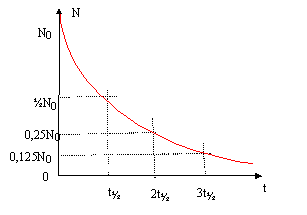
corrigé 13153I représente le noyau d'iode 131 ; ce noyau compte 53 protons et 131-53 = 78 neutrons 53I : le numéro atomique de l'élément iode est 53 ( soit 53 électrons dans l'atome d'iode) Qté de matière diiode (mol) = masse (g) / masse molaire diiode (g/mol) = 5 / (126,9*2)= 1,97 10-2 mol concnetration (mol/L) c0= Qté de matière (mol) / volume solution (L) = 1,97 10-2 / 0,125 = 0,158 mol/L. I3- + 2e- = 3I- réduction du diiode 2S2O32- = S4O62-+ 2e- oxydation de l'ion thiosulfate 2S2O32- + I3- = 3I- + S4O62- oxydo réduction à l'équivalence du titrage, les quantités de matière des réactifs sont en proportions stoéchiomètriques. n(I3-)= ½ n (S2O32-) ; C0V0 = ½ C1VE. nombre d'atomes N0 radioactifs initialement présents : Qté de matière (mol) = masse (g) / masse molaire (g/mol) = 1,1 10-6 / 131 = 8,4 10-9 mol Dans une mole d'atome il y a NA= 6,02 1023 atomes ; N0 = 8,4 10-9*6,02 1023=5,05 1015 atomes. 13153 I = AZ X* + 0-1e conservation de la charge : 53= Z-1 soit Z= 54 et X est le Xénon conservation du nombre de nucléons : 131 = A +0 soit A= 131. 13154 Xe* = 13154 Xe + 00g. le noyau fils peut se trouver dans un état excité ; il libère de l'énergie sous forme de photon g en revenant à l'état fondamental , de moindre énergie, état le plus stable. demi-vie d'un échantillon radioactif : durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintégrés. N(t) = N0 exp(-lt) ; et N( t½) = ½N0. ½N0= N0 exp(-lt½) ; ½= exp(-lt½) ; ln ½ = - lt½ ; ln2 = lt½.
activité A0 = l N0 avec l = ln2 / t½ = ln2 / (8*24*3600)=10-6 s-1. A0 = 10-6* 5,05 1015 = 5,05 109 Bq. A ( t= 4 h) = A0 exp(-4l) avec l = ln2/ (8*24)=3,61 10-3 heure-1. A ( t= 4 h) = 5,05 109 exp(-4*3,61 10-3)=4,98 109 Bq. cas de l'isotope 123 de l'iode : t½ = 13,2 h ; l = ln2/ 13,2 = 5,25 10-2 heure-1. A(t) = 4,98 109 Bq ; A0 = 5,05 109 Bq ; ln(A0 /A(t))= lt ; t= 1/l ln(A0 /A(t))= 1/ 5,25 10-2 ln( 5,05/4,98)= 0,266 heure = 16 min.
|
||||||||||||||||||||||||
|
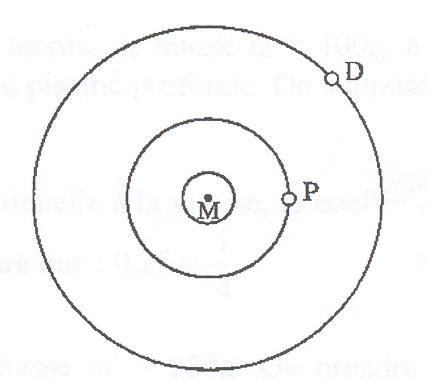
Sous deux aspects au moins Mars est très semblalble àla terre. Tout d'abord elle tourne autour de son axe en 24 h 37 min, ce qui fixe le jour martien à 41 min à peine de plus que le jour terrien. Son axe est incliné de presque 25 ° sur le plan de son orbite (1), soit 1,5° de plus que l'axe de la Terre. Aussi, comme la terre , Mars est soumise à un cycle régulier de saisons. Les deux satellites de mars, Phobos et déeimos, ont été découverts par Asaph Hall. Phobos est un bloc de rocher allongé creusé de cratères. Son diamètre maximum ne dépasse pas 25 km. Il orbite si près de la planète ( 6000 km)(2) qu'il se lève et se couche deux fois par jour martien (3). Deimos est trois fois plus éloigné de Mars et encore plus petit que Phobos, son diamètre n'excédant pas 6 km. (1) 25° est l'angle entre l'axe de mars et la normale au plan de son orbite. (2) 6000 km représente l'altitude du centre de Phobos par rapport au sol martien. (3) Phobos tourne sur son orbite dans le même sens que Mars autour de son axe. G= 6,67 10-11 SI Mars : période de rotation propre autour de l'axe des pôles TM= 24 h 37 min ; rayon de la planète RM= 3400 km ; masse MM. Phobos : période de révolution autour de Mars TP= 7 h 39 min 14 s ; rayon de l'orbite marsocentrique RP.
C'est un référentiel par rapport auquel le Principe de l'inertie est vérifié. Principe de l’inertie : Dans un référentiel Galiléen, si la somme des forces extérieures appliquées à un système est nulle alors le centre d’inertie de ce système est, soit au repos, soit en mouvement rectiligne uniforme.
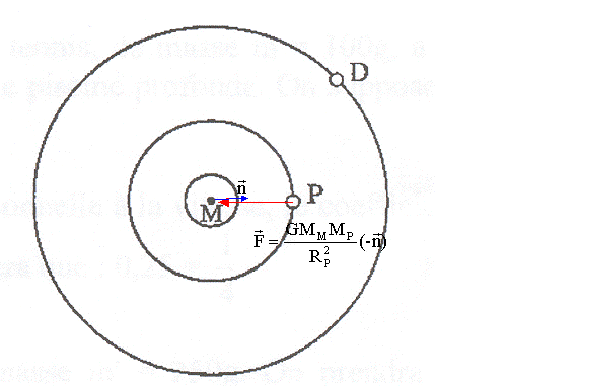
G constante de gravitation universelle (kg-1 m3 s-2); F force (newton) ; MM : maasse de Mars (kg) MP :masse de Phobos (kg) ; RP rayon de l'orbite de Phobos (m). Première loi ou loi des orbites : dans le référentiel héliocentrique, l'orbite de chaque planète est une ellipse dont l'un des foyers est le centre du soleil. Deuxième loi ou loi des aires : le mouvement de chaque planète est tel que le segment de droite reliant le soleil et la planète balaie des aires égales pendant des durées égales. Troisième loi ou loi des aires : pour toute les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la période est le même. vitesse de Phobos sur son orbite : Phobos est soumis à la seule force de gravitation F= G MMMP/R²P ; le mouvement est circulaire uniforme, donc l'accélération est centripète. La seconde loi de Newton s'écrit suivant l'axe n de la base de Frenet : F=MPv²/RP G MMMP/R²P = MPv²/RP soit v=[GMM/RP]½. période TP de Phobos sur son orbite : Phobos décrit, à la vitesse v, une circonférence de rayon RP en TP seconde 2pRP= vTP soit 4p2R2P= v2T2P remplacer v² par G MMRP : 4p2R2P= G MM/RP T2P 4p2R3P=G MMT2P soit MM = 4p2R3P/(GT2P). RP= (3400+6000)103 m = 9,4 106 m ; TP= 7*3600+39*60+14= 2,76 104 s. MM= 4*3,14²*(9,4 106)3/(6,67 10-11 * (2,76 104)²)=6,5 1023 kg. Phobos et Deimos ne s'écrasent pas sur Mars en raison de leur vitesse qui n'a pas ou peu changée depuis qu'ils sont en orbite. En effet, ils tournent suffisamment vite pour ne pas "tomber", et comme il n'y a pas de frottement (donc de déperdition d'énergie) dans l'espace, ils conservent leur vitesse. La force gravitationnelle exercée par Mars sur ces deux satellites a pour effet de maintenir ces deux satellites sur une trajectoire circulaire; en absence de cette force il s'éloigneraient de Mars suivant un mouvement rectiligne uniforme ( principe d'inertie)
|
|||||||||||||||||||||||||
|
Un fusil spécial peut envoyer des balles, de type balles de tennis, de masse m= 100 g à la vitesse v0= 24 m/s. On tire verticalement vers le bas, vers l'eau d'une piscine profonde. On supposera que la balle pénètre dans l'eau à l'instant t=0 avec la vitesse v0. Dans l'eau la balle subit une force de frottement proportionnelle à la vitesse, le coefficient de proportionnalité est h= 0,25 unité SI. Un volume d'eau égal à celui de la balle aurait une masse m'=250 g. On prendra g= 10 m/s². On ne considèrera que le mouvement de la balle dans l'eau, l'axe de celui-ci étant orienté vers le bas.
corrigé La balle, dans l'eau, est soumise à son poids, vertical vers le bas, valeur mg, à la poussée d'Archimède, verticale vers le haut valeur m'g et à la force de frottement , verticale vers le haut valeur f= hv.
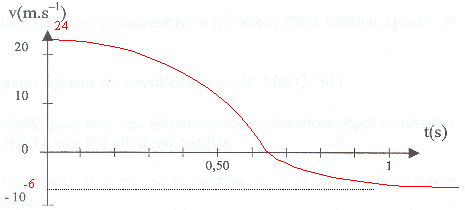
La seconde loi de Newton s'écrit, suivant un axe vertical orienté vers le bas : mg-m'g-hv= mdv/dt m dv/dt + hv = (m-m')g expression de la vitesse limite vl dans l'eau : dvl/dt=0 soit hvl= (m-m')g ; vl= (m-m')g/h vl=(0,1-0,25)*10/0,25 = -6 m/s. le signe moins signifie que la vitesse est orientée en sens contraire de l'axe ; la balle remonte et se dirige vers la surface. temps t caractéristique du mouvement : t = m/h = 0,1 / 0,25 = 0,4 s. la balle se remet à remonter lorsque la vitesse s'annule. v=0 = v0 exp(-h/mt ) + g(m-m')/h (1- exp(-h/mt )) 0= 24 exp(-2,5t) -6(1-exp(-2,5t)= 30 exp(-2,5t) -6 exp(-2,5t) = 6/30 = 0,2 ; -2,5 t = ln(0,2) ; t = 0,64 s.
|
|||||||||||||||||||||||||
|
On désire connaître la concentration molaire c0 d'une solution de permanganate de potassium. L'ion permanganate est l'oxydant du couple MnO4-/Mn2+. On prépare pour cela une solution incolore d'acide oxalique en dissolvant 5,0 g du solide cristallisé C2H2O4,2H2O dans 100 mL d'eau distillée. On titre ensuite 10 mL de la solution de permanganate de potassium par la solution d'acide oxalique acidifiée.
corrigé 5 fois {C2H2O4 = 2 CO2+ 2e- + 2H+} 2 fois { MnO4-+ 5e- + 8H+ = Mn2+ + 4 H2O} 5C2H2O4 + 2MnO4-+6H+ =10 CO2+ 2Mn2+ + 8 H2O M[C2H2O4,2H2O]= 2*12+2+4*16+2*18=126 g/mol Qté de matière (mol) = masse (g) / masse molaire (g/mol) = 5/126 =3,97 10-2 mol concentration c1 (mol/L= Qté de matière (mol) / volume de la solution (L) =3,97 10-2/0,1 =0,397 mol/L. l'ion permanganate, la seule espèce
colorée, sert d'oxydant et d'indicateur de fin de réaction : avant
l'équivalence MnO4- est en excès (couleur
violette); après l'équivalence MnO4- est en
défaut ( solution incolore)
0,397*12 10-3 = 4,76 10-3 mol 10-2C0 -2xéqui=0 ;C0
= 200xéqui=200*9,53 10-4 =0,19
mol/L.
|
|||||||||||||||||||||||||
|
|