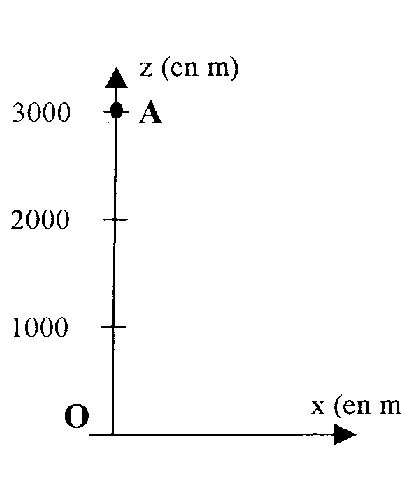Aurélie juin 05

Le radon ; circuit RC et circuit RL ; saut en parachute.

d'après concours entrée orthoptie Montpellier 05.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


radioactivité
  1.  Quelle est la composition du noyau de l'isotope du radon 22286Rn.
  2. Cet isotope se désintègre spontanément en émettant des particules a. Ecrire l'équation de la réaction de cette désintégration.
    Z
    83
    84
    85
    86
    87
    88
    89
    symbol
    Bi
    Po
    At
    Rn
    Fr
    Ra
    Ac

    nom

    bismuth

    polonium

    astate

    radon

    francium

    radium

    actinium
  3. Le radon est naturellement à l'état gazeux. A l'aide d'un appareil on mesure sur un échantillon d'air contenant du radon 222 un nombre n d'événements proportionnel au nombre de noyaux désintégrés. On répète l'opération 20 fois afin de dégager une moyenne ( La durée de l'expérience est suffisamment courte pour que l'activité du raddon ne diminue pratiquement pas)
    mesure
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    n
    5
    8
    9
    1
    12
    8
    14
    9
    12
    4
    9
    8
    6
    9
    10
    4
    9
    8
    10
    6
    Calculer la moyenne.
  4. L'activité moyenne est proportionnelle à la moyenne ci-dessus. Pour cette appareil Amoy= 80 nmoy, en Bq m-3. Calculer Amoy.
  5. Pour déterminer la demi-vie du radon 222, on reproduit les mêmes opérations que précédemment sur une période longue. Les mesures sont effectuées toutes les 50 heures.On trace la courbe ln Amoy = f(t)

     Rappeler la loi de décroissance radioactive. En admettant qu'elle s'applique à l'activité moyenne , justifier l'allure de la courbe ci-dessus.
  6. En utilisant les valeurs lues sur le graphe, déterminer la valeur de la constante radioactive l du raddon 222.
  7. Définir la demi-vie t½ du radon 222 ?
  8. Calculer la demi-vie du radon 222 ( en heures). 
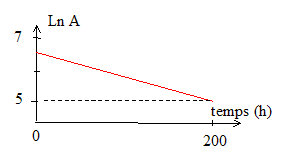
corrigé
composition du noyau de l'isotope du radon 22286Rn:

86 protons et 222-86=136 neutrons

22286Rn -->AZX+42He

conservation de la charge : 86=Z+2 soit Z= 84 et X est identifié avec le polonium

conservation du nombre de nucléons : 222=A+4 soit A= 218.

Faire la somme des n et diviser par le nombre de mesures : nmoy, = 8.

L'activité moyenne est proportionnelle à la moyenne ci-dessus. Amoy= 80 *8= 640 Bq m-3.

loi de décroissance radioactive : A(t)=A0 exp(-lt)

lnA= ln A0 -lt.

en représentant ln A en fonction du temps on obtient une droite de coefficient directeur -l et d'ordonnée à l'origine lnA0.

valeur de la constante radioactive l du raddon 222 = valeur absolue du coefficient directeur de la droite :

l=(6,5-5)/200 = 7,5 10-3 heure-1.

la demi-vie t½ : durée au bout de laquelle l'activité initiale est divisée par 2.

ln2 = lt½ soit t½ = ln2 / l= 92 h.

Partie A Etude d'un circuit RC

 

 

  1. Un circuit est constitué d'un générateur, d'un condensateur de capacité C =470 mF et d'un résistor de résistance R=50 W. On ferme K1, K2 restant ouvert. La figure ci-dessous permet de visualiser la tension aux bornes du condensateur pendant cette phase.

    Utiliser le document pour trouver la constante de temps t du circuit.

  2. Calculer la valeur maximale Wmax de l'énergie du condensateur.
  3. Le condensateur étant chargé on ouvre K1 puis on ferme K2 à la date t=0. La tension aux bornes du condensateur varie alors selon la loi : uc(t)= A exp(-t/(RC)). Déterminer la valeur de la constante A.
  4. Quelle relation lie l'intensité i(t) du courant et la charge q(t) du condensateur ?
  5. Quelle relation lie la tension uc(t) et la charge q(t)
  6. En déduire que i(t) est de la forme i(t) = B exp(-t/(RC)) où B est une constante que l'on exprimera en fonction des autres constantes.
  7. Calculer la valeur maximale de l'intensité pendant la décharge du condensateur. Dépend-elle de la capacité du condensateur ?

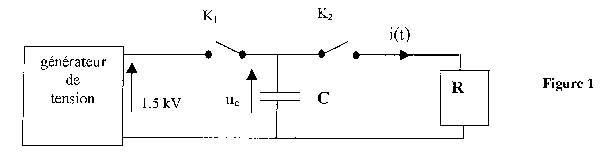
Partie B Etude d'un circuit LC

On réalise le circuit de la figure ci-dessous. Il comprend un générateur basses fréquences, une bobine de résistance r et une résistance R'= 10 kW montées en série. Le générateur délivre une tension en dents de scie de fréquence 1 kHz.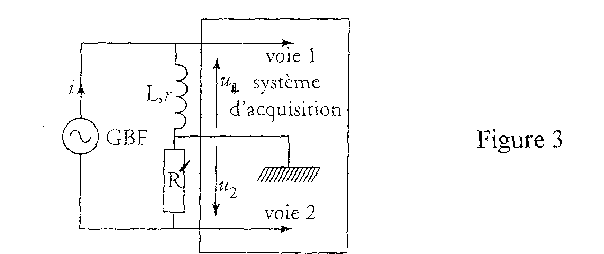

Un dispositif permet de visualiser sur un écran d'ordinateur la tension uL(t) aux bornes de la bobine et l'intensité i(t) du courant dans le circuit (figure4).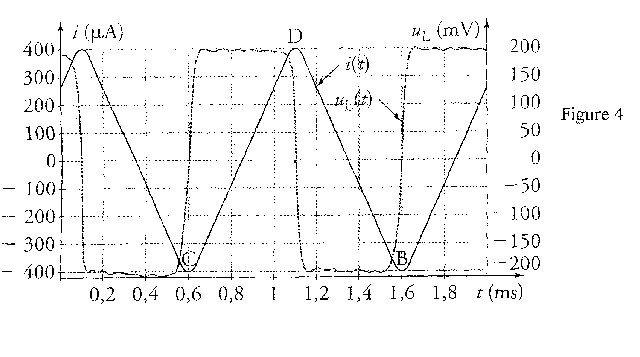

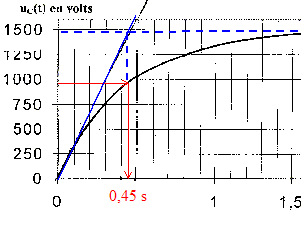
  1. Quelle est l'expression de la tension mesurée sur la voie 2 du dispositif ?
  2. Exprimer la tension uL(t) en fonction des caractéristiques de la bobine, du courant i et de sa dérivée.
  3. Que devient la tension uL quand l'intensité passe par un extrémum ?
  4. En mesurant sur la figure 4 la valeur de UL quand l'intensité passe par un extrémum, montrer que r est négligeable devant R'.
  5. En négligeant le terme faisant intervenir r et en utilisant les valeurs de la figure 4 entre les points C et D, calculer la valeur de L.

corrigé
constante de temps t du circuit :

à t= t la tension aux bornes du condensateur vaut 63% de sa valeur finale soit 1500*0,63 = 945 V

lecture graphe t= 0,45 s

ou bien abscisse de l'intersection de la tangente à l'origine avec l'asymptote horizontale.

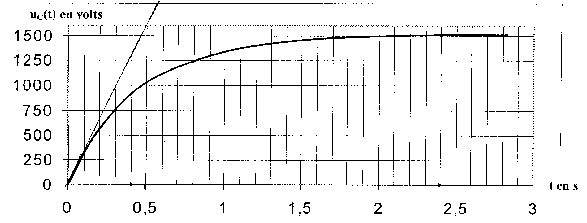
valeur maximale Wmax de l'énergie du condensateur :

E= ½CU²max = 0,5*470 10-6*1500² = 529 J.

uc(t)= A exp(-t/(RC))

à t=0 le condensateur n'a pas eu le temps de se décharger et la tension à ses bornes vaut 1500 V

1500 = A e0 soit A= 1500 V.

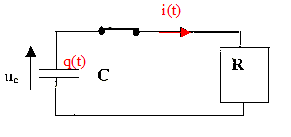
relation liant l'intensité i(t) du courant et la charge q(t) du condensateur : i(t) = - dq(t)/dt

relation liant la tension uc(t) et la charge q(t) : q(t) = Cuc(t)

soit Cduc(t)/dt = dq(t)/dt=-i(t)

équation différentielle relative à la charge : uc(t) = Ri(t)

q(t) / C=R(- dq(t)/dt) soit q(t) + RCdq(t)/dt=0

solution de cette équation q(t) = q0 exp(-t/(RC)) avec q0=CUmax, charge initiale

d'où en dérivant : dq(t)/dt = -CUmax /(RC)exp(-t/(RC)) soit i(t) = Umax / R exp(-t/(RC))

B= Umax / R = imax ( en début de la décharge), indépendante de la capacité du condensateur

imax = 1500 / 50=30 A.

expression de la tension mesurée sur la voie 2 du dispositif : u2(t) = -Ri(t)

tension uL(t) en fonction des caractéristiques de la bobine, du courant i et de sa dérivée : uL(t) = Ldi(t)/dt + ri(t)

quand l'intensité passe par un extrémum, di(t)/dt change de signe et la tension uL change de signe ( si on peut négliger le terme ri(t) devant L di(t)/dt)

sur la figure la valeur de UL passe de 0,2 V à son opposé -0,2 Vquand l'intensité passe par un extrémum :

de plus R'imax = 104*400 10-6 = 4 V, valeur bien supérieure à 0,2 V donc que r est négligeable devant R'.

lecture graphe sur un intervalle de temps où l'intensité est croissante :

di/dt = 800 10-6 / 0,5 10-3 = 1,6 As-1.

uL=0,2 V = Ldi/dt = 1,6 L soit L= 0,2/1,6 = 0,12 H.

saut en parachute

La caféine

Au point A et à la date t=0 un parachutiste saute d'un avion alors que celui-ci vole horizontalement à la vitesse V0= 130 km/h et à l'altitude h0=3000 m. g=9,8 m/s². Le mouvement du parachutiste, assimilé à un point matériel, est repéré par rapport à deux axes Ox et Oz. L'axe Ox est parallèle et de même sens que la vitesse initiale V0.

  1. Le parachutiste étant considéré en chute libre quelles sont les coordonnées ax et az de son vecteur accélération ?
  2. Etablir les équations horaires x(t) et z(t)
  3. Etablir l'équation de sa trajectoire.
  4. A quelle date le parachutiste atteint-il l'altitude h1=1000 m ?
  5. Quelle est la vitesse correspondante v1 lorsqu'il atteint l'altitude h1 ?
  6. En réalité la vitesse atteinte est v'1= 55 m/s. Calculer la diminution de l'énergie mécanique du parachutiste entre le départ au point A et le point d'altitude h1. Sous quelle forme cette énergie est-elle transformée ?
  7. A l'altitude h1 le parachutiste ouvre son parachute. Sa masse totale est 90 kg et son mouvement peut être considéré comme vertical. On néglige la poussée d'Archimède. La force de frottement opposée à la vitesse a pour valeur F= ½Krv²; v étant la vitesse, K =38 une constante dépendant de la forme et de la superficie du parachute et r = 1,3 kg/m3 la masse volumique de l'air. Quelle est l'unité de K dans le système SI ?
  8. Donner une expression de l'équation différentielle du mouvement.
  9. Au cours de cette phase la vitesse diminue et se stabilise à une valeur v2. Calculer v2.
corrigé
référentiel terrestre supposé galiléen ; repère lié au sol ( voir figure) ; système étudié : le parachutiste supposé ponctuel.

le parachutiste est soumis uniquement à son poids , vertical, vers le bas, valeur mg. La seconde loi de Newton donne l'accélération

coordonnées de son vecteur accélération : ax =0 et az =-g

coordonnées de la vitesse initiale par rapport au sol : v0x=130/3,6 =36 m/s et v0z=0.

le vecteur vitesse est une primitive du vecteur accélération : vx(t) =v0x=36 m/s ;vz(t) =-gt=-9,8 t

le vecteur position est une primitive du vecteur vitesse : x= v0x t et y = -½gt²+h0 = -4,9t²+3000.

trajectoire : éliminer le temps entre ces deux équations : t = x/ v0x = t/36

y= -4,9 /36²x² +3000 ; y = -3,7 10-3 x²+3000.

 date à là laquelle le parachutiste atteint-il l'altitude h1 :

1000 = -4,9t² + 3000 s'écrit t²= 2000/4,9 = 408 soit t=20,2 s.

vitesse correspondante v1 lorsqu'il atteint l'altitude h1 :

vx=36m/s ; vy= -9,8*20,2 = - 198 m/s : v1= [v²x+v²y]½=(36²+198²)½ = 201 m/s.

diminution de l'énergie mécanique du parachutiste entre le départ au point A et le point d'altitude h1:

la variation d'énergie mécanique est due à la diminution de l'énergie cinétique :

½mv1²-½mv'1²= -0,5*90[55²-201²)= -1,7 106 J.

cette énergie est transformée sous forme de chaleur lors des frottements sur les couches d'air.

l'unité de K dans le système SI :

F= ½Krv²; s'écrit : K= 2 F/(rv²) : newton /( kg m-3 m²s-2)

soit kg m s-2/( kg m-3 m2s-2) soit kg m s-2/( kg m-1 s-2): K est en m².

équation différentielle du mouvement :

le parachutiste est soumis à son poids, vertical, vers le bas, valeur mg et à la force F verticale vers le bas, valeur ½Krv²;

la seconde loi de Newton s'écrit : mdv/dt = -mg + ½Krv²;

Au cours de cette phase la vitesse diminue et se stabilise à une valeur v2.

Lorsque la vitesse limite v2 est atteinte, le mouvement est rectiligne uniforme : mg =½Krv2²

v2= [2mg/(Kr) ]½= [2*90*9,8 / (38*1,3)]½=6m/s ou 6*3,6 = 21,5 km/h



retour -menu