|
oscillateur harmonique ; cellule photoélectrique ; bobine. d'après concours technicien météo 96. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
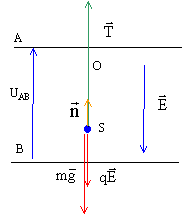
Une sphère conductrice S assimilable à un point matériel de masse m= 2 g et portant une charge q= 2 10-7 C, est suspendue en un point fixe O fixe par l'intermédiaire d'un fil isolant inextensible, de masse négligeable et de longueur L= 10 cm. Le pendule ainsi constitué est placé entre deux armatures métalliques A et B, planes et horizontales, de grandes dimensions, distantes entre elles de d= 20 cm. Le point de suspension O est situé à une distance a= 5 cm au dessus de l'armature supérieure A. On applique entre les armatures une différence de potentiel UAB= 2000 V, créant alors entre A et B un champ électrique uniforme E. g= 10 m/s². 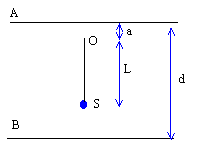
corrigé La sphère est soumise à son poids, à la tension du fil et à une force électrique.Le champ électrique E pointe vers le plus petit potentiel ; la charge q étant positive, force et champ électrique sont colinéaires et de même sens.
champ de pesanteur fictif : g1 = g + qE/m avec g=10 m/s² ; q= 2 10-7 C ; m = 2 10-3 kg ; E= UAB/d = 2000 / 0,2 = 104 V m-1. g1 = 10 + 2 10-7 *104 /2 10-3 = 11 m/s². période de ce pendule simple : T= 2p (L/g1)½
= 6,28 *(0,1/11)½ = 0,6 s.
Au passage à la position d'équilibre l'énergie est sous forme cinétique : Efin = ½mv² Cette énergie se conserve : mg1L =½mv² ; v² = 2g1L = 2*11*0,1 = 2,2 ; v= 1,48 m/s. Ecrire la seconde loi de Newton suivant l'axe n de la base de Frenet ; l'accélération est centripète aN= v²/L T- mg - qE = maN= mv²/L T= mg + qE + mv²/L= mg1+mv²/L
= m(g1+v²/L)=m(g1+2g1)=3mg1=
6 10-3*11= 6,6 10-2
N.
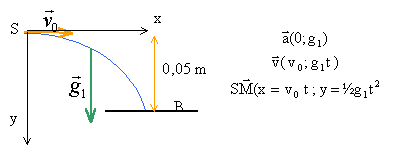
trajectoire : arc de parabole ; y=½g1x²/v0² la sphère touche l'armature B à la date t1 :t1²= 2y/g1= 0,1/11 =9,1 10-3 ; t1 = 9,5 10-2 s.
|
|
corrigé 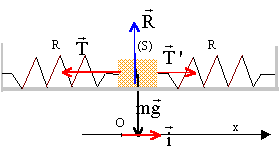
valeur de chaque tension T=T'=k(l-l0)= 13*(18-15)=13*0,03 =0,39 N. Le poids et l'action de la table se neutralisent. Ecrire la seconde loi de Newton sur l'axe O i : T'-T= mx" avec T'= k(l-x) et T= k(l+x) k(l-x) - k(l+x)= mx" ; -2kx = mx" ; mx"+2kx=0 ; x" + 2k/m x = 0 ; on pose w²= 2k/m ; on retrouve l'équation différentielle d'un oscillateur harmonique de période T0= 2p( m/ (2k)½. T0= 6,28 ( 0,65 / 26)½ =0,993 s. loi horaire du type : x(t) = xmax cos( w t+j) avec xmax = 0,02 m et w = (2k/m )½ = 6,32 rad/s. à t = 0 x(0) = 0,02 ; 0,02 = 0,02 cos j ; 1 = cos j soit j=0 x(t) = 0,02 cos( 6,32 t)
avec v = dx/dt = x' = 0,02*6,32(-1)sin(6,32t) = - 0,126 sin(6,32t) Ec = 0,5 * 0,65 (- 0,126 sin(6,32t)² = 5,2 10-3 sin²(6,32 t). l'énergie cinétique est maximale lorsque le mobile passe par la position d'équilibre ( l'énergie potentielle élastique est nulle) Ec max entraîne sin (6,32 t)=1 soit 6,32 t =p/2 = 1,57 ( p) t 1= 0,248 s = 0,25 T0; t n =
0,248 + np/6,32 avec n=1 , 2 , 3 ...
sin²(6,32 t) = 0,5 ; sin(6,32 t) = 0,707 6,32 t = 0,25 p + 2np et 6,32 t = p -0,25 p + 2np = 0,75 p + 2np t = 0,124 +0,994 n = T0/8 + n T0 et t =0,372 +0,994 n = 3T0/8 + n T0 ; abscisses correspondantes : x1 = 0,02 cos(6,32*0,124) = 0,014 m x1 = 0,02 cos(6,32*0,372) = -0,014
m ;
|
||
|
Une cellule photoélectrique constituée d'une surface métallique recouverte de césium est éclairée par un faisceau lumineux de longueur d'onde l=450nm. Un générateur permet de faire circuler les électrons émis par le métal et un microampéremètre mesure l'intensité du courant. Le travail d'extraction du césium est 1,88 eV.
h= 6,62 10-34 J s ; c= 3 108 m/s ; e= 1,6 10-19 J ; masse de l'électron m= 9,1 10-31 kg. corrigé travail d'extraction du césium: 1,88 eV = 1,88*1,6 10-19 = 3 10-19 J énergie du photon : E= hc/l0 =3 10-19 d'où l0 =hc/3 10-19=6,62 10-34*3 108/3 10-19= 6,62 10-7 m = 662 nm. vitesse avec laquelle l'électron est extrait de la cathode : énergie du photon incident : hc/l =6,62 10-34*3 108/ 450 10-9 =4,41 10-19 J cette énergie sert à extraire un électron ; l'excédent est emporté par l'électron sous forme d'énergie cinétique : Ec=½mv² = 4,41 10-19 -3 10-19 =1,41 10-19 J v²= 2*1,41 10-19 / 9,1 10-31
= 9,7 1011 ; v= 9,85 105
m/s.
photons reçus par le métal par seconde : P l /(hc) = 10-3 * 450 10-9 /(6,62 10-34*3 108)= 2,27 1015. rendement quantique : nombre électrons
émis / nombre photons reçus = 3,12 1013 /2,27 1015
= 1,15 10-2 = 1,15 %.
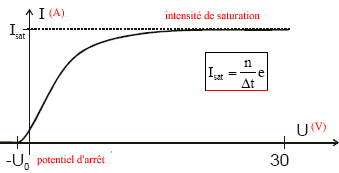
Si U augmente le nombre des électrons émis et qui atteignent le fil (qui circulent dans le circuit électrique) s'accroît. Si U est supérieure à une certaine valeur, tous les électrons émis par la plaque atteignent le fil. Il en résulte dans le circuit une intensité de saturation Isat où n est le nombre d'électrons émis pendant l’intervalle de temps D t et e = 1,6 10-19C, la charge élémentaire. si U < -U0, aucun électron n'atteint le fil. Plus la puissance lumineuse P reçue par
la plaque est importante, plus l'intensité du courant de saturation Isat
est grande. P n'a pas d'influence sur le potentiel d'arrêt U0.
Si la radiation a la longueur d'onde l <l0 , alors l'énergie des photons est suffisante pour extraire des électrons du métal . La puissance lumineuse reçue dépend du nombre N de photons frappant la plaque pendant l'intervalle de temps D t. Pour une lumière monochromatique de fréquence n. P= Nhn/D t = Nhc/(lD t) P étant constante si l diminue
alors N diminue et en conséquence le nombre d'électrons qui atteignent
l'anode est plus faible ( i va diminuer pour une tension U fixée)
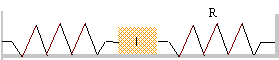
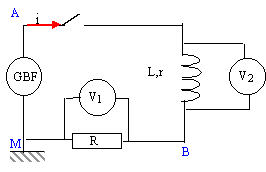
On réalise le circuit suivant : Le générateur délivre un courant alternatif de fréquence f= 50 Hz. La tension efficace aux bornes du générateur est Ueff= 20 V. R= 20 W. Les voltmètres V1 et V2 indiquent respectivement U1= 11,5 V et U2 = 11,2 V.
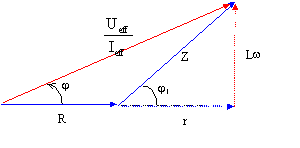
corrigé U1 eff = R Ieff soit Ieff =U1 eff / R = 11,5 / 20 =0,575 A. impédance Z de la bobine :U2 eff =Z Ieff soit Z=U2 eff / Ieff = 11,2 / 0,575 = 19,5 W.
Z²= r²+(Lw)²) avec w = 2pf= 314 rad/s. 19,5 ² = r² + 9,86 104 L² calcul de j : Ueff / Ieff =20 / 0,575 =34,8 W. Z² = 34,8² + R² - 2*34,8*R cos j ; cos j =(34,8² + R² -Z²) /(2*34,8*R) =0,884 soit j = 27,8°. de plus cos j = (R+r)/ 34,8 d'où R+r = 34,8 cos j =34,8*0,884 = 30,8 W soit r = 10,8 W. sin j = Lw/34,8 soit Lw= 34,8 sin 27,8 = 16,2 ; L= 16,2 / w = 16,2 / 314 = 5,1 10-2 H. La puissance est dissipée par les résistances: P= (R+r)I²eff = (20+10,8)*0,575²= 10,18 W.
|
||
| |
||
|
|